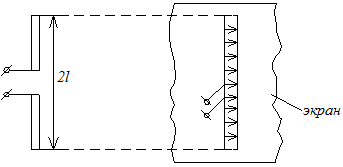
10. Симметричный щелевой вибратор.

Поле, созданное симметричной щелью, можно найти на основании принципа двойственности по аналогии с полем, созданным симметричным электрическим вибратором.

,

,

,

(5.2).

Учитывая, что первая антенна создает такое же поле, как и В, запишем выражения для поля, создаваемого щелью:

,

(5.3).

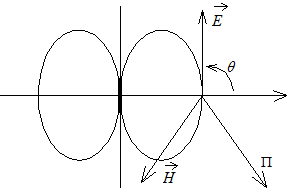
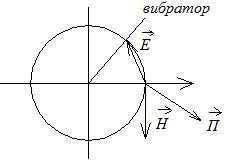
Сравнивая (2) и (3), видим, что ДН симметричного и щелевого вибратора будут совпадать.

,

.

• Симметричный вибратор

,

.

- Щелевой вибратор

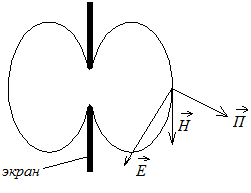
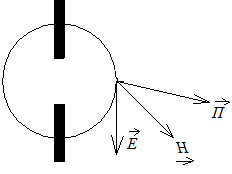
Входное сопротивление щели в точках питания определяется:

(5.4)

(5.5)

Для односторонней щели:

(5.6)

. Диапазонные свойства щелевого излучателя зависят от ширины щели и увеличиваются (улучшаются) с увеличением ширины щели.

11. Направленные свойства системы излучателей.

Для получения остронаправленных ДН в диапазоне КВ и низких частот УКВ применяются антенны, состоящие из большого числа идентичных излучателей. Хорошие направленные свойства, достигаемые при использовании таких систем, объясняются интерференцией полей, создаваемых отдельными излучателями.

В дальней зоне для отдельного излучателя напряженность поля можно представить в следующем виде:

(3.1),

где волновое число,

- действительная длина n-го излучателя,

- комплексная амплитуда тока в n-ом излучателе,

– ДН n-го излучателя,

r_n – расстояние от n-го излучателя до точки наблюдения.

Напряженность поля, создаваемая всей системой:

(3.2).

Будем рассматривать идентичные излучатели, одинаково ориентированные в пространстве. При этом векторным характером в выражении (3.2) можно пренебречь:

(3.2а),

,

,

, где – расстояние от центра системы излучателей до точки наблюдения (амплитудный сомножитель).

Подставим выражение (3.1) в выражение (3.2а):

(3.3),

где - величина постоянная для данной системы излучателей.

Предположим, что в выражении (2.37) (т. е. система состоит из ненаправленных излучателей). Тогда модуль выражения (2.37) будет определять направленные свойства такой системы:

(3.4).

Выражение (3.4) определяет множитель антенной системы.

Подставим выражение (3.4) в выражение (3.3).

Получим: .

Таким образом, ненаправленные свойства всей системы могут быть представлены в виде:

(3.5).

Выражение (2.39) определяет теорему перемножения ДН.

ДН из идентичных излучателей равна произведению ДН отдельного излучателя на множитель решетки.

9.1 Поле линейной системы идентичных излучателей (линейной антенной решетки).

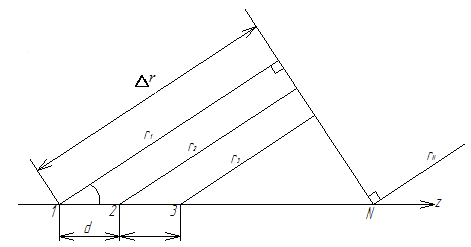
d – шаг решетки.

,

,

(3.6).

Подставим выражение (3.6) в выражение (3.3):

,

(3.7).

Выражение (3.7) показывает, что множитель линейной антенной решетки не зависит от угла .

Таким образом, у линейной антенной решетки направленные свойства проявляются только в плоскости, содержащей саму антенную решетку.

(3.8).

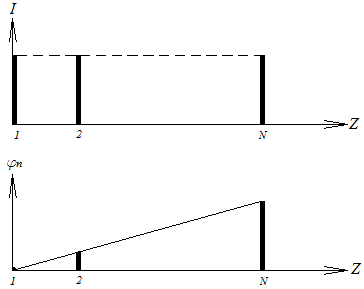
Это сумма первых членов геометрической прогрессии, у которой первый член равен 1, а .

,

(3.9)

,

где

,

– расстояние от центра антенной решетки до точки наблюдения,

фаза в центре антенной решетки.

Модуль выражения (2.43) определяет амплитудную характеристику антенной решетки. Фаза будет определять ФДН.

Фаза в точке наблюдения:

.

Таким образом, линейная антенная решетка является источником сферических волн с центром в середине решетки.

Множитель линейной решетки с линейным фазовым распределением согласно выражению (2.43) будет иметь вид:

(3.10),

, .

,

(3.11),

(3.12).

Анализируя графически выражения (3.10), (3.11) и (3.12), можно сказать, что множитель линейной антенной решетки имеет ряд максимумов.

Первый максимум, полученный при n=0 и m=0 называется главным максимумом. Все остальные максимумы называются вторичными или дифракционными.

Положение как главных, так и дифракционных максимумов зависит от величины (фазового набега тока между соседними излучателями).

Таким образом, регулировать величину можно, изменяя положение главного максимума, т. е. осуществить электрическое сканирование.

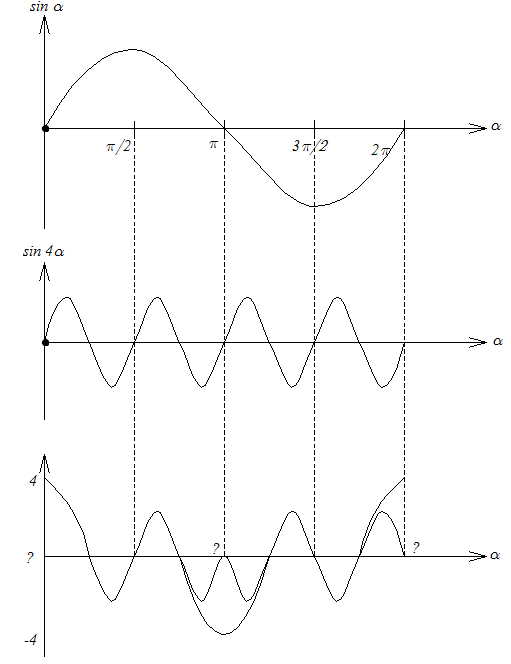
При одновременном выполнении условий (3.11) и (3.12) множитель решетки принимает значение, равное N (величина главного и дифракционного максимумов). Когда условие выполняется, а нет, множитель решетки . Это происходит, когда

1. Рассмотрим случай синфазного возбуждения излучателей, т.е. .

(3.13)

(3.14)

Если в выражении , т.е. – главный максимум.При синфазном излучении решётки, гл максимум решётки ориентирован перпендикулярно оси решётки.

Если , тогда - дифракционный максимум. (3.15) Положение 1го дифракционного максимума определяется соотношением

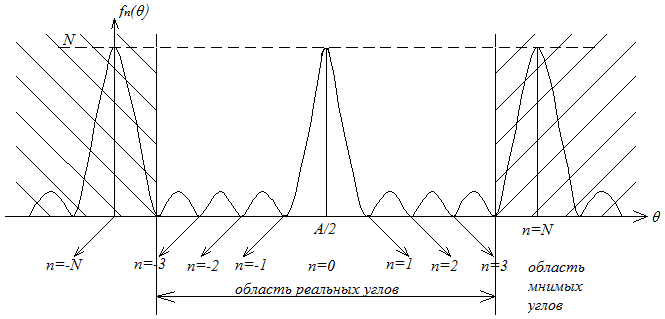
Пусть . Следовательно, не существует. Выражение определяет расположение первого дифракционного максимума. При этом он может располагаться как в области реальных углов ( ), так и в области мнимых углов ( ). Область расположения дифракционных максимумов зависит от соотношения λ к d. При синфазном возбуждении излучателей для того, чтобы первый дифракционный максимум находился в области мнимых углов, необходимо выполнение соотношения . (3.17)

2. Рассмотрим случай

Максимум числителя будет соответствовать условию , а максимум знаменателя . Одновременное выполнение этих условий будет обеспечивать появление максимума антенной решётки.

Главный максимум так же будет соответствовать условию m=0 n=0 . Из этого выражения следует, что менять напряжение главного максимума в антенных решётках, можно не перемещая саму решётку, а изменяя разность фаз между тонами в соседних излучателях. Этот процесс называется электронным сканированием.

В случае сканирования отсутствует дифракционный максимум в области реальных углов определяется более жестким условиям (его выполнением)