2.5. Основные топологические понятия и параметры эц

К топологическим (структурным) понятиям относят понятия ветви, узла и контура ЭЦ (ЭС).

Под ветвью понимают участок ЭЦ, где протекает один и тот же не разветвляющийся электрический ток. Простейшая ветвь состоит из одного элемента, сложная – из несколь­ких последовательно соединенных элементов. Количество ветвей в цепи является тополо­гическим или структурным параметром N_B . Виды ветвей в расчетной эквивалентной схеме зависят от выбранных схем замещения деталей. В учебных задачах мы будем в основном рассмат­ривать готовые расчетные эквивалентные схемы, а в практической работе может потребо­ваться самому составить расчетную эквивалентную схему.

Узел – это точка соединения трех и более проводников обязательно от каких-то элементов цепи. Точка соединения проводников от двух элементов называется устранимым узлом и обычно не учитывается. Устранимые узлы используются, когда надо детально описать расположение элементов, например, при компьютерных расчетах. На схемах в ряде слу­чаев показывают многоточечные узлы (между точками нет никаких элементов). Такой узел считается за один. Количество узлов является топологическим или структурным параметром цепи N_УЗ.

Под контуром понимают замкнутый путь, проходящий по элементам ЭЦ через ее ветви и узлы. В ряде случаев используют так называемый неявный проход через какие-то эле­менты, когда некоторые элементы обходятся более кратким путем. Структурным или топологическим параметром цепи является количество незави­симых контуров, где каждый последующий отличается от всех других хотя бы одним эле­ментом, одной ветвью и где все элементы охвачены контурами.

Существует структурная или топологическая формула для определения количества независимых контуров .

Для примера рассмотрим следующую схему:

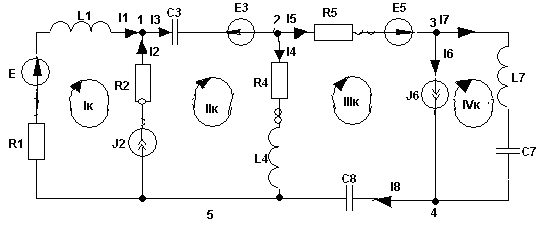
Здесь N_в=8 N_уз=5. 5 узел здесь двухточечный. N_нк=8-5+1=4 . Для простых схем число независимых контуров равно количеству различных замкнутых ячеек N_яч=4.

Направление обхода по контуру выбирается произвольно, но указывается на схеме и по­том не меняется. Здесь все проходы по контурам явные.

2.6. Законы Кирхгофа

Первый закон Кирхгофа – это физический закон баланса токов в узле, основан на том, что заряды в узле не накапливаются, а перемещаются по проводникам.

Формулировка: алгебраическая сумма мгновенных значений токов узла равна 0 в любой момент времени. Правило знаков: токи, направленные к узлу, берутся с одним знаком (+), от узла – с про­тивоположным (-). Для примера рассмотри схему

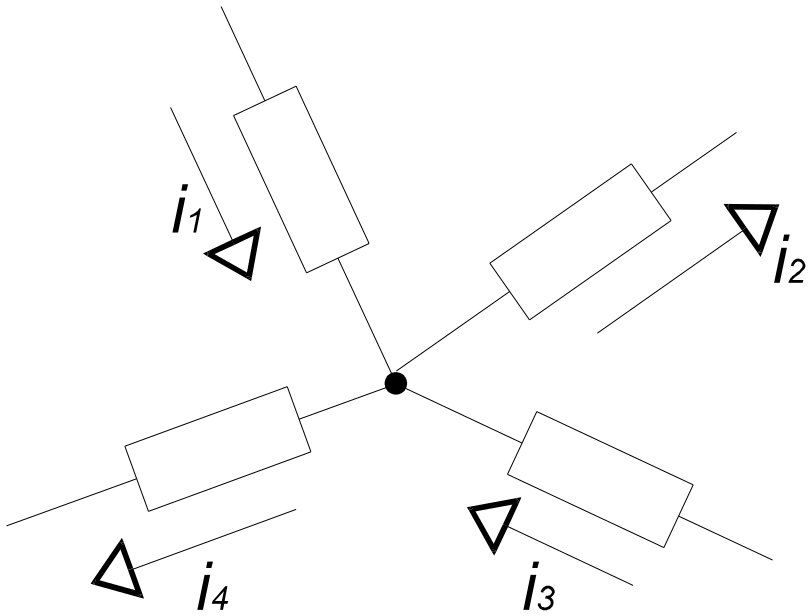i₁(t) - i₂(t) + i₃(t) - i₄(t) = 0

Если взять1 узел из схемы предыдущего параграфа то для первого узла в ней

i₁ + i₂ – i₃ = 0.

Е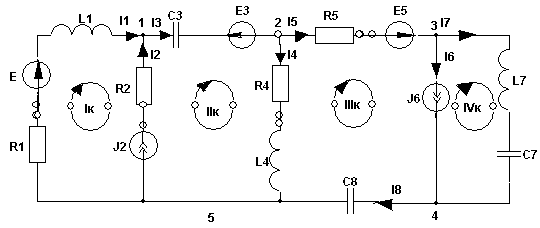 сть вторая формулировка: сумма подходящих к узлу токов равна сумме отходящих от узла токов для мгновенных значений.

i₁(t) + i₂(t) = i₃(t) (см. сх.)

Используется та запись, которая удобна в конкретном случае.

Для конкретной схемы можно составить столько уравнений, сколько узлов, но независи­мых уравнений на единицу меньше числа узлов. N_нуIзк=N_уз – 1 ( =4)

Второй закон Кирхгофа – это физический закон баланса напряжений в замкнутом кон­туре.

Формулировка: алгебраическая сумма мгновенных значений напряжений на элементах контура равна 0 в любой момент времени. Правило знаков: напряжения, совпадающие с обходом по контуру, берутся со знаком “+”, не совпадающие – со знаком “-”.

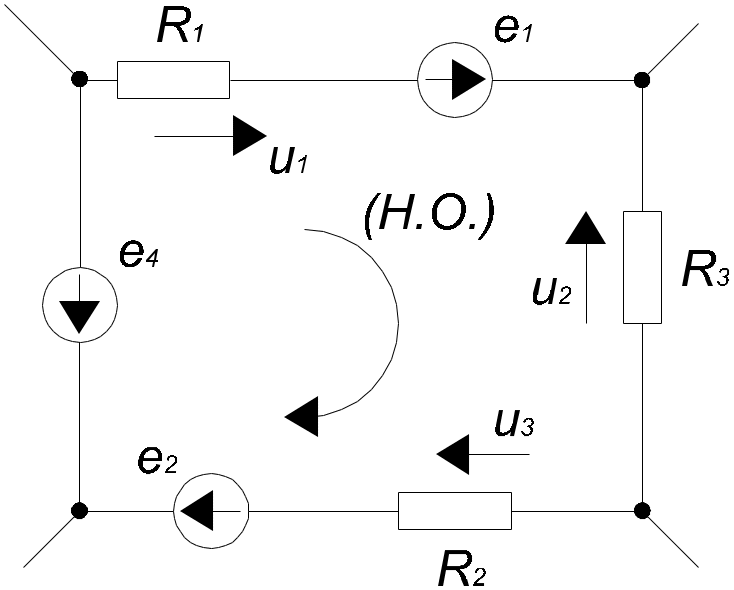
u₁- u_e1 - u₂ + u₃ -u _e2 +u _e4= 0 Напряжение на источнике ЭДС равняется ЭДС и направляется противоположно. Оно является обычно заданной величиной. Поэтому целесообразно такие напряжения переносить в правую часть уравнения.

u₁ - u₂ + u₃ = е₁ +е₂-е₄ В результате получается вторая формулировка (рабочая): алгебраическая сумма напряже­ний на элементах контура за исключением источников ЭДС равна алгебраической сумме ЭДС в этом контуре. Все справедливо для мгновенных значений.

Число независимых уравнений по II закону Кирхгофа равно числу независимых контуров. N_нуIIзк=N_нк=N_B-N_УЗ+1(=4) Для 1 контура большой схемы можно записать

u_R1 – u_e1 + u_L1 – u_R2 + u_j2 = 0 (напряжение на источнике тока взято противоположного направления относительно источника) . Можно переписать: u_R1 + u_L1 – u_R2 + u_j2 = e₁

В итоге для схемы электрической цепи можно составить целую систему уравнений, коли­чество которых N_нуIIзк + N_нуIзк = N_уз + N_нк – 1 = N_в. Если напряжения выразить через токи, то такая система может быть решена.