2. Основы мкт

В качестве неизвестных здесь используются так называемые контурные токи. Это некоторые условные мысленные токи, протекающие по выбранным независимым контурам. В качестве дополнительных неизвестных берутся напряжения на идеальных источниках тока. Система уравнений составляется только на основе второго закона Кирхгофа с применением закона Ома. Конкретные токи ветвей (действительные токи) определяются как алгебраическая сумма соответствующих контурных токов, протекающих через ветвь.

3. Определение числа уравнений и выбор контуров для мкт

Количество уравнений определяется по формуле:

Контуры выбираются так, чтобы в них не входили идеальные источники тока (основные контуры). Дополнительные контуры выбираются с одним источником тока. Их уравнения в систему не включаются, но их влияние учитывается при решении системы.

4. Пример использования

I1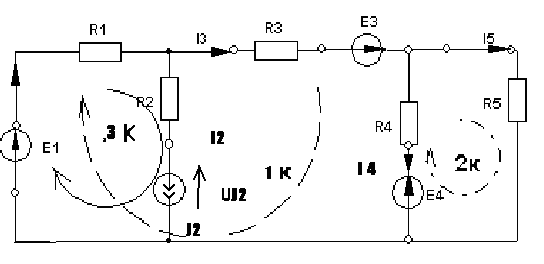

N_B=5, N_УЗ=3, N_HK=3, N_ИИТ(J)=1.

Выбираем 1 и 2 контуры без идеальных источников тока. Составляем систему уравнений для основных контуров (1 и 2), используя контурные токи I_1К,I_2К, причем I_3К=J₂..

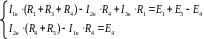
Решив данную систему и определив контурные токи, найдем токи ветвей следующим образом:

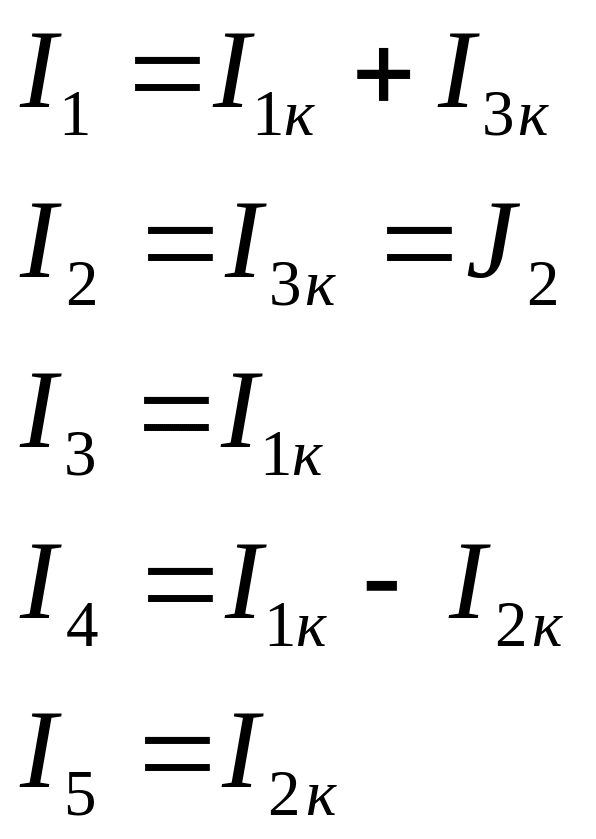
Для определения напряжения на источнике тока составляется вспомогательное уравнение по закону Кирхгофа для дополнительного (3) контура: . Отсюда определяется U_J2.

Можно выделить алгоритм расчета:

1. Определение количества уравнений

2. Выбор основных и дополнительных контуров

3. Составление системы уравнений для контурных токов

4. Решение системы уравнений

5. Определение токов ветвей

6. Определение напряжений на источниках тока.

5. Общая стандартная форма записи системы уравнений по МКТ

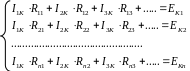
Записывают и в матричном виде для резистивных цепей с источниками постоянного действия

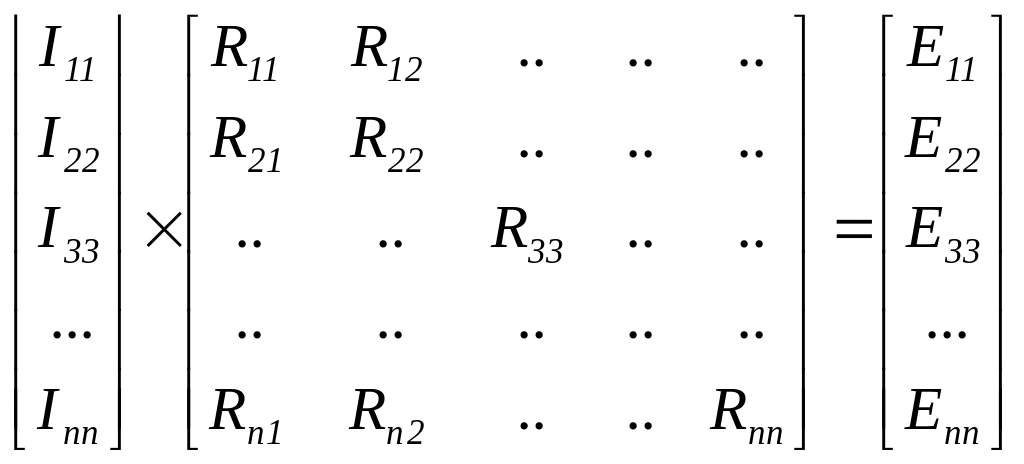
Здесь: I_nn (I_nK ) – соответствующие контурные токи,

R₁₁ –собственное контурное сопротивление первого контура, равное сумме сопротивлений элементов входящих в 1 контур, R₂₂ –контурное сопротивление второго и т.д.;

R₁₂ – взаимное сопротивление между первым и вторым контурами (учитывается с +, если контурные токи совпадают и с “- ”, если не совпадают) и аналогично;

E₁₁ – контурная ЭДС 1 контура, которая содержит алгебраическую сумму ЭДС входящих в 1-ый контур (c + если совпадает с контурным током) и включает влияние источников тока на контур (после переноса из левой части). Далее аналогично.

Причем обычно R₁₂ = R₂₁ а если есть управляемые источники, то R₁₂ и R₂₁ могут быть не равны.

6. Применение мкт

Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L- и C-элементы и частоты источников одинаковые, то применяется в комплексной форме. Если частоты действия разные, то можно применять совместно с методом наложения для расчета частичных токов.

§4. Метод узловых напряжений (мун)

1. Основы мун

В качестве основных неизвестных используются так называемые узловые напряжения – это напряжения между узлом схемы или цепи и некоторым опорным или базисным узлом, который выбирается один для всей цепи или схемы. В качестве дополнительных неизвестных используются токи в некоторых «вырожденных» ветвях, которые содержат только идеальные источники напряжения (или ЭДС) без других элементов.

Система уравнений по МУН составляется на основе первого закона Кирхгофа. Второй закон и закон Ома используются как вспомогательные.

2. Определение количества уравнений и выбор базисного узла

Количество уравнений определяется по формуле:

, где N_E – число «вырожденных» ветвей которые содержат только идеальные источники напряжения (или ЭДС) без других элементов.

Базисный узел выбирается из узлов, прилегающих к ветви «вырожденной» (где есть одиночный идеальный источник напряжения) и отмечается знаком заземления или корпуса.

I₁ E₁

1. Из этих двух узлов обычно берут тот узел, где больше подходит ветвей.

2. Берут там, где удобнее при взгляде на схему.

Начинается метод с определения числа «вырожденных» ветвей и базисного узла, потом составляется и решается система уравнений.

3.Пример применения МУН

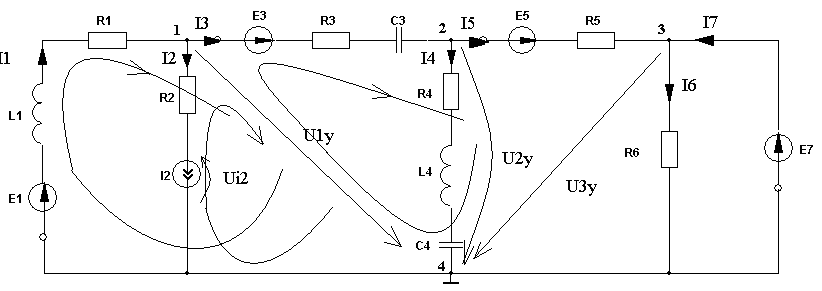
Будем считать, что все источники - гармонического воздействия с одной и той же частотой. Применим метод в комплексной форме.

N_уз.=4 N_E=1 (Е7)

N_ур.=4-1-1=2

Выбираем 4 как базисный узел, I₂=J₂ . Указываем узловые напряжения, направляя их к базисному узлу, при этом

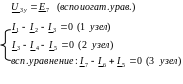Выразим токи ветвей через узловые напряжения с использованием законов Ома и Кирхгофа. Используем для этого вспомогательные контуры. Они показаны на схеме и обязательно проходят через базисный узел (4).

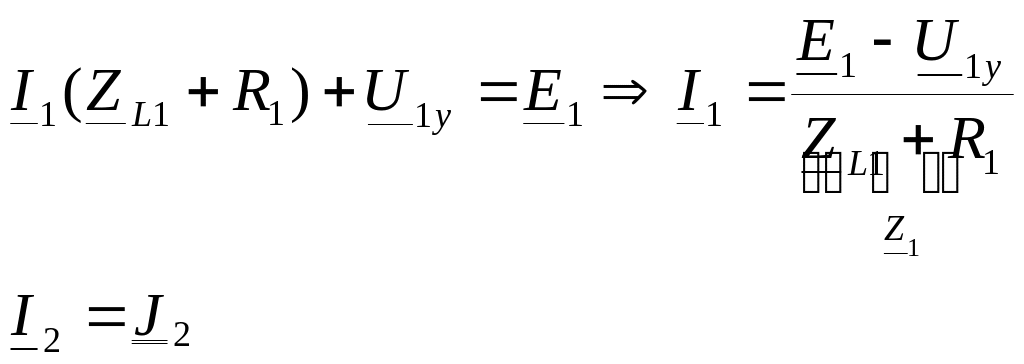
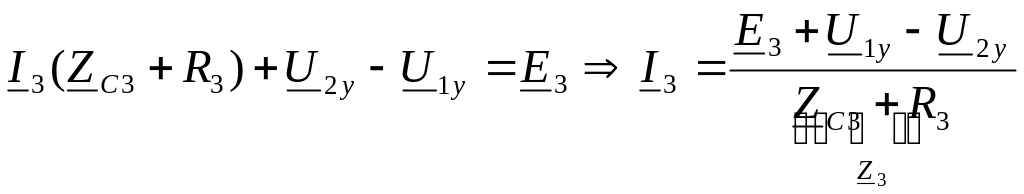
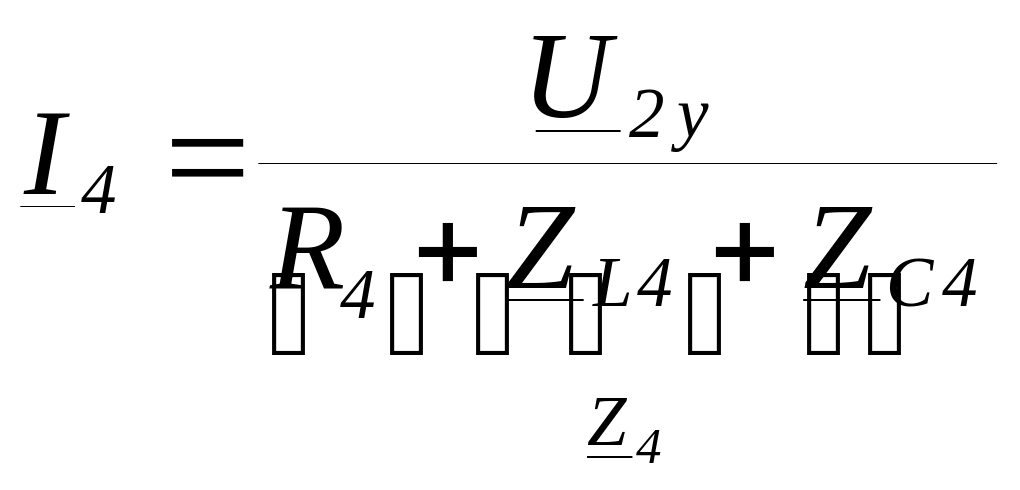
В систему уравнений подставляются формулы токов и делаются алгебраические преобразования, цель которых привести систему к стандартному виду.

Стандартный вид:

Решив эту систему относительно узловых напряжений, подставляем полученные значения в формулы нахождения токов ветвей через узловые напряжения. Можно сделать смену знаков в уравнениях.