1.Предмет и задачи космической геодезии.Космическая геодезия – это раздел геодезической науки, в котором научные и научно технические задачи геодезии решаются на основе наблюдений за естественными и искусственными спутниками Земли.При этом основная задача состоит в изучении формы, размеров и гравитационного поля Земли.Предметом изучения космической геодезии является Земля. При этом следует отметить, что методы космической геодезии хорошо подходят для геодезического изучения других небесных тел (Луна, Марс и прочие).Космическая геодезия использует наблюдения, которые проводят в околоземном пространстве. Под околоземным пространством обычно понимают всё пространство от верхних границ воздухоплавания и до лунной орбиты.

2.

X, Y, Z – геоцентрическая с.к., т.е. т. О – центр масс Земли;т. Р – пункт наблюдения на земной поверхности;т. S – спутник; - геоцентрический радиус-вектор пункта наблюдения; - геоцентрический радиус-вектор спутника; - топоцентрический радиус-вектор спутника.Из рисунка видно: - основное уравнение космической геодезии.

3.Классификация задач в космической геодезии.Задачи космической геодезии обычно классифицируют по характеру и по виду определённых величин.Классификация задач в космической геодезии по их характеру: динамические; геометрические;смешанные.Динамическими называют такие задачи, которые решаются с использованием теории движения небесных тел.Смешанными называются такие задачи, которые решаются как с использованием геометрических построений, так и теории движения небесных тел.Геометрические задачи решаются без использования теории движения на основе геометрических построений.Классификация задач в космической геодезии по виду определяемых величин:прямые;обратные.

4.Классификация координатных систем.В космической геодезии рассматривается большое количество самых разнообразных задач и поэтому в ней используются практически все известные с.к. из высшей геодезии, астрономии, небесной механики и других дисциплин.Любые системы координат могут быть:инерциальные;неинерциальные.В космической геодезии инерциальные с.к. – это такие системы, которые связаны со звёздами.Классификация координатных систем производится по трём признакам:вид координатной системы;расположение начала отсчёта;ориентация основной и начальной плоскостей.По виду координатные системы делятся на:прямоугольная декартовая с.к. (математическая – X, Y, Z);сферическая с.к.;эллиптическая с.к. (геодезическая – B, L, H);тороидальная с.к.;цилиндрическая с.к. и др.По расположению начала отсчёта координатные системы бывают:геоцентрические, т.е. начало координат находится в центре масс Земли;референцные, т.е. начало координат находится в центре референц-эллипсоида;топоцентрические, т.е. начало координат находится в некоторой точке на поверхности Земли;спутникоцентрические, т.е. начало координат находится в центре масс спутника;барицентрические, т.е. начало координат находится в центре масс системы тел.По ориентации основной и начальной плоскостей:А) классификация координатных систем по расположению основной плоскости:1. экваториальная с.к. – основная плоскость лежит в плоскости экватора или ей параллельна.2. горизонтальная с.к. – основная плоскость лежит в плоскости горизонта или параллельна ему.3. орбитальная с.к. – основная плоскость лежит в плоскости орбиты какого-либо небесного тела.Б) классификация координатных систем по расположению начальной плоскости:1. гринвичская с.к. – начальная плоскость лежит в гринвичском меридиане.2. звёздная с.к. – начальная плоскость находится в плоскости равноденственных точек (весеннего и осеннего равноденствия).

5.Инерциальная звёздная система координат.ИСЗ движется по орбите вокруг центра масс Земли, но не участвует в её суточном вращении. Поэтому положение спутника в пространстве удобно определять в такой с.к., которая не вращалась бы вместе с Землёй. Для этого в космической геодезии используется инерциальная звёздная с.к. У этой системы начало координат находится в центре масс Земли, т.е. эта система является геоцентрической. Начальная плоскость системы совпадает с меридианом равноденственных точек. Основная плоскость совпадает с плоскостью небесного экватора некоторой начальной эпохи. Ось Z системы направлена на северный полюс мира той же начальной эпохи.γ₀ – точка весеннего равноденствия на некоторую начальную эпоху;Р₀ – северный полюс мира на некоторую начальную эпоху;x₀, y₀, z₀ – прямоугольные координаты;r₀, α₀, γ₀ – сферические координаты.Положение спутника в такой системе определяется либо прямоугольными координатами, либо сферическими:r₀ – радиус-вектор;α₀ – прямое восхождение – угол поворота текущего меридиана относительно начальной плоскости;δ₀ – склонение – угол возвышения радиус-вектора над плоскостью экватора.Рассмотренная звездная система координат в астрономии называется 2ой экваториальной системой.

Данная с.к. закреплена координатами небесных светил. Координаты этих объектов можно найти в астрономических ежегодниках.

6.В АЕ координаты звёзд даны на некоторую эпоху каталога Т₀. Как известно стечением времени координаты звёзд непрерывно меняются вследствие процессов прецессии и нутации.Прецессия – колебания оси вращения Земли.Нутация – дрожание оси вращения Земли.Возникает задача преобразования координат от эпохи каталога на текущую дату. Такая задача решается в два приёма. На первом этапе координаты исправляются за влияние прецессии. А на втором этапе – за влияние нутации.Исправление координат за влияние прецессии производится с помощью прецессионных параметров Ньюкома.Проведём меридиан через Р₀ и Р₁, этот меридиан пересечёт исходное положение небесного экватора в точке А₀, а текущее положение – в точке А₁.Θ – угол разворота оси Z;ξ₀ – угол между А₀ и γ₀ прецессионные параметры Ньюкома.ξ – угол между А₁ и γ₁Данные параметры показывают каким образом развернулась система координат относительно исходного положения

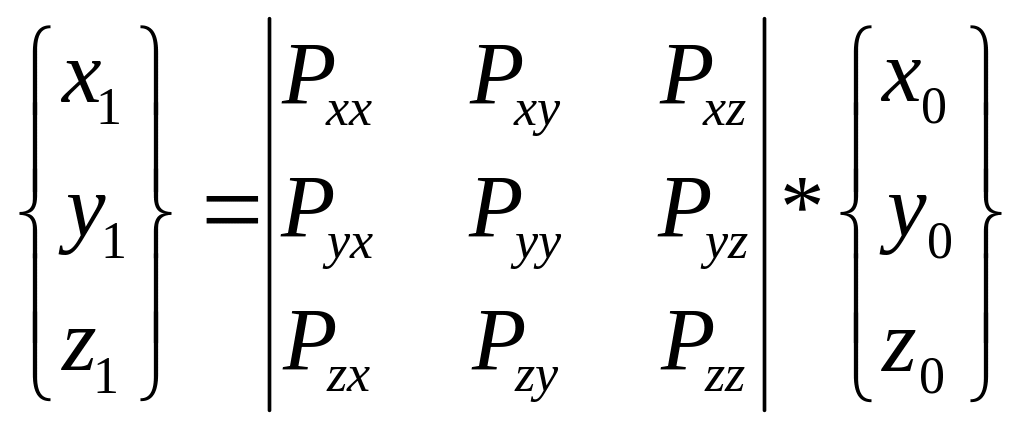
где Р_{i j} = f (θ; ξ₀; ξ);x₀, y₀, z₀ – координаты на эпоху каталога;x₁, y₁, z₁ – координаты исправленные за влияние прецессии (средние координаты);Р_{i j} – коэффициенты перехода, которые являются функцией от параметров Ньюкома.Порядок вычисления коэффициентов перехода излагается в АЕ.На следующем этапе средние координаты исправляются за влияние нутации:

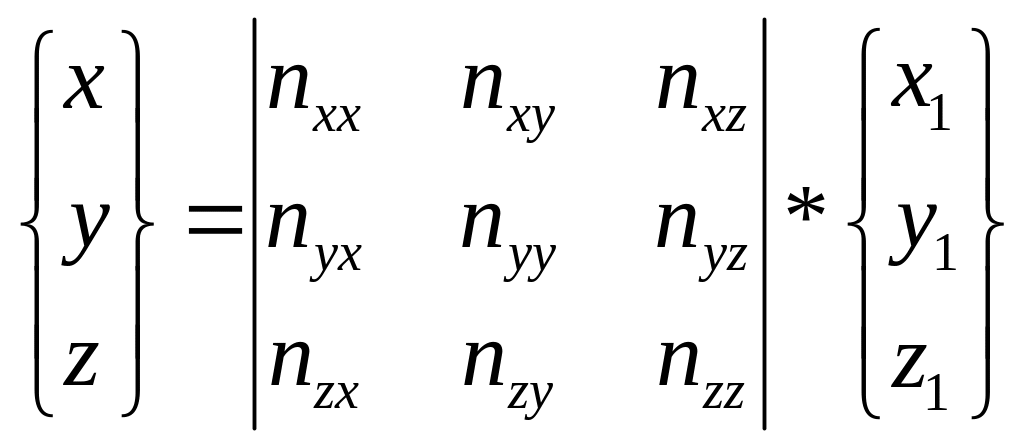
x, y, z – координаты исправленные за влияние прецессии и нутации.n_{i j} – коэффициенты перехода, которые вычисляются согласно АЕ.После исправления координат за прецессию и нутацию они ещё проводятся к видимым местам. Кроме того положение светил исправляется за собственное движение звёзд. Порядок этих вычислений дан в АЕ-ах.

7.Гринвичская система координат.В этой с.к. начало координат находится в центре масс Земли, т.е. эта система является геоцентрической. Начальная плоскость системы совмещена с гринвичским меридианом. Основная плоскость находится в плоскости небесного экватора. Ось Z системы направлена на северный полюс. Т.о. эта с.к. неинерциальная, т.к. она вращается вместе с Землёй.

В качестве точки северного полюса принимается его среднее положение. Оно соответствует местоположению северного полюса в 1905 году. Это положение принято Международной службой движения полюсов.x_г, y_г, z_г – прямоугольные гринвичские координаты спутника;r, t, δ – сферические координаты спутника;r – радиус-вектор;t – часовой угол, который считается по часовой стрелке;δ – склонение – угол возвышения радиус-вектора над плоскостью экватора;S – Гринвичское звёздное время.t = S – α – основная формула звёздного времени.α₀ – прямое восхождение – угол поворота текущего меридиана относительно начальной плоскости.

8.9.Преобразование координат и компонентов скорости из звёздной системы в гринвичскую.

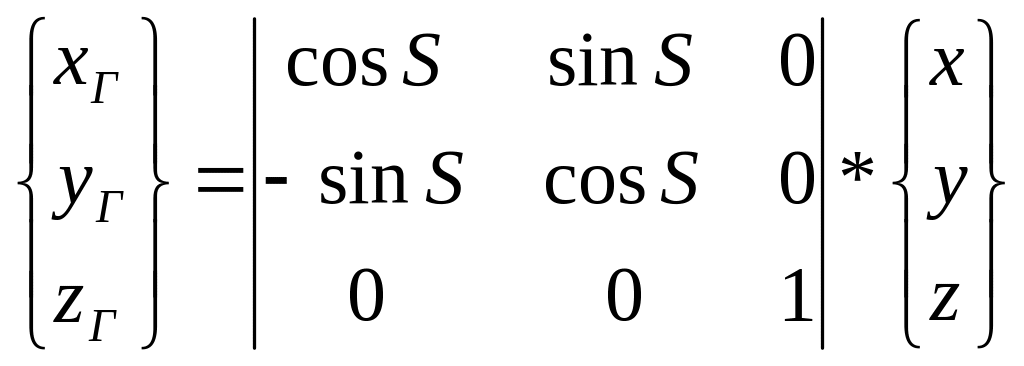
S = ω*T.ω – угловая скорость вращения Земли;T – время.

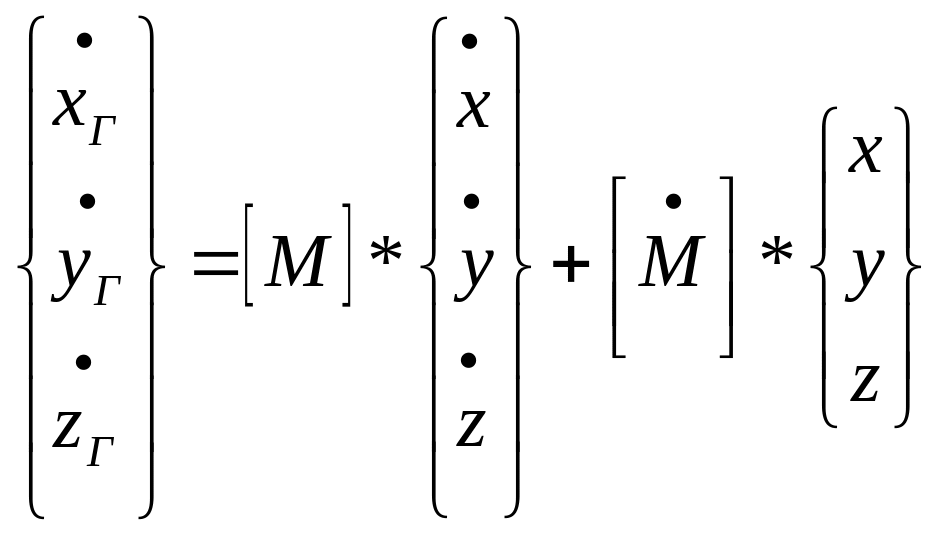
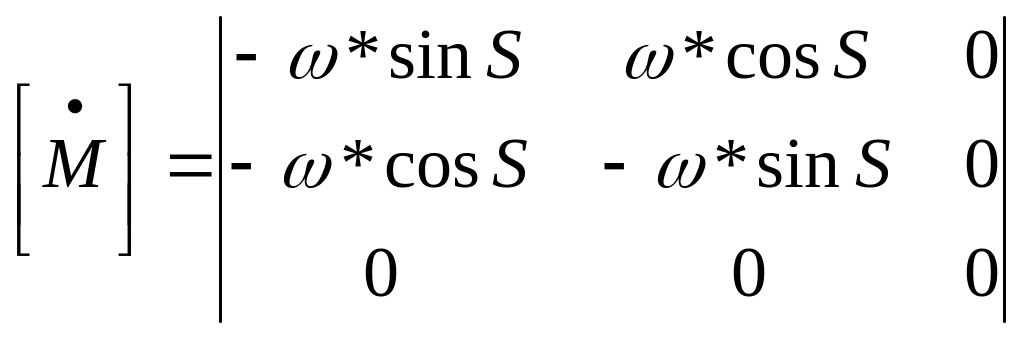
10.Топоцентрические системы координат.В топоцентрических системах координат начало координат всегда располагается в некоторой точке на поверхности Земли. Дальше название системы будет зависеть от того как ориентированы её координатные оси. Если оси топоцентрической системы будут параллельны осям звёздной с.к., то мы получим топоцентрическую звёздную с.к. Если же оси будут параллельны осям гринвичской с.к., то мы получим топоцентрическую гринвичскую с.к.

Для примера изобразим геоцентрическую звёздную и топоцентрическую звёздную с.к..геоцентрическая звёздная с.к.:r, α, δ.топоцентрическая звёздная с.к.:ρ, α’, δ’.α’- топоцентрическое прямое восхождение;δ’ – топоцентрическое склонение.R – радиус-вектор пункта наблюдения.

11.Топоцентрическая горизонтальная система координат.Эта система связана с направлением нормали к поверхности эллипсоида. Основная плоскость системы находится в плоскости горизонта. Ось x направлена по касательной к меридиану в направлении северного полюса, а ось y направлена вверх по направлению нормали.Координаты пункта наблюдения обычно задаются в геодезической с.к.: B, L, H. Координаты пункта наблюдения можно преобразовать в геодезическую прямоугольную с.к.(см форм.4)

N – радиус кривизны первого вертикала;a – большая полуось;e – эксцентриситет земного эллипсоида.Иногда необходимо делать обратный переход, т.е. координаты пункта наблюдения даны в прямоугольной геоцентрической с.к., а необходимо найти геодезические координаты (B, L, H).Такое преобразование в конечном виде сделать нельзя, поэтому используют либо приближённые формулы, либо итерационные методы.Так же бывает необходимо координаты спутника преобразовать из геоцентрической гринвичской с.к. в горизонтную(см форм.3)

13.Кеплеровы элементы орбиты спутника и орбитальная система координат.

Будем рассматривать орбитальную систему связанную с плоскостью орбиты спутника. Использовать будем плоскую полярную или декартовую с.к.Рассмотрим эллиптическую орбиту спутника:F – фокус;е – эксцентриситет;а – большая полуось. При движении спутника по эллиптической орбите точка притяжения (ц.м. Земли), находится в одном из фокусов эллипса.Точка орбиты, которая дальше всех расположена от центра масс Земли, называется апогей орбиты А.Точка орбиты, которая ближе всех расположена к центру масс Земли, называется перегей орбиты П.Большая полуось = линия АБСИД.В орбитальной с.к. начало координат располагается в фокусе, т.е. в центре масс Земли. Ось X располагают по линии абсид в сторону перегея, а ось Y – перпендикулярно оси X. Ось Z направлена перпендикулярно плоскости орбиты.υ – истинная аномалия.Р – фокальный параметр, характеризует расстояние от фокуса до орбиты спутникаР = а(1 - е²)

Достроим эллипс до окружности, продолжим радиус-вектор до этой окружности и проведём радиус-вектор получившейся точки.Е – эксцентрическая аномалия, характеризует угол поворота псевдо точки вне центра.(см форм 6)Орбитальная с.к. даёт возможность определить положение спутника на орбите для любого момента времени.

14.Кроме этого необходимо знать расположение орбиты в пространстве. Для этого надо знать Кеплеровы элементы орбиты.N – восходящий узел;N’ – низходящий узел;NN’ – линия узлов.Ω – долгота восходящего узла;ω – долгота (аргумент) перегея;ι – наклон орбиты.Данные три элемента дают расположение орбиты в пространстве.а, е, Ω, ω, ι – Кеплеровы элементы

1. а, е – характеризуют форму и размеры орбиты;

2. Ω, ω, ι – характеризуют положение орбиты в пространстве;

τ – динамический элемент, характеризует движение спутника – некоторый начальный момент времени в который спутник находится в перегее.

12.Системы измерения времени в космической геодезии.В космической геодезии используются системы:

всемирного времени UT;эффемеридного времени ЕТ;атомного времени АТ;всемирного координированного времени UTC.Всемирное время UT.Среднее солнечное время на Гринвичском меридиане.Оно имеет несколько разновидностей:

1. UT0 – время, которое получено непосредственно из наблюдений – угол между мгновенным положением Гринвичского меридиана и кругом склонения среднего Солнца.

Непосредственно из наблюдений определяют звёздное время, а солнечное время вычисляют по формулам перехода:

UT0 = (S - S₀) + ν*(S – S₀)

S – звёздное время полученное из наблюдений;

S₀ – звёздное время в предшествующую гринвичскую полночь;

ν – коэффициент перехода.

Время UT0 является неравномерным из-за движения земного полюса и непостоянства скорости вращения Земли. Для того чтобы рассчитывать положение спутника на орбите необходимо строго равномерное время, поэтому вводятся дополнительные шкалы всемирного времени.

2. UT1 – это время UT0 с поправкой за движение земных полюсов.

3. UT2 – это время UT0 с поправкой за сезонную неравномерность скорости вращения Земли.

Систему времени UT2 можно считать равномерной в течении больших промежутков времени (до нескольких лет). В этой связи было решено ввести строго равномерную систему времени – эффемеридное время ЕТ.ЕТ основано на наблюдениях за движением Луны. Из наблюдений за движением Луны определяется поправка к всемирному времени ΔТ (публикуется в АЕ).ЕТ = UT2 + ΔТ.Недостатком эффемеридного времени является то, что поправка ΔТ точно известна только на текущий момент времени. Для последующих промежутков времени эта поправка определяется экстраполяцией.Атомное время АТ.Атомная шкала времени основана на высокостабильных атомных эталонах частоты.Единицей атомного времени является 1 атомная секунда. Точность атомной секунды соответствует 12-ому знаку после запятой. В настоящее время атомная шкала времени является основной.Всемирное координированное время UTC. В системе UTC передаются сигналы точного времени. Система UTC отличается от АТ не более чем на 1 секунду. Всемирное координированное время – это ступенчато равномерное время.

16.Теория движения выводится на основе закона всемирного тяготения и второго закона Ньютона.Введём направляющие косинусы радиус – вектора:

α_x = cos α

α_y = cos β

α_z = cos γ

Эти направляющие косинусы есть соответствующие координаты радиус-вектора .

α_x = cos α = x/r

α_y = cos β = y/r

α_z = cos γ = z/r

- закон всемирного тяготения

«-» – соответствует притяжению.

, - ускорение спутника.

f *M = μ – гравитационный параметр

Спроектируем на координатные оси:

Система (1) – это система трёх нелинейных дифференциальных уравнений второго порядка. Она описывает движение спутника в пространстве.