3.2. Определение aо

Выше была введена величина a_о (3.4), полученная при рассмотрении потенциала обтекания эллипсоида безграничным потоком, который на поверхности эллипсоида имеет вид:

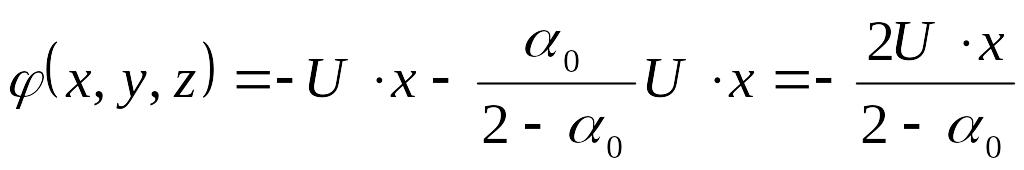(3.5)

Именно это свойство эллипсоида позволяет существенно упростить функцию Кочина и получить выражение для коэффициента волнового сопротивления в довольно простом виде:

(3.6)

Определение a_о для эллипсоида вращенияс осью, направленной вдоль оси Ох

В этом случае b=c=r. Введем новые обозначения:

, , , . (3.7)

При ε₁<1 - получаем "сплюснутый" эллипсоид. Формула для определения a_о при ε₁<1 будет иметь следующий вид:

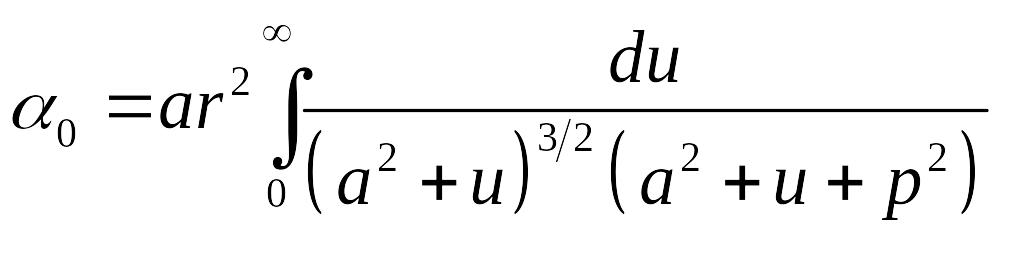(3.8)

Вводя подстановку , после ряда несложных преобразований получим:

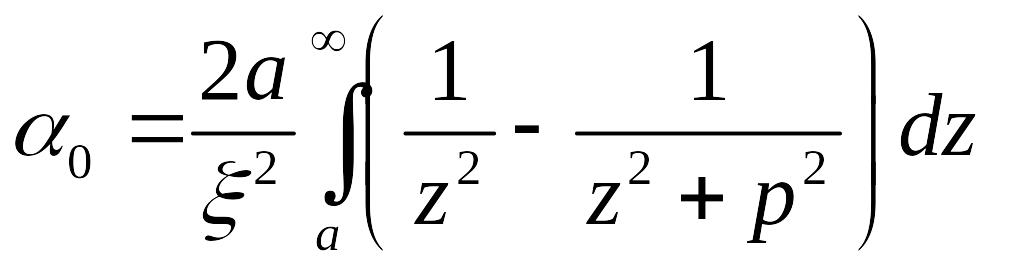(3.9)

В итоге, с учетом сделанных обозначений (3.9), получим для эллипсоида с осью вращения, направленной вдоль оси Ох:

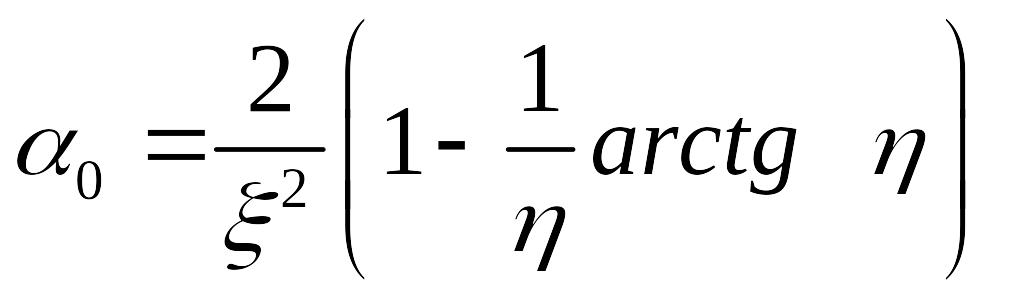(3.10)

Исследование полученного выражения показывает, что . Вид функции a_о(e₁) показан на рис. 2.

Рассмотрим свойства полученного выражения:

При приближении к сфере, то есть e₁®0 , h®0, x®0, формула даёт значения

стремящиеся к (случай aо для сферы), но применять её при e=1 нельзя.

Рассмотрим разложение в ряд Маклорена функции (3.10) вблизи точки, где e₁®1,

x=h ®0. Ограничиваясь двумя членами в разложении, имеем:

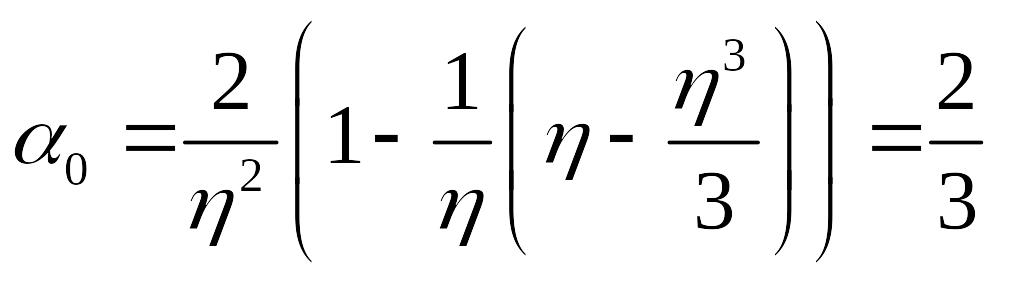
Таким образом, aо можно рассматривать как непрерывную функцию

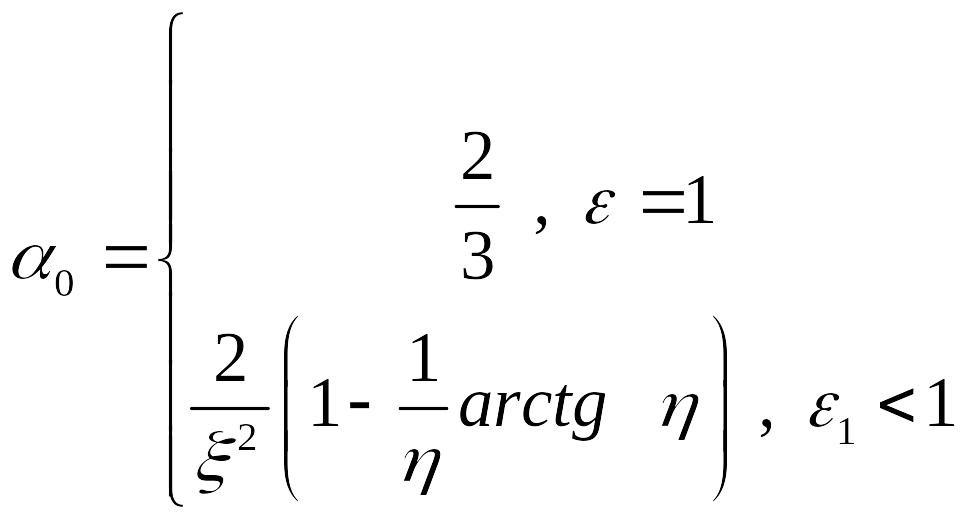(3.11)

При e₁ ®¥, h®1, x ®e₁ aо, как видно из (3.10), стремится к нулю, то есть при

e₁ ® ¥, aо ® 0 ("нить", расположенная параллельно потоку).

При e ®0, x ®1, , a_о→2, то есть при e₁®0, a_о®2

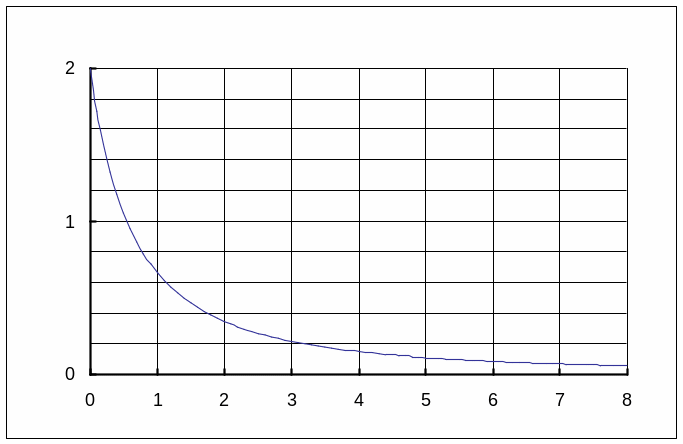
Рис. 2 a_о(e₁) для эллипсоида с осью вращения, направленной вдоль оси Ox

3.3. Вычисление функции Бесселя.

Как видно из формулы (3,1), в ходе вычисления коэффициента волнового сопротивления требуется вычисление функции Бесселя (I_3/2(z)), а точнее ее квадрата.

Как известно:

(3.12)

Введем функцию:

(3.13)

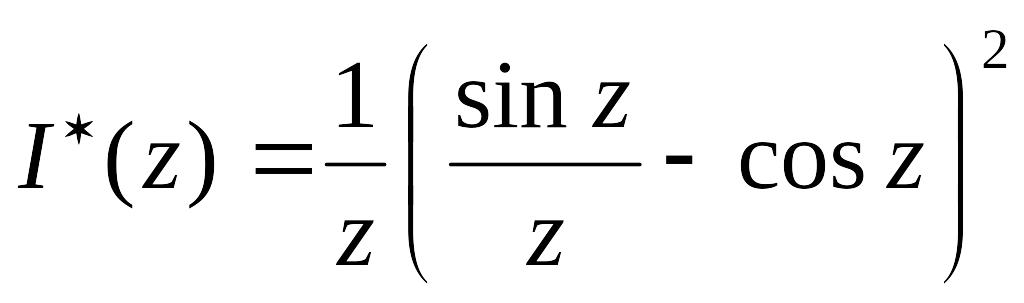(3.14)

График функции I^*(z) приведен на рис.4. Свойства этой функции аналогичны свойствам функции I_3/2(z). Так при z®¥ функция I^*(z)®0 и функция I_3/2(z)®0. При z®0 функция I^*(z)®0.

Рассмотрим асимптотическое поведение I^*(z) при z®0. Ограничимся двумя членами при разложении в ряд Маклорена.

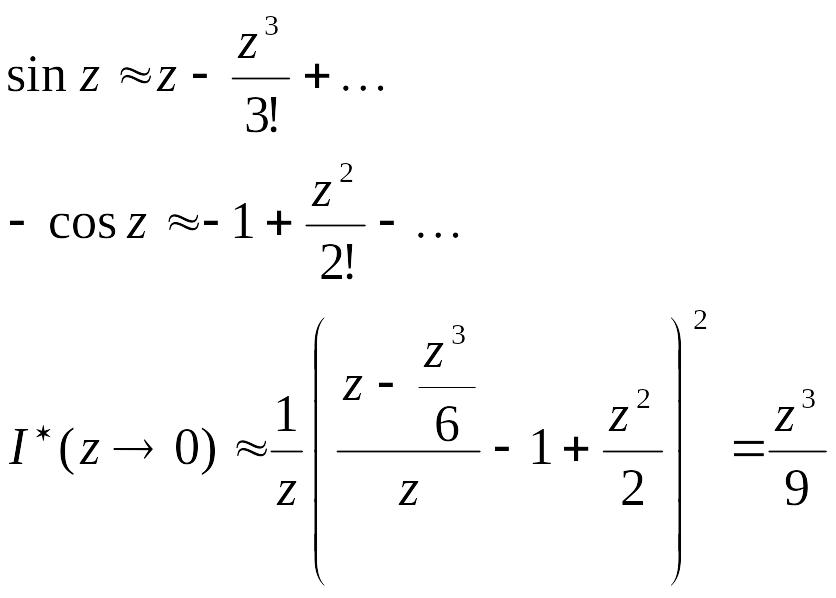
Таким образом I^*(z) вблизи точки z = 0 эквивалентна , то есть:

(3.15)

С учетом (3.13) сила волнового сопротивления запишется так:

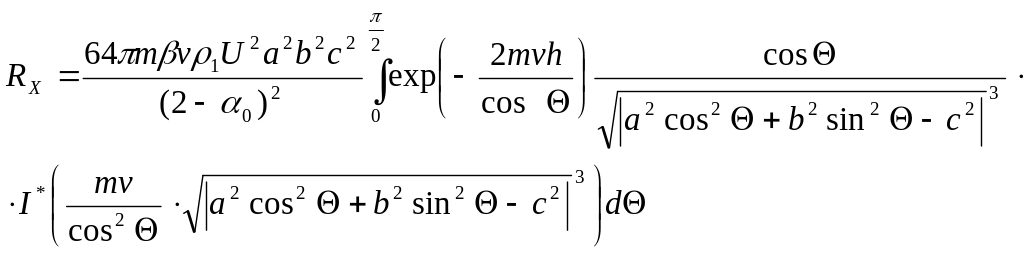(3.16)

I^*(z)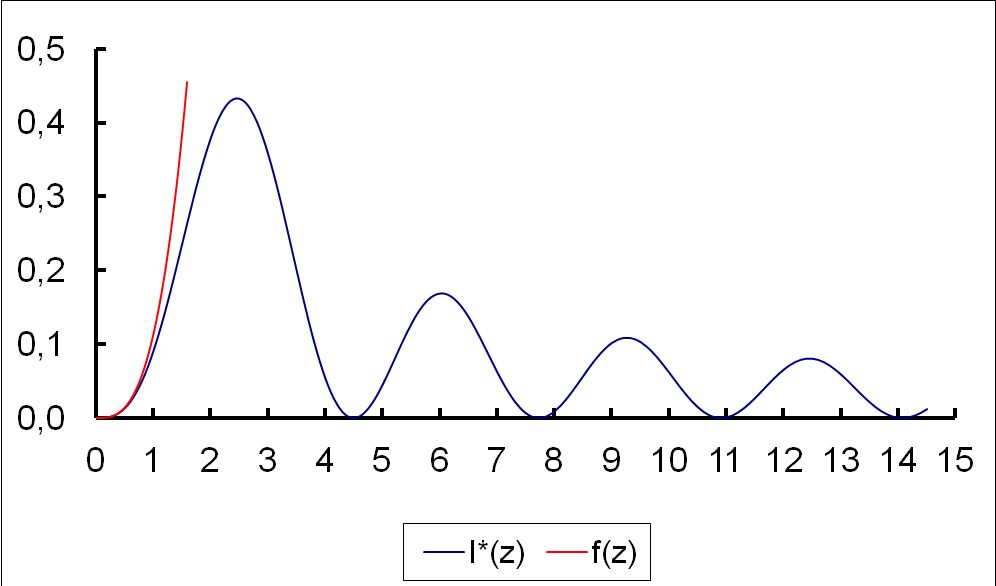

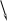
Рис. 4