Глава 3. Постановка задачи, определение сил, действующих на тело.
Рассмотрим линейную пространственную задачу о волновых движениях, возникающих вблизи свободной поверхности, при равномерном, прямолинейном, горизонтальном перемещении твердого тела в жидкости.
Н.Е. Кочиным предложено общее решение такой задачи для тела произвольной формы, движущегося под свободной поверхностью. В данной работе приведено решение и расчет для тела простейшей формы – эллипсоида.
Волны. Образующиеся на свободной поверхности при движении тела на постоянной глубине h с постоянной скоростью U, будем считать малыми, а поверхность тела достаточно гладкой.
Задачу будем решать в подвижной системе координат. Волновые движения можно рассматривать в невязкой жидкости, а само движение – безвихревым, При движении тела,в жидкости ограниченной свободной поверхностью, на последней будут возникать волны (корабельные, вынужденные). Поскольку течение безвихревое, то скорости жидких частиц в волновом движении:
где
- потенциал вызванных скоростей волнового
движения, возникающего при движении
тела с постоянной скоростью
,
свободных волн на поверхности перед
телом нет (движение на тихой воде).
Следовательно задача сводится к отысканию
потенциала. Однако следует помнить что
цель задачи это не определение φ, а
определение силы волнового сопротивления.
Это связано с распределением давления,
что в свою очередь связано с распределением
скоростей.
Если
обозначить
– значение в неподвижной системе:
,
φ – в подвижной:
.
Тогда в подвижной с.к. производные потенциала не будут зависеть от времени
Запишем
граничные условия в подвижной с.к.
x,y,z → Ω
Ω – весь объем нижнего полупространства, за вычетом объема, ограниченного S.
На свободной поверхности (в неподвижной системе), при z = 0
или
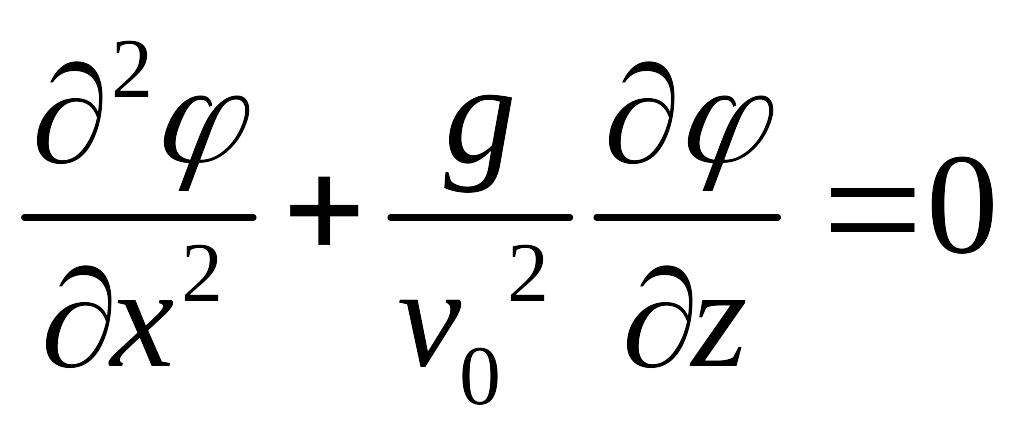
-объединенное динамическое и кинематическое граничное условие.
На поверхности тела условие непротекания.
Условие
на ∞:
M
= const. при
При z→∞, φ→0
Условие отсутствия свободных волн далеко перед телом:
φ→0 при x→∞
Рис. 1 к постановке задачи:
h
U
3.1. Вычисление волнового сопротивления
Проекция суммарной гидродинамической силы на направление движения тела, совпадающего с горизонтальной осью Ох, - Rx, названная силой волнового сопротивления. Кочиным Н.Е. была предложена формула для силы волнового сопротивления, которая справедлива для тела, движущегося под свободной поверхностью [3]:
,
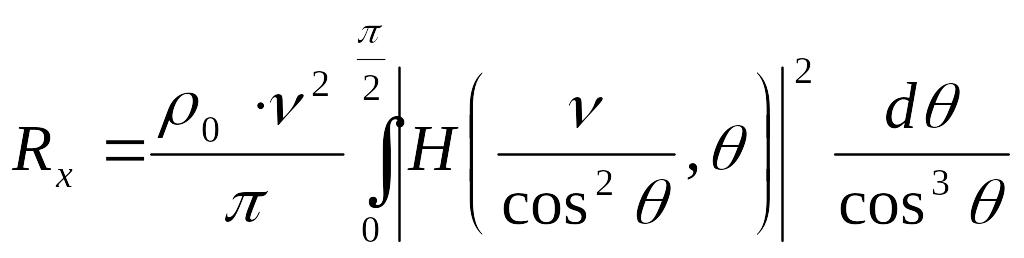(3.1)
где
rо – плотность
жидкости,
-
функция Кочина,
,
(3.2)
g = 9,81 м/с2 – ускорение свободного падения, U – скорость движения тела.
Существенно упростить вычисление функции Кочина можно, если представить потенциал относительного движения в виде:
,
где f(q) – функция координат, принимающих на поверхности тела постоянное значение. В случае эллипсоида Rx может быть вычислено по формуле:
,
(3.3)
где a, b, c –полуоси эллипсоида в направлении x, y, z соответственно, причем:
,
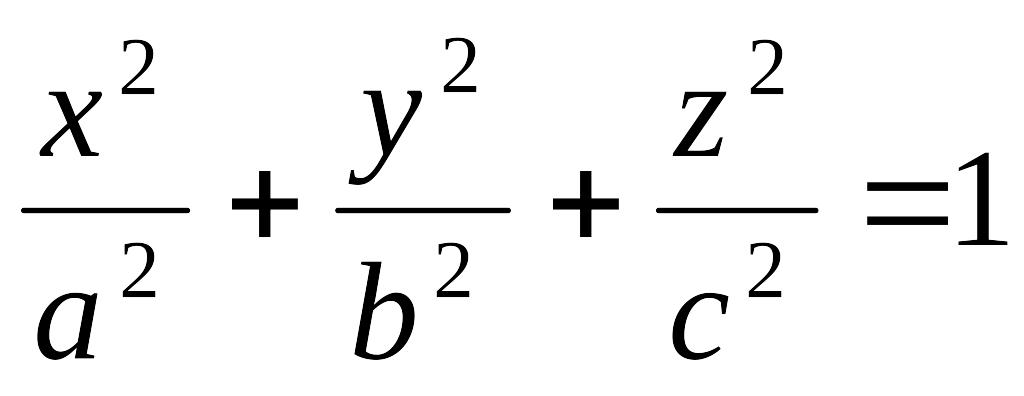I3/2(z) – функция Бесселя, aо – величина, определяемая интегралом:
,
(3.4)
где u – координата, в выбранной системе координат.
Свойства aо будут рассмотрены ниже.
Полученные формулы позволяют получить Rx эллипсоида при допущениях линейной теории.
В дальнейшем будет рассматриваться случай движения под свободной поверхностью.