44

Лекции Программируемые логические матрицы

PLM

Астраханцев Александр Владимирович

доработано - Ажимов Василий Васильевич

1. Программируемые логические матрицы, программируемая матричная логика, базовые матричные кристаллы

§ 1.1. Вводные замечания

В цифровые системы обработки информации входят процессор, память, периферийные устройства и интерфейсные схемы. Процессор является стандартным устройством - он не изготовляется для конкретной системы по специальному заказу, а решает требуемую задачу путем последовательного выполнения определенных команд из присущей ему системы команд.

Память также реализуется стандартными микросхемами — ее функции остаются одними и теми же для разных систем.

Стандартные БИС/СБИС лидируют по уровню интеграции, т.к. высокая стоимость проектирования оптимизированных по плотности БИС/СБИС, достигающая сотен миллионов долларов, оказывается в данном случае приемлемой, поскольку раскладывается на большое число производимых микросхем.

Наряду со стандартными, в системе присутствуют и некоторые нестандартные части, специфичные для данной разработки. Это относится к схемам управления блоками, обеспечения их взаимодействия и др. Реализация нестандартной части системы исторически была связана с применением микросхем малого и среднего уровней интеграции. Применение МИС и СИС сопровождается резким ростом числа корпусов ИС, усложнением монтажа, снижением надежности системы и ее быстродействия. В то же время заказать для системы специализированные ИС высокого уровня интеграции затруднительно, т. к. это связано с очень большими затратами средств и времени на проектирование БИС/СБИС.

Возникшее противоречие нашло разрешение на путях разработки БИС/СБИС с программируемой и репрограммируемой структурой.

Первыми представителями указанного направления явились программируемые логические матрицы ПЛМ (PLA, Programmable Logic Array), программируемая матричная логика ПМЛ (PAL, Programmable Array Logic) и базовые матричные кристаллы БМК, называемые также вентильными матрицами ВМ (GA, Gate Array), PLA и PAL в английской терминологии объединяются также термином PLD, Programmable Logic Devices.

Развитие БИС/СБИС с программируемой и репрограммируемой структурой оказалось настолько перспективным направлением, что привело к созданию новых эффективных средств разработки цифровых систем, таких как CPLD (Complex PLD), FPGA (Field Programmable GA) и SPGA (System-in Programmable GA).

В рамках современных БИС/СБИС с программируемой и репрограммируемой структурой стала решаться и задача создания целой системы на одном кристалле.

§ 1.2. Программируемые логические матрицы и программируемая матричная логика (плм и пмл)

Программируемые логические матрицы

Программируемые логические матрицы появились в середине 70-х годов Основой их служит последовательность программируемых матриц элементов И и ИЛИ. В структуру входят также блоки входных и выходных буферных каскадов (БВх и БВых).

Входные буферы, если не выполняют более сложных действий, преобразуют однофазные входные сигналы в парафазные и формируют сигналы необходимой мощности для питания матрицы элементов И.

Выходные буферы обеспечивают необходимую нагрузочную способность выходов, разрешают или запрещают выход ПЛМ на внешние шины с по­мощью сигнала ОЕ, а иногда выполняют и более сложные действия.

Основными параметрами ПЛМ (рис 1) являются число входов т, число термов l и число выходов п.

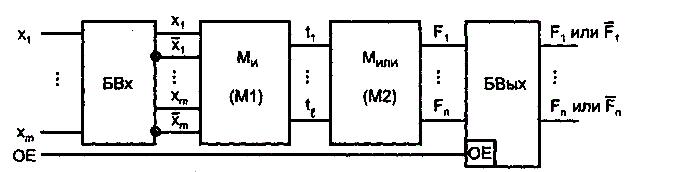
Рис.1.1. Базовая структура ПЛМ

ременные X1..Xm подаются через БВх на входы элементов И (конъюнкторов), и в матрице И образуются l термов. Под термом здесь понимается конъюнкция, связывающая входные переменные, представлен­ные в прямой или инверсной форме. Число формируемых термов равно числу конъюнкторов или, что то же самое, числу выходов матрицы И.

Термы подаются далее на входы матрицы ИЛИ, т. е. на входы дизъюнкторов, формирующих выходные функции. Число дизъюнкторов равно числу вырабатываемых функций п.

Таким образом, ПЛМ реализует дизъюнктивную нормальную форму (ДНФ) воспроизводимых функций (двухуровневую логику). ПЛМ способна реализовать систему n логических функций от т аргументов, содержащую не более l термов. Воспроизводимые функции являются комбинациями из любого числа термов, формируемых матрицей И. Какие именно термы будут выработаны и какие комбинации этих термов составят выходные функции, определяется программированием ПЛМ.

Схемотехника ПЛМ

Выпускаются ПЛМ как на основе биполярной технологии, так и на МОП-транзисторах. В матрицах имеются системы горизонтальных и вертикальных связей, в узлах пересечения которых при программировании создаются или ликвидируются элементы связи.

На рис. 1.2, а в упрощенном виде (без буферных элементов) показана схемотехника биполярной ПЛМ К556РТ1 с программированием пережиганием перемычек. Показан фрагмент для воспроизведения системы функций

F1 = x1^x2x3Vx2x3^Vx1x4^ = t1Vt2Vt3

F2 =x1^x2^x3Vx1x2^x3^Vx1x2x4Vx2x3^x4 = t1Vt4Vt5Vt6

F3 = x1x4^Vx1x2^ = t1V t7

размерностью 4, 7, 3. Параметрами микросхемы К556РТ1 являются 16, 48, 8. Элементами связей в матрице И служат диоды, соединяющие горизонтальные и вертикальные шины, как показано на рис. 1.2, б, изображающем цепи выработки терма t1. Совместно с резистором и источником питания цепи выработки термов образуют обычные диодные схемы И. До программирования все перемычки целы, и диоды связи размещены во всех узлах координатной сетки. При любой комбинации аргументов на выходе будет ноль, т. к. на вход схемы подаются одновременно прямые и инверсные значения аргументов, а хх^ = 0. При программировании в схеме оставляются только необходимые элементы связи, а ненужные устраняются пережиганием пе­ремычек. В данном случае на вход конъюнктора поданы x1,x2 и x3. Высокий уровень выходного напряжения (логическая единица) появится только при наличии высоких напряжений на всех входах, низкое напряжение хотя б на одном входе фиксирует выходное напряжение на низком уровне, т. к открывается диод этого входа. Так выполняется операция И, в данном случае вырабатывается терм x1x2x3.

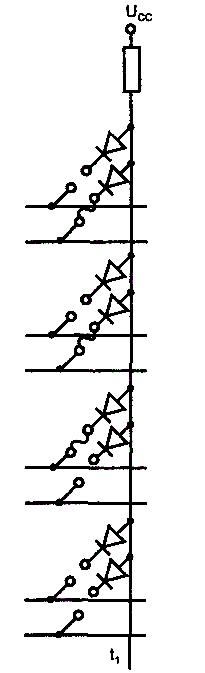б а

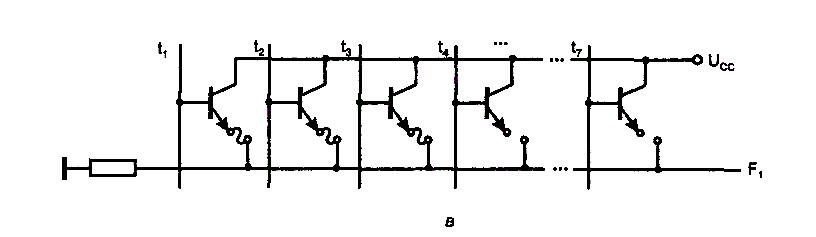
Рис. 1.2. Схемотехника ПЛМ, реализованной в биполярной технологии (а), и элементы связей в матрицах И (б) и ИЛИ (в)

Элементами связи в матрице ИЛИ служат транзисторы (рис. 1.2, в), включенные по схеме эмиттерного повторителя относительно линий термов и образующие схему ИЛИ относительно выхода (горизонтальной линии). На рис. 1.2, в показана выработка функции F1 Работа схемы ИЛИ, реализованной в виде параллельного соединения эмиттерных повторителей, рассмотрена ранее в § 1.2.

При изображении запрограммированных матриц наличие элементов связей целые перемычки) отмечается точкой в соответствующем узле.

В схемах на МОП-транзисторах в качестве базовой логической ячейки используют инвертирующие (ИЛИ-НЕ, И-НЕ). Соответственно этому меняются и операции, реализуемые в первой и второй матрицах ПЛМ. В частности, в схемотехнике п-МОП базовой ячейкой обычно служит ячейка ИЛИ-НЕ, а структура ПЛМ имеет вид (рис. 1.3). Такая ПЛМ является последовательностью двух матриц ИЛИ-НЕ, одна из которых служит для выработки термов, другая — для выработки выходных функций.

Терм t1 в данном случае равен: , а функция

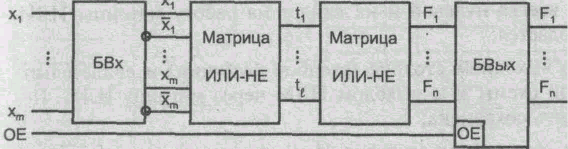
Рис. 1.3. Схемотехника ПЛМ, реализованной на МОП-транзисторах

На основании этих выражений можно заключить, что известная связь между операциями, выражаемая правилами де Моргана, говорит о фактическом совпадении функциональных характеристик биполярной ПЛМ и ПЛМ на МОП-транзисторах: если на входы последней подавать аргументы, инвертированные относительно аргументов биполярной ПЛМ, то на выходе получим результат, отличающийся от выхода биполярной ПЛМ только инверсией.

Подготовка задачи к решению с помощью ПЛМ

Имея в виду подбор ПЛМ минимальной сложности, следует уменьшить по возможности число термов в данной системе функций. Содержанием минимизации функций будет поиск кратчайших дизъюнктивных форм. Вести поиск минимальных по числу термов представлений задачи следует до уровня, когда число термов становится равным l — параметру имеющихся ПЛМ. Дальнейшая минимизация не требуется. Если размерность имеющихся ПЛМ обеспечивает решение задачи в ее исходной форме, то минимизация не требуется вообще, т. к. не ведет к сокращению оборудования.

Программирование ПЛМ

Программирование ПЛМ, выполняемое пользователем, проводится с помощью специальных устройств (программаторов) и сведения для них с данной ПЛМ должны иметь определенную форму. Имеются программаторы, которые принимают в качестве информации о ПЛМ таблицу функционирования (истинности), однако удобнее задавать сведения о самих перемычках. Символы, используемые при таком задании сведений для программирования ПЛМ:

-Н— переменная входит в терм в прямом виде, т.е. нужно оставить целой перемычку прямого входа и пережечь перемычку инверсного входа:

- L — переменная входит в терм в инверсном виде, т.е. нужно сохранить перемычку у инверсного входа и пережечь у прямого;

- "—" — переменная не входит в терм и не должна влиять на него, т.е. нужно пережечь перемычки обоих входов.

Оставление перемычек у обоих входов переменной как бы устраняет из матрицы соответствующую схему И, поскольку в силу равенства хх = С выход этой схемы всегда нулевой и не влияет на работу матрицы ИЛИ на вход которой подается;

- А - указывается в выходном столбце (столбце функции) и свидетельствует о связи данной схемы И с выходом ПЛМ через матрицу ИЛИ. Пе­ремычка должна быть сохранена;

- "." — указывает на то, что данная схема И не подключается к выходу '.' должна иметь пережженную перемычку в матрице ИЛИ.

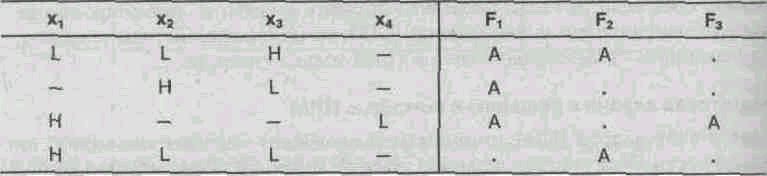
В принятой символике для программирования ПЛМ взятого ранее примера сведения будут заданы таблицей (табл. 1).

Таблица 1.1.

Упрощенное изображение схем ПЛМ

Схемы ПЛМ достаточно громоздки, и поэтому изображать их желательно с максимально возможным упрощением. Используются изображения, в кото­рых многовходовые элементы И, ИЛИ условно заменяются одновходовыми.

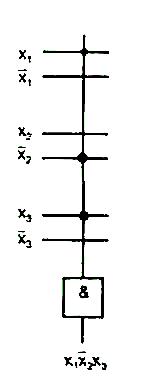
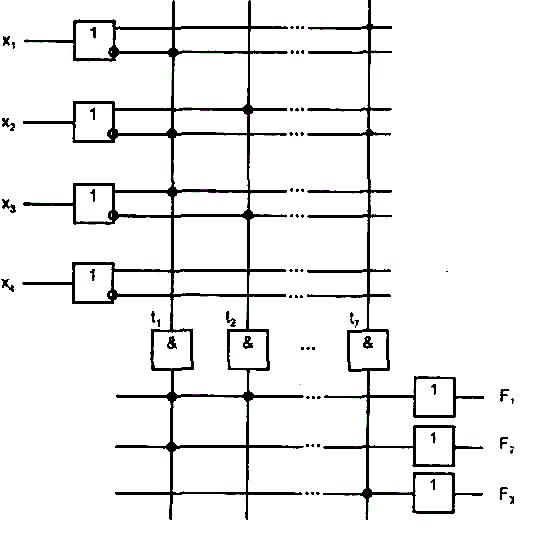
Рис. 1.4. Упрощенное изображение схемы многовходового логического элемента (а) и ПЛМ (б)

Единственная линия входа таких элементов пересекается с несколькими линиями входных переменных. Если пересечение отмечено точкой, данная переменная подается на вход изображаемого элемента, если точки нет, то переменная на элемент не подается. Пример многовходового конъюнктора с входами x1x2x3 показан на рис. 1.4, а. Схема рис. 1.2, а в новом упрощенном изображении имеет вид, приведенный на рис. 1.4, б.

Воспроизведение скобочных форм переключательных функций

С помощью ПЛМ можно воспроизводить не только дизъюнктивные нормальные формы переключательных функций, но и скобочные формы В этом случае сначала получают выражения в скобках, а затем они рассматриваются как аргументы для получения окончательного результата. В схеме появляются обратные связи — промежуточные результаты с выхода вновь подаются на входы, логическая глубина схемы увеличивается, задержка выработки результата растет. Пусть, например, требуется получить функцию:

Для этого следует применить включение ПЛМ по схеме (рис. 1.5).

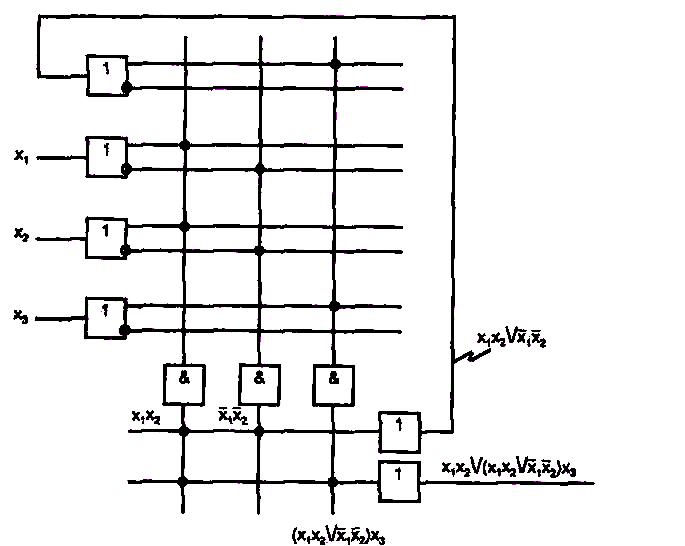
Рис. 1.5. Схема включения ПЛМ при воспроизведении скобочных форм переключательных функций

Наращивание (расширение) ПЛМ

Если размерность задачи превосходит возможности имеющихся ПЛМ, прихо­дится их наращивать. Когда число функций в системе N превосходит число выходов ПЛМ, несколько ПЛМ включаются параллельно по входам (рис. 1.6). На выходах каждой из ПЛМ воспроизводится часть функций. Общее число ПЛМ определяется как 1 N/n Г. Так как число термов предполагается достаточным (l- сист ^< l), все ПЛМ могут быть запрограммированы на одни и те же термы.

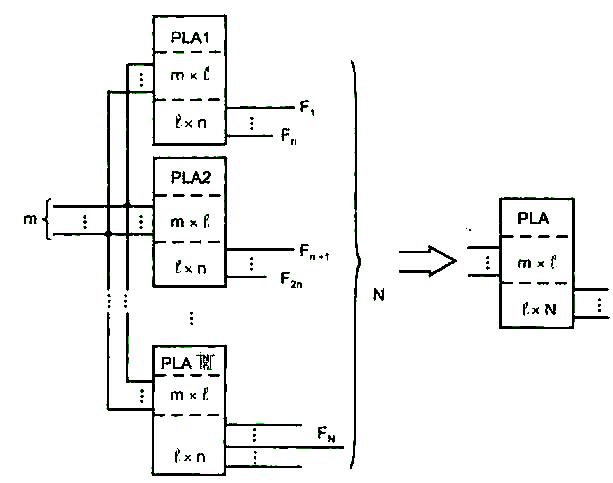
Рис. 1.6. Схема расширения ПЛМ по числу выходов

Если число термов системы l сист превышает число термов ПЛМ ( l сист> l), то к одной ПЛМ подключаются дополнительные с тем же числом входов и выходов. По входам ПЛМ включаются параллельно, а соответствующие выходы соединя­ются по ИЛИ или просто объединяются, если это выходы с третьим состоянием или возможностями монтажной логики. Каждая ПЛМ программируется на свои термы, затем из термов "собираются" на выходах нужные функции (рис. 1.7).

Расширение числа входов — наиболее сложная задача, связанная с декомпо­зицией системы функций. В частном случае, если все термы содержат не бо­лее m переменных, множество термов можно разбить на подмножества, содержащие не более m одинаковых переменных. Для реализации потребуется число ПЛМ, равное числу подмножеств, а выходы ПЛМ будут соединены так же, как и при расширении числа термов. Входными переменными каждой ПЛМ будут только связанные с образованием термов данного подмножества.

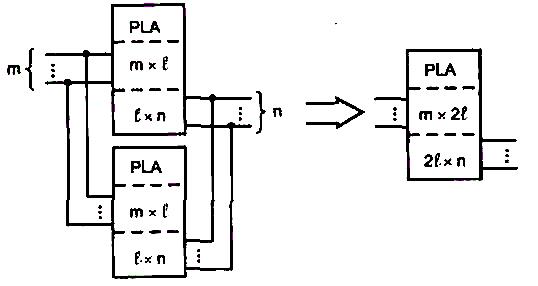
Рис. 1.7. Схема расширения ПЛМ по числу термов'

Часто в числе входных переменных ПЛМ имеются тактирующие сигналы взаимно исключающие друг друга в смысле одновременности вхождения в термы. Такие сигналы можно разделить на группы (подмножества), каждая из которых вместе с оставшимися переменными может обрабатываться отдель­ной ПЛМ (рис. 8).

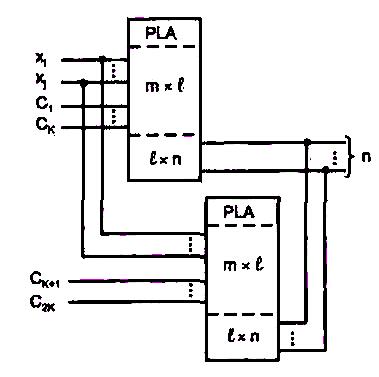
Рис. 1.8. Схема первого варианта расширения ПЛМ по числу входов

Стандартным приемом расширения ПЛМ по входам является перенос избыточного числа аргументов на предварительный дешифратор, выходы которого разрешают работу одной из ПЛМ, обрабатывающих оставшуюся часть аргументов. Этот прием рассматривался ранее применительно к наращиванию дешифраторов и других схем. Расширение числа входов ПЛМ на единицу, произведенное по такому методу, показано на рис. 1.9. Для значительного расширения числа входов этот прием мало пригоден, т. к. избыточные переменные образуют слова, подвергающиеся полной дешифрации, что резко увеличивает число ПЛМ в схеме (удваивает с добавлением каждого избыточного входа).

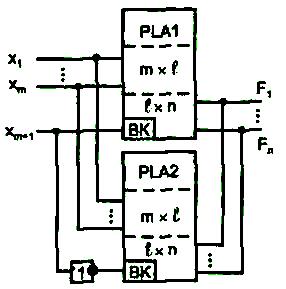
Рис. 1.9. Схема расширения числа входов ПЛМ на единицу

Простая эвристическая методика расширения ПЛМ по входам, не претендующая на оптимальность, предложена в работе [31] и описана также в [37].

Первые отечественные ПЛМ были выпущены в составе серии К556 (микросхемы РТ1, РТ2 схемотехнологии ТТЛШ с программированием прижиганием перемычек). Их размерность 16 входов, 48 термов, 8 выходов, задержка около 50 не. Микросхема РТ1 имеет выходы с открытым коллектором. Микросхема РТ2 имеет выходы с тремя состояниями.

Программируемая матричная логика

Одно из важных применений БИС программируемой логики — замена ИС малого и среднего уровня интеграции при реализации так называемой произвольной логики. В этих применениях логическая мощность ПЛМ зачастую используется неполно. Это проявляется, в частности, при воспроизведении типичных для практики систем переключательных функций, не имеющих больших пересечений друг с другом по одинаковым термам. В таких случаях возможность использования выходов любых конъюнкторов любыми дизъюнкторами (как предусмотрено в ПЛМ) становится излишним усложнением. Отказ от этой возможности означает отказ от программирования матрицы ИЛИ и приводит к структуре ПМЛ (PAL, GAL).

В ПМЛ (рис. 1.10) выходы элементов И (выходы первой матрицы) жестко распределены между элементами ИЛИ (входами матрицы ИЛИ). В показанной ПМЛ m входов, n выходов и 4n элементов И, поскольку каждому элементу ИЛИ придается по четыре конъюнктора.

В сравнении с ПЛМ схемы ПМЛ имеют меньшую функциональную гибкость, т. к. в них матрица ИЛИ фиксирована, но их изготовление и использование проще. Преимущества ПМЛ особенно проявляются при проектировании несложных устройств.

Подготовка задач к решению на ПМЛ имеет много общего с подходом к решению задач на ПЛМ, но есть и различия. Для ПМЛ важно уменьшить число элементов И для каждого выхода, но если для ПЛМ стремятся искать представление функции с наибольшим числом общих термов, то для ПМЛ это не требуется, поскольку элементы И фиксированы по своим выходам и. не могут быть использованы другими выходами (т. е. для других функций).

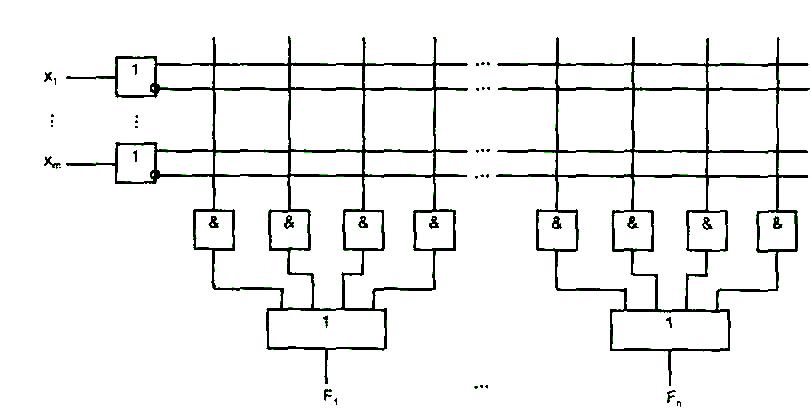
Рис. 1.10. Базовая структура ПМЛ

Функциональные разновидности ПЛМ и ПМЛ

Рассмотренные структуры ПЛМ и ПМЛ — базовые, с которых началось развитие этих направлений. В дальнейшем происходило обогащение функциональных возможностей ПЛМ и ПМЛ с помощью ряда приемов, в первую очередь следующих.

Схемы с программируемым выходным буфером

В этих схемах обеспечивается возможность получения выходных функций в прямом или инверсном виде. В такой схеме (рис. 1.11) выработанные матрицами функции Fi*...Fn* проходят через выходной буфер, разрядные схемы которого выполнены как сумматоры по модулю 2.

В показанной на рисунке схеме вторые входы сумматоров получают нулевые сигналы от потенциала "земли" через плавкие перемычки ПП. При этом Fj* = F; и функции с выхода матриц передаются через буфер без изменений. Если пережечь перемычку у нижнего входа сумматора, то он получит сигнал логической единицы от источника питания через резистор R. Складываясь по модулю 2 с единицей, функции Fi* инвертируются. Следовательно, в линиях с целыми перемычками функции проходят через буфер неизменными, а в линиях с отсутствующими перемычками — инвертируются.

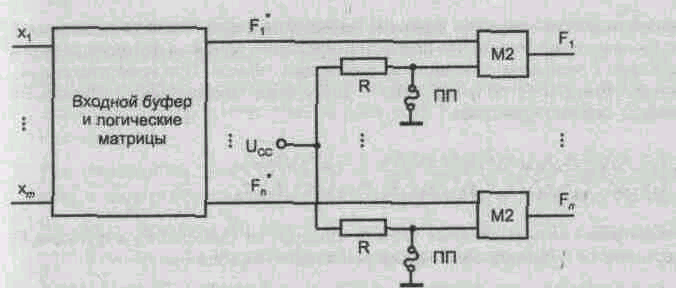
Рис. 1.11. Схема программируемого выходного буфера

Программируемый буфер дает дополнительные возможности для минимизации числа термов в реализуемой системе. В исходной системе можно заменять функции их инверсиями, если это приводит к уменьшению числа термов. Никаких последствий в смысле введения дополнительных схем это не вызовет — возврат к исходной системе будет обеспечен просто программированием буфера.

Пример

Пусть нужно воспроизвести систему из двух функций:

Карты Карно для этих функций (рис. 1.12) показывают контуры, соответствующие 8 различным термам системы:

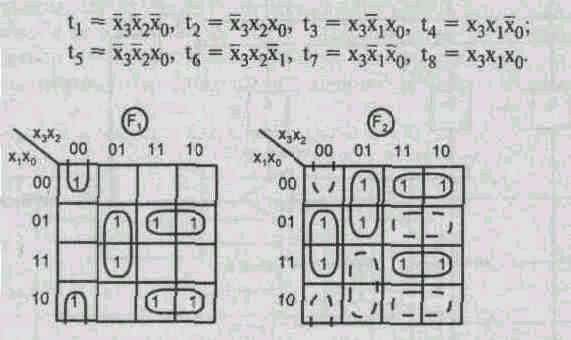
Рис. 1.12. Карты Карно для примера воспроизведения функций в ПЛМ с программируемым выходным буфером

При инвертировании функции единицы занимают в карте Карно те позиции, ко­торые были нулями. Видно, что при инвертировании одной из функций получим карты Карно с меньшим количеством различных термов. При инвертировании, например, функции Fz получим карту с контурами, показанными штриховыми линиями, и систему функций:

в которой всего пять различных термов. Возврат от функции F2 к функции F2 осуществляется пережиганием перемычки в линии выхода F2.

Схемы с двунаправленными выводами

Используя элементы с тремя состояниями выхода, можно построить схему, в которой некоторые выводы можно приспосабливать для работы в качестве входов или выходов в зависимости от программирования перемычек. В такой схеме один из конъюнкторов предназначен для управления элементом с тремя состояниями выхода (рис. 13). Выход элемента одновременно связан с матрицей И как вход.

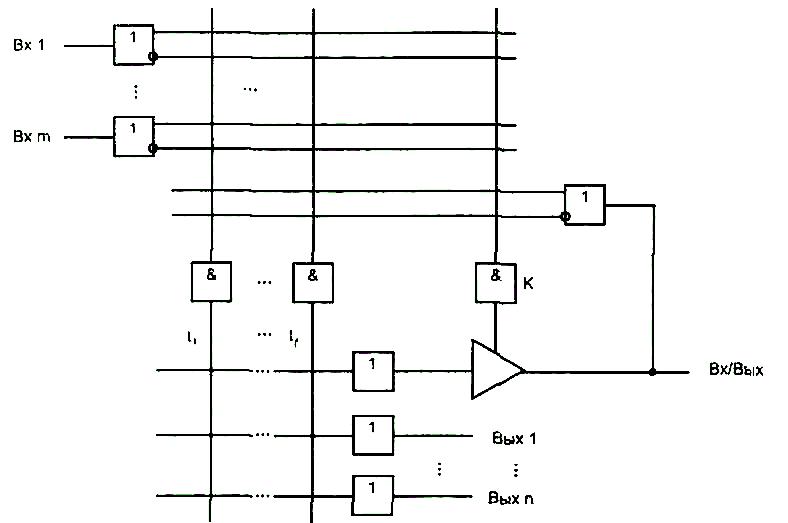
Рис. 1.13. Схема с двунаправленным буфером

Возможны четыре режима вывода Вх/Вых в зависимости от того, как запрограммированы входы конъюнктора К:

1. Все перемычки нетронуты. В этом режиме на выходе конъюнктора К будет нуль, буфер имеет третье состояние выхода и вывод функционирует как вход.

2. Все перемычки пережжены, на выходе конъюнктора единица, буфер активен, вывод работает как выход (его сигналы не используются в матрице И).

3. Выход с обратной связью. Этот режим отличается от предыдущего только тем, что сигналы вывода используются в матрице И.

4. Управляемый выход. Здесь входы конъюнктора программируются. При заданной комбинации входных сигналов конъюнктор приобретает единичный выход, и вывод срабатывает как выход.

В схеме с некоторым числом двунаправленных выводов можно изменять соотношение числа входов-выходов. Если число входов равно т, число выходов n и число двусторонних выводов р, то можно иметь число входов от m до m + р и число выходов от п до п + р при условии, что сумма числа входов и выходов не превосходит m + п + р.