2.Доверительные интервалы для оценки математического ожидания случайной величины х, имеющей нормальное распределение при неизвестном среднем квадратичном отклонении

Интервальные оценки позволяют установить и надежность оценки. Доверительным называют интервал (θ*-δ; θ*+δ), который покрывает неизвестный параметр с заданной надежностью γ. Пусть задана генеральная совокупность с нормальным распределением признака Х, причем среднее квадратичное отклонение σ неизвестно. По данным выборки можно построить СВ (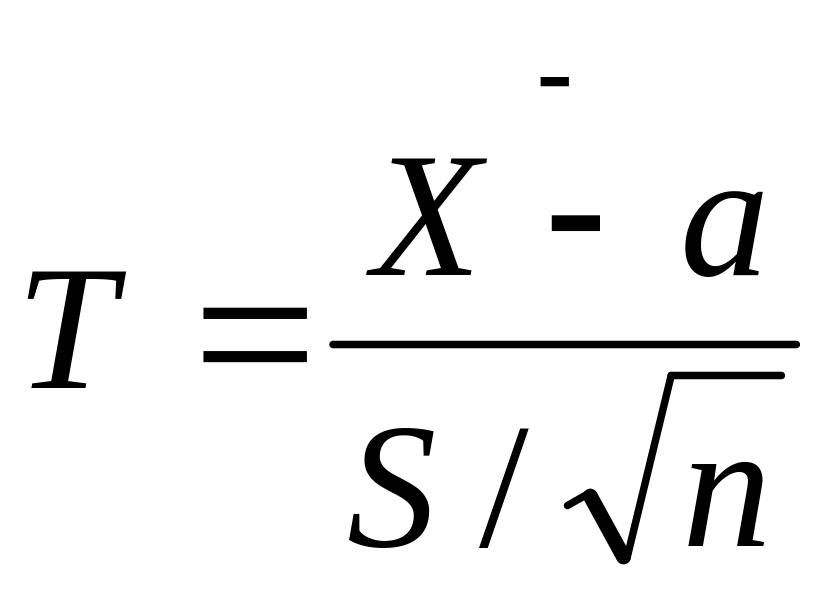 ), которая имеет распределение Стьюдента с k=n-1 степенями свободы, где - выборочная средняя, S – «исправленное» среднее квадратичное отклонение, n – объем выборки. Плотность распределения Стьюдента: , где , где распределение Стьюдента определяется параметром n и не зависит от неизвестных параметров a и σ – является большим достоинством, т.к. S(t,n) – четная функция от t, вероятность осуществления неравенства 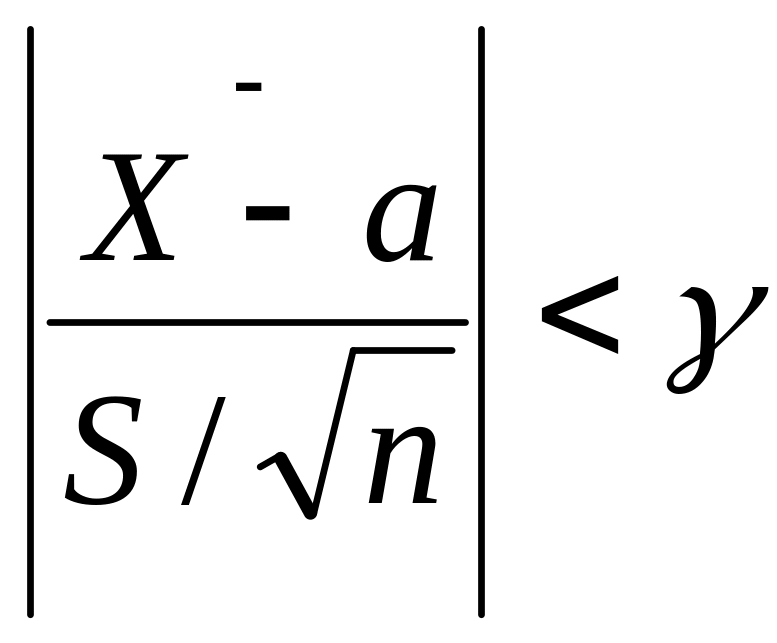определяется: , в последствии получаем:

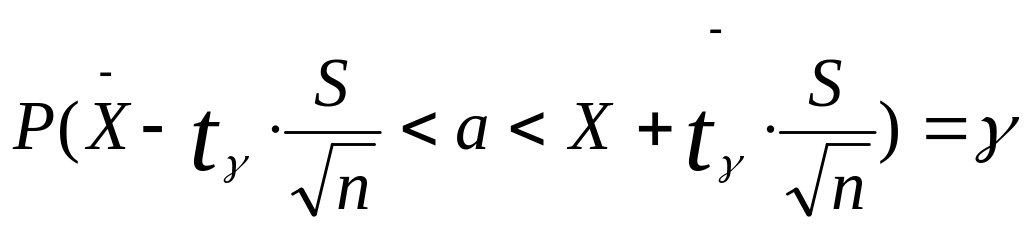
Пользуясь распределением Стьюдента, находим доверительный интервал, покрывающий неизвестный параметр а с надежностью γ. По заданным n и γ находим t_γ. Распределение Стьюдента при малой выборке дает широкий доверительный интервал, что говорит о малом содержании интересующей нас информации о признаке.

№ 15

1. Нормальное распределение. Плотность нормального распределения и ее свойства. Нормированное (стандартное) нормальное распределение.

Нормальным называют распределение вероятностей непрерывной случайной величины, кот описывается плотностью. Плотность распределения определяется следующим выражением:

г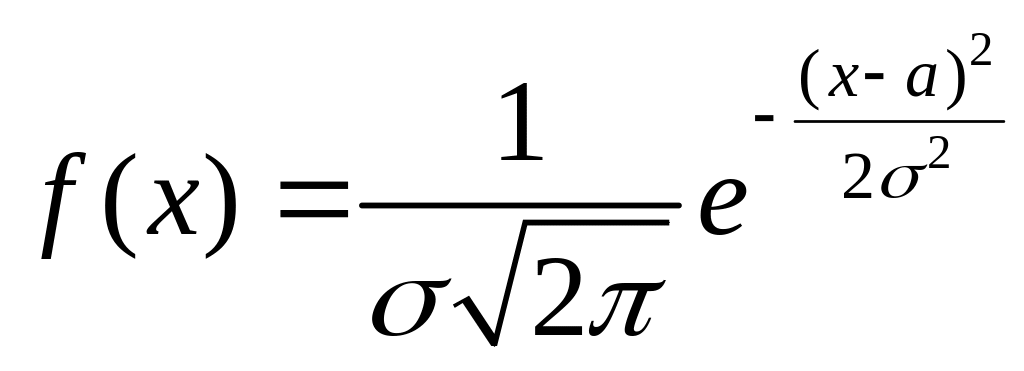 де а – математическое ожидание, σ – среднее квадратическое отклонение нормального распределения.

а= М(х), σ = √D(x).

Св-ва плотности: 1) она положительна, т.е f(x)≥0;

2) ∫f(x)dx = 1 – несобственный интеграл от плотности распределения в пределах от -∞ до ∞ = 1.

Нормированным называют нормальное распределение с параметрами а = 0 и σ = 1. Например, если х – нормальная величина с параметрами а и σ, то U =(x-a)/σ – нормированная нормальная величина, причем М(U) = 0, σ(U) = 1.

1. Интегральные оценки. Точность оценки. Доверительная вероятность.

Интегральной называют оценку, кот определяется двумя числами – концами интервала. Она позволяет установить точность и надежность оценок.

Пусть θ* служит оценкой неизвестного параметра θ. Ясно, что θ* тем точнее определяет параметр θ, чем меньше абсолютная величина разности | θ – θ* |, т.е. если δ>0 и | θ – θ* | < δ , то чем меньше δ, тем оценка точнее → положительное число δ характеризует точность оценки.

Доверительной вероятностью оценки θ по θ* называется вероятность γ, с которой осуществляется неравенство | θ – θ* | < δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к 1 (0,95; 0,99).

№ 13 Если попадется этот билет, лучше поменяйте!!!

1. Непрерывные случайные величины. Дифференциальная и интегральная функции их распределения, их смысл и связь между ними.

Непрерывной называют случайную величину, кот может принять все значения из некоторого конечного или бесконечного промежутка.

Функцией распределения случайной величины Х называется функция F(x), выражающая вероятность того, что Х примет значение строго меньше, чем х:

F(x)= P(X<x).

Плотностью распределения непрерывной случайной величины называется функция f(x)= F'(x). Плотность распределения любой случайной величины неотрицательна, f(x)≥0, и обладает свойством ∫f(x)dx = 1.