2.Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область. Область принятия гипотезы. Критические точки.

Статистическим критерием называется СВ К, кот. служит для проверки нулевой гипотезы. Если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия К принимают отношение исправленных выборочных дисперсий: .

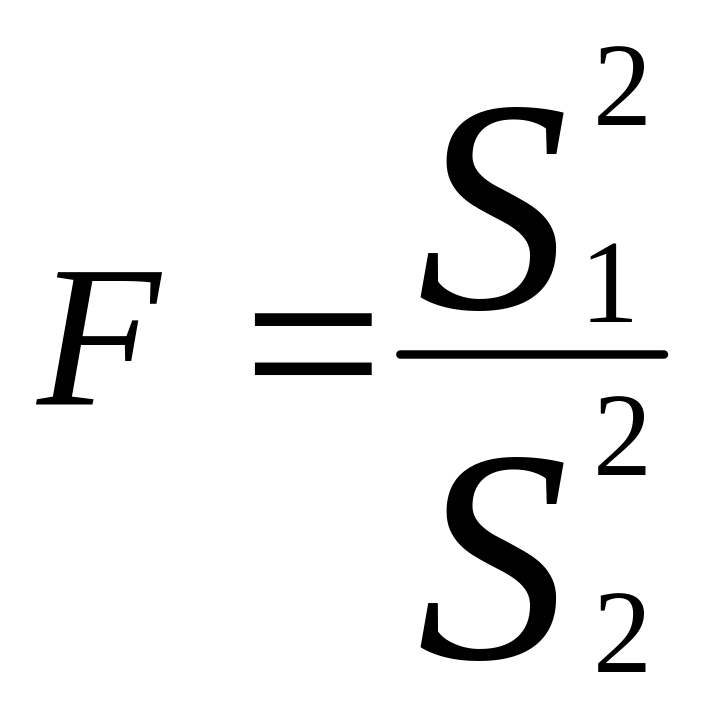Наблюдаемым значением К_набл. называют значение критерия, вычисленное по выборкам: .

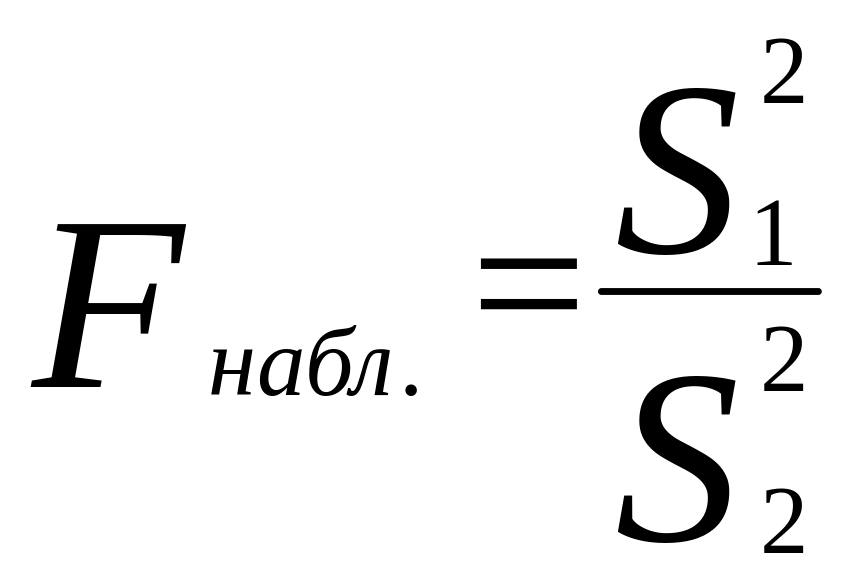Критической областью называют совокупность значений критерия, при кот. нулевую гипотезу отвергают. Областью критерия гипотезы называют совокупность значений критерия, при которых гипотезу принимают.

Критическая область и область принятия гипотезы являются интервалами, т.к. все значения критерия К принадлежат некоторому интервалу, следовательно, существуют точки, которые их разделяют.

Критическими точками k_кр. называют точки, отделяющие критическую область от области принятия гипотезы. Различают одностороннюю (право- или левостороннюю) и двустороннюю критическую область (может быть симметричной при ):

K>kкр, где kкр>0 K<kкр, где kкр<0

K<k1 и K>k2, где k2>k1

Билет 11

1.Распределение Пуассона.

Пусть n независимых испытаний, вероятность равна р;чтобы узнать сколько раз оно появится используем формулу Пуассона, но р≤0,1 и прибегают к этой формуле; при дополнительном предположении np=λ, где n – число испытаний, а λ постоянна; k – число появлений события в испытании: 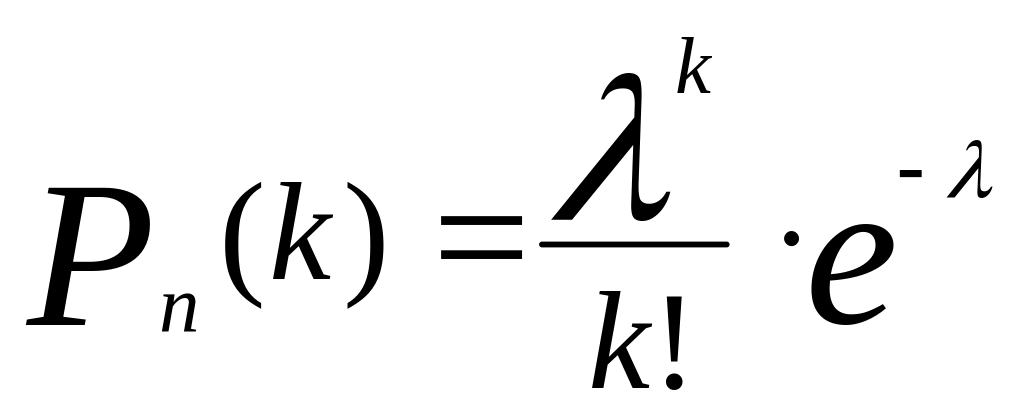, где k=0, 1, 2, …

Применяют при массовом событии, когда n велико; и редких событий когда р мало.

2.Статистические оценки параметров распределения (сущность теории оценивания): несмещенность, состоятельность, эффективность оценок.

Пусть СВ, характеризующая признак генеральной совокупности имеет некоторое распределение, вид которого известен, тогда возникает задача оценки параметра этого распределения.

Статистическая оценка неизвестного параметра – фун-ия от наблюденных случайных величин. Для того, чтобы статист.оценки давали хорошее приближение оцениваемых параметров, они должны удовлетворять определенным требованиям:

Θ – некий параметр генеральной совокупности

Θ* - некий параметр оценки параметра

Если Θ* построена так, что дает значение с превышением, истинная оценка тоже будет с превышением, и наоборот.

Несмещенная статистическая оценка – если ее мат. Ожидание равно ожениваемому параметру при любом объеме выборки: М(Θ*)= Θ. Стремятся так строить статист. оценку, чтобы ее дисперсия была минимальной.

Эффективная статист. оценка – при заданном объеме выборки имеет минимальную возможную дисперсию. «Хорошая» статист.оценка должна обладать св-вом состоятельности, т.е. при n→∞ стремится по вероятности к оцениваемому параметру: , n→∞

Билет 12

1.Дисперсия и среднее квадратическое отклонение случайной величины. Свойства дисперсии.

Дисперсией (рассеянием) дискретной СВ называют мат.ожидание квадрата отклонения СВ от ее мат.ожидания: . Пусть СВ задана законом распределения

Х	х1	х2	…	хn
Р	р1	р2	…	pn

Тогда квадрат отклонения имеет следующий закон распределения:

			…
Р	р1	р2	…	pn

По определению дисперсии, Дисперсия равна разности между мат.ожиданием квадрата СВ Х и квадратом ее мат.ожидания: , т.е. Средним квадратичным отклонением СВ Х называют квадратный корень из дисперсии: ; в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность СВ, вычисляют среднее квадратичное отклонение, а не дисперсию.

Свойства дисперсии:

1)дисперсия постоянной величины С равна нулю: D(C)=0;

2)постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СХ)=С²∙D(X);

3)дисперсия суммы двух независимых СВ равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y);

4)дисперсия разности двух независимых СВ равна сумме их дисперсий: D(X-Y)=D(X)+D(Y)