1.Биномиальное распределение. Наивероятнейшее число наступления событий

Пусть производится n независимых испытаний, в каждом из кот. событие А может появиться, а может и не появиться. Вероятность наступления события постоянна и равна р, причем q=1-p – это вероятность непоявления события.

Рассмотрим в качестве в качестве дискретной СВ Х число появлений события А в этих испытаниях. Ставится задача, найти закон распределения, т.е. определить возможные значения Х и его вероятности. В n испытаниях событие А может появиться 0, 1, 2, 3…n раз, т.е. х₁=0, х₂=1, х₃=2…х_n+1=n. Для нахождения вероятности воспользуемся формулой Бернулли: , где k=0,1,2,… Эта формула и выражает искомый закон распределения.

Биномиальное распределение – это распределение вероятностей, определяемое законом Бернулли.

Правую часть можно рассматривать, как общий член разложения бинома Ньютона.

Наивероятнейшее значение μ появления события равно целой части числа: ; а при целом наибольшее значение вероятности достигает в двух случаях: и

2.Статистическая проверка гипотез. Статистическая гипотеза: нулевая и альтернативная, параметрическая и непараметрическая, простая и сложная. Ошибки 1 и 2 рода.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Нулевой называют выдвинутую гипотезу Н_0.

Альтернативная гипотеза – гипотеза Н₁, кот. противоречит нулевой.

Н₀: а=5, Н₁: а≠5

Простая гипотеза – гипотеза содержащая одно предположение.

Сложная гипотеза – состоит из конечного или бесконечного числа простых гипотез. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. ошибки 2х родов:

Ошибка 1го рода состоит в том, что будет отвергнута правильная гипотеза;

Ошибка 2го рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку 1го рода принято обозначать через α – уровень значимости. В 0,01 случае из 100 можно совершить ошибку 1го рода.

Билет 9

1.Равномерное распределение. Определение константы, математического ожидания, дисперсии.

Непрерывную случайную величину можно задать используя фун-ию, кот. называют плотностью распределения. Плотностью распределения вероятностей непрерывной СВ Х называют фун-ию f(x) – первую производную от фун-ии распределения F(x):

Для дискретной СВ плотность распределения неприменима.

Вероятность того, что непрерывная СВ Х примет значение, принадлежащие интервалу (а;b) равна определенному интегралу от плотности распределения, взятому в пределах от а до b: .

Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения СВ, плотность распределения сохраняет постоянное значение:

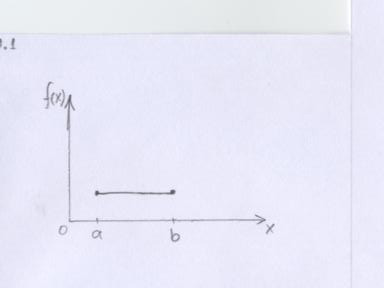
Математическим ожиданием непрерывной СВ Х, выраженное значение которой принадлежит отрезку [а;b] называют определенный интеграл: . Дисперсией непрерывной СВ называют математическое ожидание квадрата ее отклонения: