2.Моменты (начальные и центральные). Показатели асимметрии и эксцесса.

Моменты – дополнительные числовые характеристики с/в. Начальный момент порядка k с/в x – это математическое ожидание величины x^k:

ν_k=M(x^k).

Для дискретной и непрерывной с/в ν_k[x] вычисляются по формулам:

Центральный момент порядка k с/в x – математическое ожидание величины [Х-М(х)]^k:

μ_k=M[x-M(x)]^k.

Моменты, определения которых были даны выше, называют теоретическими. Они связаны с возможными значениями и вероятностными. Кроме них есть ещё эмпирические моменты – вычисляются по данным наблюдений.

Ассиметрия выборочного распределения – отношение центрального момента третьего порядка к кубу среднего квадратического отклонениея:

, где μ₃ – центральный статистический момент третьего порядка, вычисляемый по формуле: . Если распределение симметричное, то A_s=0.

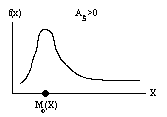
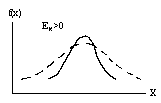
Для оценки крутости, т.е. большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой - эксцессом. Эксцесс выборочного распределения – характеристика, которая определяется равенством центрального момента четвёртого порядка к четвёртой степени среднего квадратического отклонения:

Е_k= (μ₄/ σ_в⁴)-3. Здесь μ₄ – центральный статистический момент четвёртого порядка, вычисляемый по формуле: μ₄=∑_i (x_i-X)(m_i/n)

Экзаменационный билет № 22

1.Вариационный ряд. Показатели изменчивости: вариационный размах, среднее линейное отклонение, дисперсия, коэффициент вариации.

Пускай из генеральной совокупности была осуществлена выборка и получены следующие значения:

х1	n1
х2	n2
xi	ni

∑ n_i=n – объём выборки

Наблюдаемые значения x_i – это варианты. Ряд x_i, выстроенный по возрастанию – это вариационный ряд.

n_i – частоты. w_i=n_i/n – относительная частота.

Вариационный размах (R) – это разность м/у наибольшей и наименьшей вариантами.

R=x_max-x_min Пр.: для ряда 1 3 4 6 10 R=10-1=9

Среднее линейное отклонение - средняя арифметическая произведений абсолютных величин отклонений вариантов признака x_j от среднего арифметического и соответствующих им частот mx_j (wx_j)

,         ,        

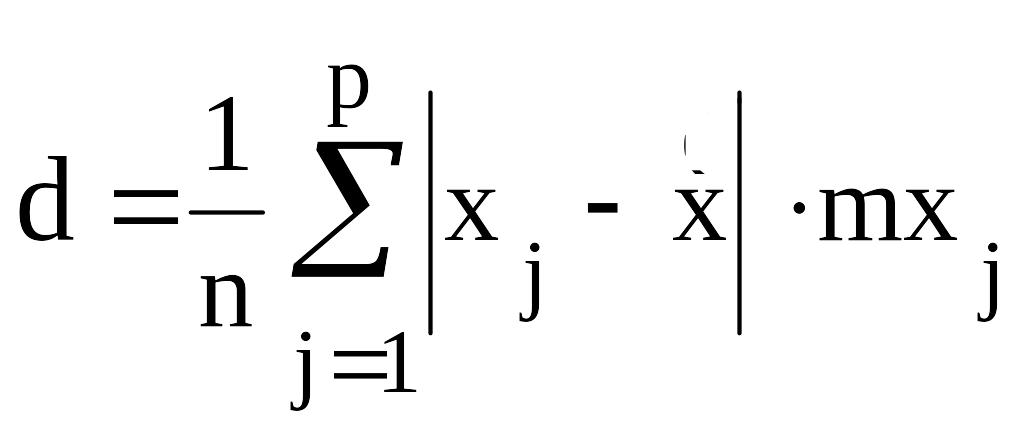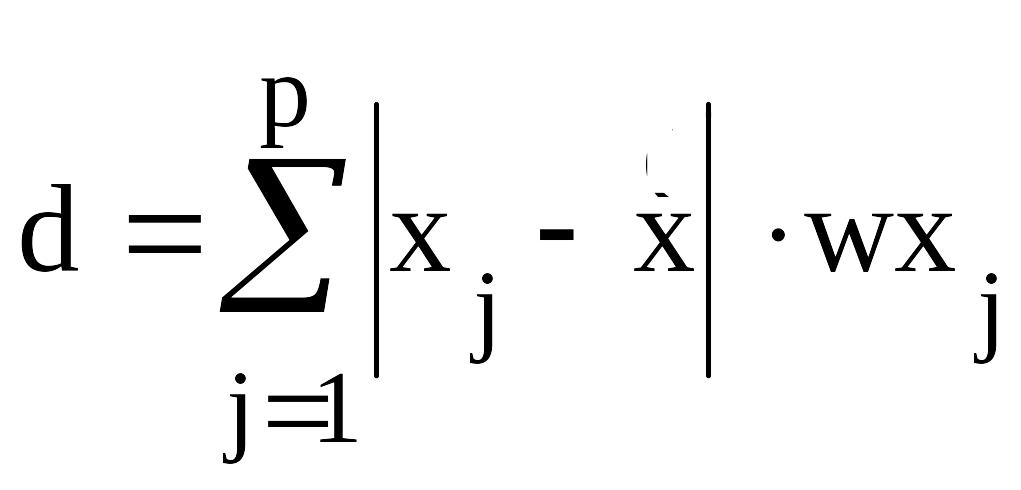Среднее абсолютное отклонение – среднее арифметическое абсолютных отклонений (θ). Служит для характеристики рассеяния вариационного ряда.

. Например, для ряда имеем:

,

Коэффициент вариации (V) – выраженное в % отношение выборочного среднего квадратического отклонения к выборочной средней:

Дисперсия D_в=σ_в² вариационного ряда называется среднее арифметическое квадратов отклонения вариант от их средней: .

2.Доверительные интервалы для оценки математического ожидания случайной величины X, имеющей нормальное распределение при неизвестном параметре σ.

Доверительным называют интервал, который с заданной надежностью γ покрывает заданный параметр.

Заданы генеральная совокупность с нормальным распределением признака Х. Причём среднее квадратическое σ(х) известно. Требуется оценить, в смысле интервальной оценки, неизвестное математическое ожидание а по выборочной средней . Т.е. мы должны найти доверительный интервал, покрывающий параметр с надежностью γ.

Можно рассматривать выборочную среднюю как с/в и выборочные значения (элементы выборки признака х₁, х₂, х₃..x_n) как одинаково распределенные случайные величины Х₁, Х₂, Х₃..Х_n, т.е. математическое ожидание каждой из этих величин равно а, а среднее квадратическое равно σ.

Будем считать, что если с/в Х распределена нормально, то выборочное среднее , найденной по независимым наблюдениям, также распределено нормально.

А параметры распределения мы уже находили: М( )=а, D( )=D/n, σ( )=σ/√n.

Потребуем, чтобы выполнялось соотношение:

Решение:

Вместо σ и Х подставляем σ/√n и :

->

С надежностью γ доверительный интервал покрывает неизвестный параметр а. Точность оценки