1. Вероятность попадания нормально распределенной св в заданный интервал. Вероятность заданного отклонения нормальной св от своего математ.Ожидания. Правило трех сигм

1) Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а;b) равна определенному интегралу от плотности распределения, взятому в пределах от a до b

2) Если 2-е случайные величины нормально распределены и а=0, то вероятность принять значение, принадлежащие интервалу (-δ, δ) больше у той величины, которая имеет меньше значения σ. σ характеризует рассеяние нормальной случайной величины вокруг ее математического ожидания

3) Правило 3-х сигм:

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратного отклонения.

Т.е. если распределение случайной величины неизвестно, но условие 3-х сигм выполняется, то есть основание предполагать, что изученная величина распределена нормально.

2.Точечная оценка генеральной дисперсии. «Исправленные» выборочная дисперсия и среднее квадратичное отклонение

1) Выборочная дисперсия - это среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения

- если все значения признака выборки объема n различны, то

- если значение признака имеют соотв. частоты , причем , то

Пример:

Решение: найдем

найдем

2) Выборочным средним квадратическим отклонением, называют квадратный корень из выборочной дисперсии:

3) Точечной оценкой генеральной дисперсии называют оценку, которая определяется одним числом.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию

Билет №17

1.Закон больших чисел. Понятие о теореме Чебышева. Значение теоремы Чебышева. Теорема Бернулли

К закону больших чисел относятся теоремы Чебышева и Бернулли, а так же другие теоремы

1) Теорема Чебышева:

- если - попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа с), то как бы мало не было положительное число ε, вероятность неравенства

Будет как угодно близка к единице, если число случайных величин достаточно велико.

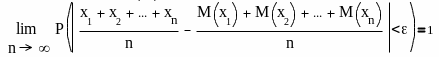
т.е. если рассматривается довольно большое число независимых случайных величин имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящие в том, что отклонение ср. арифм. Их математических ожиданий будет по абсолютной величине сколько угодно малым.

- если - попарно независимые случайные величины, имеющие одно и то же математическое ожидание а , и если дисперсии этих величин равномерно ограничены, то как бы мало не было число ε>0, вероятность неравенства , будет как угодно близка к 1, если число случайных величин достаточно велико.

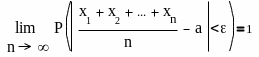
2) Теорема Бернулли

- получила название закона больших чисел.

Если в каждом из n независимых испытаний вероятность Р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности Р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Т.е. если ε – малое положительное число, то при соблюдении условий теоремы имеет место равенство