Рішення закритої моделі транспортної задачі.
План перевезень називається припустимим, якщо величини хij задовольняють наступним обмеженням:
обмеження по ресурсах
(4)
обмеження по потребах
5)
умови незаперечності:
(6)
Перші m рівностей означають, що з кожного пункту відправлення вивозиться весь наявний вантаж, а наступні п рівностей означають повне задоволення кожного пункту призначення.
Під час перевезення неподільних вантажів модель транспортної задачі містить ще одне обмеження на шукані величини xij: вони повинні бути цілими числами.
Транспортна задача описується цільовою функцією:
(7)
що відповідає сумарним витратам на перевезення.
Рішення задачі зводиться до мінімізації цієї цільової функції для усіх величин хij, що задовольняють умовам (4)–(6).
Рішення відкритої моделі транспортної задачі.
У випадку перевищення сумарних ресурсів над сумарними потребами (2) для визначення оптимального плану перевезень уводять фіктивний (п+1)-й пункт призначення з потребою
і покладають вартості m перевезень вантажів у цей пункт рівними нулю:
Отримана задача перетворюється в закриту транспортну задачу, тому що для неї виконується рівність
Для визначення оптимального плану перевезень у випадку перевищення сумарних потреб над сумарними ресурсами (3) вводиться фіктивний (m+1)-й пункт відправлення вантажу, запас якого дорівнює
і вартості n перевезень вантажів з цього пункту приймаються рівними нулю:
Нова задача є вже закритою транспортною задачею, тому що для неї виконується рівність
Слід зазначити, що для випадку відкритої задачі цільова функція Z також буде визначатися формулою (7), тому що вартості перевезень вантажів з фіктивного пункту відправлення чи вантажу у фіктивний пункт призначення по визначенню дорівнюють нулю.
Висновок.
Уведення фіктивних пунктів відправлення чи вантажу призначення зводить відкриту задачу до закритої, що дозволяє уніфікувати підхід до рішення транспортних задач.
З уведенням фіктивного пункту призначення в оптимальному плані основні змінні покажуть раціональні маршрути й обсяги перевезень у них, а змінні, пов'язані з фіктивним пунктом споживання, — не перевезений залишок запасів.
Аналогічно з уведенням фіктивного пункту відправлення вантажу в оптимальному плані, основні змінні покажуть раціональні маршрути й обсяги перевезень у них, а змінні, пов'язані з фіктивним пунктом відправлення, покажуть незадоволений попит.
Тепер розглянемо можливості надбудови «Пошук рішення» MS Excel (дивися практичне заняття: Тема 2, Заняття 4, 3 питання) при визначенні оптимального плану перевезень, як для випадку закритої транспортної задачі, так і для двох варіантів відкритої.
1. Підготовка та введення даних. Задача 1
На трьох складах A, B, C є 65, 80 і 105 тонн бензину відповідно. Потрібно скласти план його перевезення до чотирьох споживачів (I, II, III, IV) так, щоб вони одержали необхідні 45, 60, 80 і 65 тонн бензину відповідно, а витрати на перевезення були мінімальними. Вартість перевезення 1 тонни бензину (у гривнях) зі складів до споживачів подана у таблиці
Склади |
Споживачі |
|||
|
I |
II |
III |
IV |
A |
4 |
5 |
7 |
3 |
B |
5 |
3 |
4 |
5 |
C |
3 |
6 |
5 |
4 |
Рішення
Нехай
– матриця,
що визначає
план перевезень;
– матриця
транспортних
витрат;
а={65 80 105} — вектор ресурсів складів А, В, С;
b={45 60 80 65} — вектор потреб споживачів I, II, III, IV
Ця транспортна задача є закритою, тому що сумарні ресурси і сумарні потреби збігаються:
Сформулюємо математичну модель задачі.
1. Цільова функція, що відповідає сумарним витратам на перевезення бензину зі складів споживачам, має вигляд
(8)
2. При цьому задача має наступні обмеження:
обмеження по ресурсах
(9)
обмеження по потребах:
(10)
умови невід’ємності:
(11)
Таким чином, рішення транспортної задачі зводиться до мінімізації цільової функції (8) для усіх величин xij, що задовольняють умовам (9)-(11).
Перейдемо до реалізації задачі в Excel, робочий лист якого з усією необхідною інформацією показаний на рис. 1.
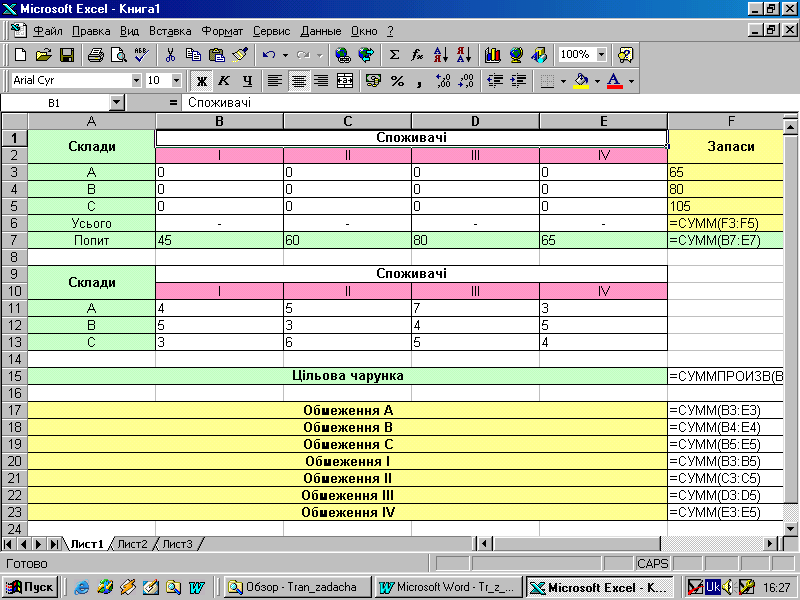
Рис. 1 Початкова таблиця задачі 1
Формується він у такий спосіб — у діапазон осередків ВЗ:Е5 як початкові значення попереднього розподілу запасів бензину на складах А, B, C між споживачами I, II, III, IV заносимо нулі. У діапазон осередків F3:F5 записуємо запаси бензину, розміщені на складах А, B, C відповідно. У діапазон осередків B7:Е7 — потреби в бензині споживачів I, II, III, IV.
В осередок F6 заносимо контрольну суму обсягів бензину, розміщеного на складах, тобто суму осередків F3:F5. В осередок F7 заносимо контрольну суму потреби в бензині всіх споживачів, тобто суму осередків B7:Е7. Оскільки розглянута модель транспортної задачі закрита, контрольні суми в осередках F6 і F7 повинні збігатися.
У діапазоні осередків B11:Е13 формуємо матрицю вартостей (витрат) перевезень однієї тонни бензину з кожного складу кожному споживачу.
Далі в осередок F15 заносимо формулу для розрахунку цільової функції, використовуючи вбудовану функцію =СУММПРОИЗВ(B11:Е13;ВЗ:Е5). Обмеження задачі записуються в осередки FI7:F23, куди вводяться функції, що відповідають вираженням лівих частин обмежень (9), (10).
Для обмеження А заносимо в осередок F17 сумарну кількість бензину, що буде перевезено зі складу А всіх споживачів, скориставшись убудованою функцією СУММ.
Для обмежень B, C вміст осередку F17 копіюється в осередки F18, F19.
Для обмеження I заносимо в осередок F20 сумарну кількість бензину, що доставляється першому споживачу з усіх складів. Для цього встановлюємо курсор в осередок F20 і уводимо формулу, що має вигляд = СУММ(ВЗ:B5).
Аналогічно заповнюються осередки F20:F23 для обмежень II—IV.
Р езультат представлений на рис. 2.
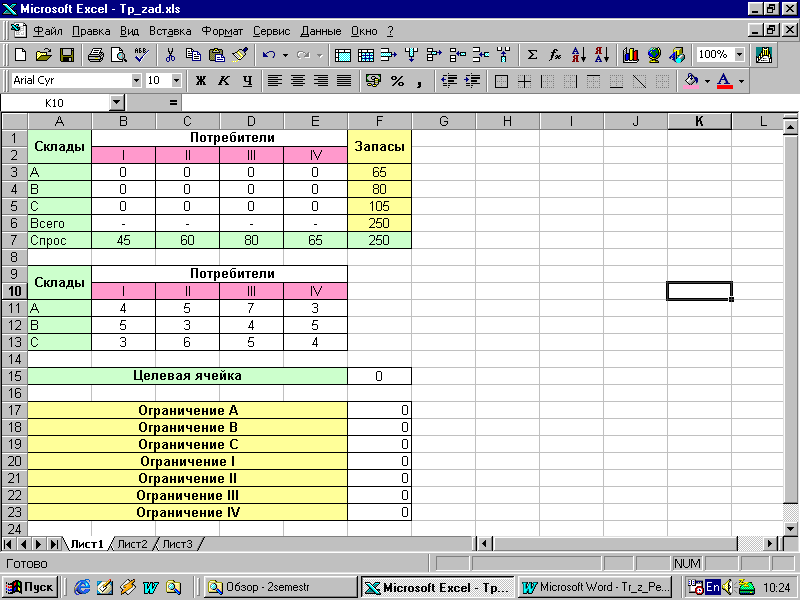
Рис 2. Зміст осередків початкової таблиці задачі 1