Ускорение

Если скорость v показывает, как изменяется радиус-вектор r точки со временем, то ускорение w показывает, как изменяется скорость v точки. Повторив предыдущие рассуждения, можно прийти к следующим определениям ускорений.

Мгновенным ускорением w называется предел отношения приращения скорости v к промежутку времени Dt, за который произошло это приращение, при стремлении Dt к нулю:

. (3.9)

Более краткая формулировка: мгновенное ускорение это производная скорости по времени.

Используем выражения (3.4) и (2.2) для записи ускорения w:

.(3.10)

Первое слагаемое в этом выражении w_ – вектор, направленный по скоростиv, и по модулю равный изменению скорости по абсолютной величине (см. рис 3.2) . Эта составляющая ускорения называется тангенциальным ускорением.

Второе слагаемое w_n отвечает за изменение скорости по направлению и называется нормальным ускорением. Найдем модуль и направление этого вектора следующим образом.

Для того чтобы вычислить нормальное ускорение необходимо вычислить производную . Ортe_ может изменяется только по направлению, что соответствует движению точки по искривленной траектории.

Каждому бесконечно малому участку искривленной траектории можно сопоставить окружность радиуса R, которая сливается с ним на этом участке. Радиус этой окружности характеризует кривизну траектории в данной точке. Поэтому движение точки на криволинейном бесконечно малом отрезке траектории можно представить как движение по окружности радиуса R.

При движении точки по окружности вектор ее скорости и соответственно орт скорости е_ вращаются с некоторой угловой скоростью .

Как мы показали (2.13), производная вращающегося, постоянного по модулю вектора равна:е_t. Таким образом, эта производная будет определять направление нормального ускорения. Направление единичного вектора совпадающегопо направлению с вектором w´е_t называется главной нормалью.

Таким образом, нормальное ускорение w_n будет равно

´ vе_t = v. (3.11)

Из элементарного курса физики известно, что модуль угловой скорости точки при ее движении по окружности связан с модулем скорости соотношением:  = v/R. Следовательно, модуль нормального ускорения будет равен: .

Модуль полного ускорения равен:

.(3.12)

Для того чтобы представить вектор ускорения w в декартовой системе координат нужно в выражении (3.9) скорость точки v записать в координатном виде. Получим:

w(t) =.

§4. Задачи кинематики.

Различают прямую и обратную задачи кинематики. Прямая задача кинематики состоит в том, чтобы по заданному положению точки определить остальные кинематические параметры – скорость и ускорение.

Под обратной задачей кинематики понимают нахождение кинематических параметров по известному ускорению w(t). Для решения этой задачи одного знания ускорения w(t) недостаточно. Необходимо еще знать начальные значения скорости v₀ и положения r₀ движущейся точки.

Наибольший интерес представляет собой обратная задача.

Из определения ускорения (3.9) следует илиw(t)dt = dv, где dv – приращение скорости точки за время dt. Проинтегрируем обе части этого равенства: .

За конечный промежуток времени изменение скорости от v₀ до v(t) будет очевидно равно сумме всех приращений dv, т.е. 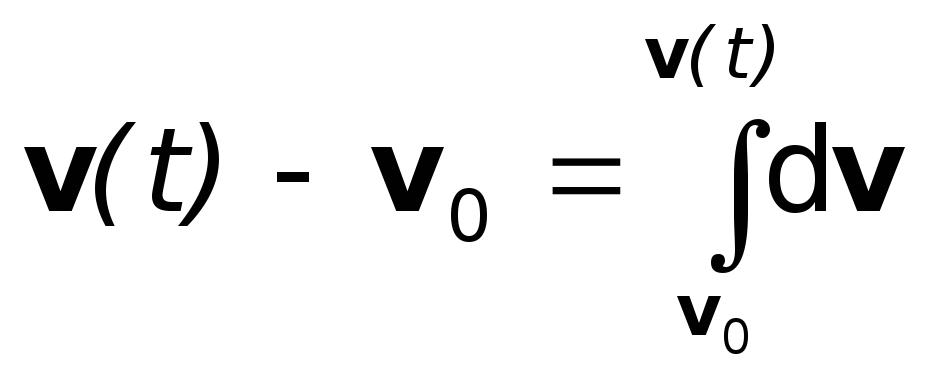. Окончательно имеем:

. (4.1)

Положение точки r(t) находится аналогично.

Из определения скорости (3.3) следует: v(t)×dt = dr. Проинтегрировав обе части этого равенства, получим:

. (4.2)

Покажите самостоятельно, что путь S, пройденный точкой равен:

.(4.3)

В качестве примера рассмотрим самый простой тип движения, а именно, движение с постоянным ускорением.

w(t) = const = w. (4.4)

Такое движение называется равнопеременным движением. В этом случае зависимости остальных кинематических параметров от времени вычислим по соотношениям 4.1 и 4.2.

v(t) = v₀ + wt; (4.5)

r(t) = r₀ + v₀t + wt²/2. (4.6)

В этих выражениях:

r(t)- положение точки в момент времени t;

r₀- положение точки в момент времени t = 0 (начальное положение);

v(t)- скорость точки в момент времени t;

v₀- скорость точки в момент времени t = 0 (начальная скорость).

Выражения (4.4  4.6) называются кинематическими уравнениями равнопеременного движения.

Если из условий задачи выясняется, что точка движется с постоянным ускорением w, то ее движение будет подчиняться уравнениям (4.5 – 4.6).

Примеры.

Пример 1. В некоторый момент времени точка имеет скорость v и ускорение w. Выразить тангенциальное w_ и нормальное w_n ускорения через эти кинематические параметры.

Решение

По определению (3.10) направление вектора тангенциального ускорения w_ совпадает с направлением вектора скоростиv и, следовательно, с направлением его орта е_=v/v;. Модуль вектора тангенциального ускорения, как следует из рис 3.2, равен w_ = wcos(v,w). Значение cos(v,w) можно найти, используя определение скалярного произведения векторов (2.3): cos(v,w) = .

Таким образом, w_==;

Из определения (3.10) найдем значение w_n = w – w_ =.

Отв. w_ =; w_n = .

Пример 2. Зависимость модуля скорости v от пройденного пути S определяется функцией v(S) = v₀–bS.

Найти зависимость пути S(t) и модуля скорости v(t) от времени t.

Решение

Из определения (3.6) следует dS = vdt = (v₀–bS)dt.

Это дифференциальное уравнение первого порядка можно решить методом разделения переменных: .

Проинтегрировав обечастиэтого уравнения, получим:

.

Зависимость v(t) можно получить, используя полученный результат:.

Отв. .

Пример 3. Из точки А вертикально вверх бросают «тарелочку». В т.В, отстоящей от т.А на расстоянииS стоит спортсмен, стреляющий по «тарелочке». Скорость вылета пули равна v_0п. Под каким углом  должен выстрелить спортсмен, чтобы попасть в «тарелочку», если он стреляет в тот момент, когда «тарелочка» застывает в воздухе на высоте H? Зависит ли угол прицеливания от начальной скорости пули v_0п? На какой высоте h пуля попадет в «тарелочку»? Сопротивление воздуха не учитывать.

Решение.

Без учета сопротивления воздуха движение пули и «тарелочки» можно считать движениями с постоянным ускорением g.

Следовательно, для описания движения пули и «тарелочки» воспользуемся уравнениями (4.5, 4.6).

Выберем систему отсчета, связанную с Землей. Начало отсчета декартовой системы координат с горизонтальной X и вертикальной Y осями совместим с точкой выстрела спортсмена. Начало отсчета времени совпадает с моментом выстрела.

Нанесем на чертеж начальные кинематические параметры пули (r_0п= 0, v_0п, w_п = g) и «тарелочки» (r_0т, v_0т = 0, w_т=g).

Спроектируем векторное уравнение (4.6) для пули и «тарелочки на оси X и Y. Получим:

; ;;.

В момент времени  попадания пули в тарелочку их координаты должны быть равны. Этот момент времени мы можем найти, приравняв их x-координаты: . Приравниваяy-координаты для момента времени , определим угол , под которым должен быть произведен выстрел:

.

Высоту h, на которой пуля попадет в тарелочку, определим, подставив значение  в любое уравнение для координаты y: . Здесь мы использовали тригонометрическое тождество:.

Угол прицеливания  не зависит от скорости пули, но требование h > 0 накладывает ограничения на начальную скорость пули . Если скорость пули будет меньше, то она не долетит до точки бросания «тарелочки».

Отв. ;.