Электромагнитные явления в индукторе
Как было рассмотрено выше, цилиндрический индуктор создает цилиндрические электромагнитные волны, падающие на боковую поверхность металла в тигле, который находится внутри индуктора. При этом сам индуктор представляет собой полый металлический цилиндр, на внутреннюю поверхность которого падают цилиндрические волны собственного электромагнитного поля (см. рис. 81). Поглощение энергии этих волн приводит к потерям мощности в рассматриваемой системе «индуктор – металл».
Поток электромагнитной энергии, которую несет цилиндрическая волна через «активную» внутреннюю поверхность sвт = πDвтhи индуктора высотой hи, также определяют по среднему за период значению векторного произведения 0,5[EψHz*]sвт, т.е. вектору Пойнтинга. Скалярное выражение вектора Пойнтинга позволяет получить формулы для определения:
активной мощности, теряемой в индукторе, кВт:
, (153)
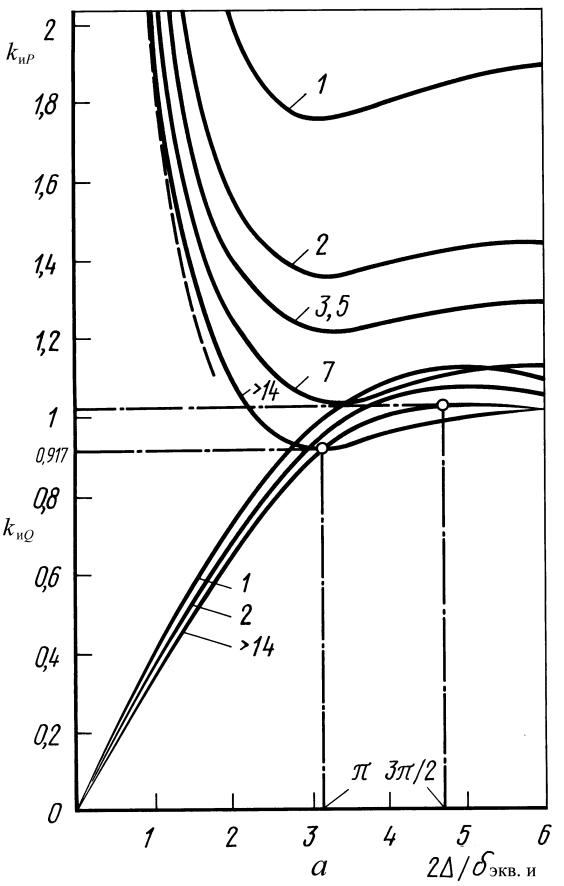
где kиP – коэффициент активной мощности, характеризующий усло- вия затухания цилиндрической волны в индукторе в отли- чие от плоской волны и зависящий от Δ/δэкв.и и Dвт/δэкв.и (рис. 84); остальные обозначения см. в (145) и (148);
реактивной мощности, возникающей в индукторе, квар:
*, (154)
где kиQ – коэффициент реактивной мощности, характеризующий условия затухания цилиндрической волны в индукторе в отличие от плоской волны и зависящий от Δ/δэкв.и и Dвт/δэкв.и (см. рис. 84).
Учитывая физический смысл величины Ри как электрические потери в системе «индуктор − металл» и стремление ее уменьшить при прочих постоянных условиях, индуктор изготовляют из меди марки Ml (ГОСТ 859–2001), имеющей наименьшее УЭС при 293 К ρ293 ~ ~ 1,75∙10–8 Ом∙м, и обязательно охлаждают водой, чтобы температура была не выше 323 К и ρ323 ~ 2∙10–8 Ом∙м. Поскольку медь является диамагнитным материалом (μr ≈ 1), в формулах (153) и (154) значение μr опущено.
Кривые рис. 84, а показывают, что при больших значениях относительного диаметра (Dвт / δэи > 14) минимальное значение коэффициента kиP и, следовательно, электрических потерь в индукторе Ри (при неизменных других величинах) можно достигнуть при условии
. (155)
|
|
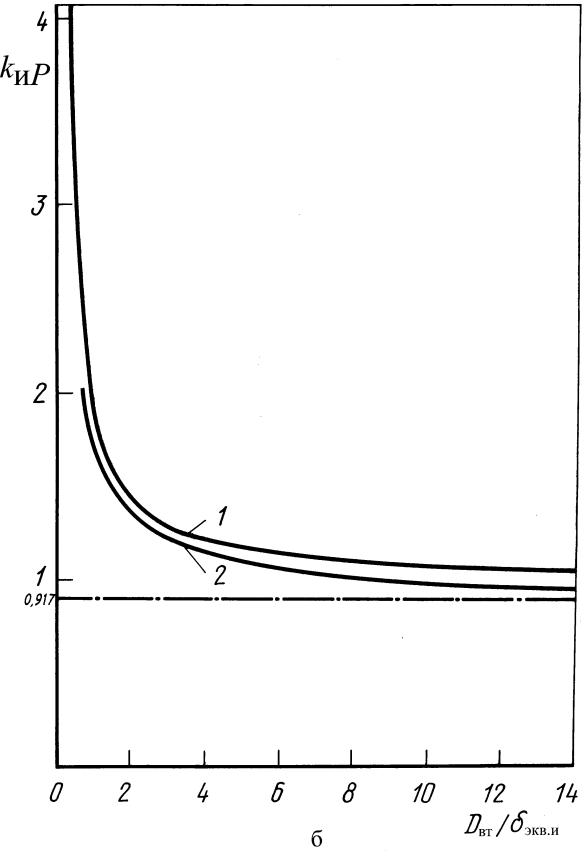
Рис. 84. Кривые для
определения коэффициентов при расчете
потоков активной (kиP)
и реактивной (kиQ)
мощностей, проходящих через внутреннюю
поверхность цилиндрического индуктора:
а – в функции аргумента 2Δ/δэкв.и
для различных значений относительного
диаметра индуктора Dвт/
δэкв.и (числа у кривых); б – в
функции отношения Dвт/
δэкв.и
при относительной
толщине стенки индуктора 2Δ/δэкв.и
(кривая 1)
и 2Δ/δэкв.и =
(кривая 2)
Это выражение широко используют при конструировании деталей индукционных печей при одностороннем воздействии магнитных полей большой напряженности.
Для рассмотрения зависимости kиP от величины относительного «активного» диаметра индуктора на рис. 84, б показаны кривые 1 (для 2Δ/δэкв.и → ∞) и 2 (для 2Δ/δэкв.и = π).
Электромагнитные явления в зазоре
В диэлектрической среде кольцевого зазора между индуктором и цилиндром («металлом») цилиндрическая электромагнитная волна распространяется при отсутствии токов проводимости, при этом в волновых уравнениях независимым переменным является вещественное число βR, где β – коэффициент фазы, показывающий изменение фазы электромагнитной волны [см. формулы (142)] на единичном расстоянии (величина 2π/β представляет собой длину электромагнитной волны).
Поскольку в условиях эксплуатации ИТП аргумент цилиндрических функций очень мал (βR << 0,01...0,001), уравнения электромагнитного поля в зазоре системы «индуктор – металл» (0,5Dм ≤ R ≤ 0,5Dвт) приобретают вид
(156)
Реактивная мощность, возникающая в зазоре и характеризующая скорость превращения энергии электромагнитного поля из электрической формы в магнитную и обратно, равна, квар:
*. (157)