Электромагнитные явления в металлическом цилиндре

Так как математическое выражение решения уравнений через комплексные функции достаточно сложно, дадим графическую интерпретацию уравнений магнитного и электрического полей в сплошном цилиндре в виде зависимости относительного модуля комплексных векторов напряженности магнитного поля

|H_z|_r = |H_z|_R/|H_z|_пврх = χ₁(2R/D_м; D_м/δ_экв.м)

и напряженности электрического поля или, что то же самое, комплексного вектора плотности тока проводимости

|E_ψ|_r = |J_ψ|_r = χ₂(2R/D_м; D_м/ δ_экв.м)

от относительного радиуса сплошного металлического цилиндра R_r = 2R/D_м (рис. 82). При этом следует иметь в виду, что значение R_r = 0 соответствует оси сплошного цилиндра, a R_r = 1 – его поверхности. Для сравнения на рис. 82 в виде штриховой линии нанесены графики относительных модулей векторов для случая падения плоской электромагнитной волны на поверхность массивного проводника при той же частоте, которая соответствует D_м/δ_экв.м = 14. Эти кривые достаточно близки друг к другу, что является основанием применять закономерности распространения плоской волны в полуограниченном теле и для случая индукционного нагрева цилиндрических тел при условии D_м/ δ_экв.м ≥ 14.

Рис. 82. Распределение в металлическом цилиндре относительных величин модулей напряженности электрического |Е|_r и магнитного |Н|_r полей, а также плотности тока проводимости |J|_r; числа у кривых – значения D_м/δ_экв.м; штриховые кривые – экспоненты, построенные для D_м / δ_экв.м = 14

Поток электромагнитной энергии, которую несёт цилиндрическая волна через поверхность s_м = πD_мh_м к оси цилиндра («металла»), также определяют по вектору Пойнтинга. Скалярное выражение этого вектора позволяет получить формулы для определения:

активной мощности, выделяющейся в «металле», кВт:

^, (150)

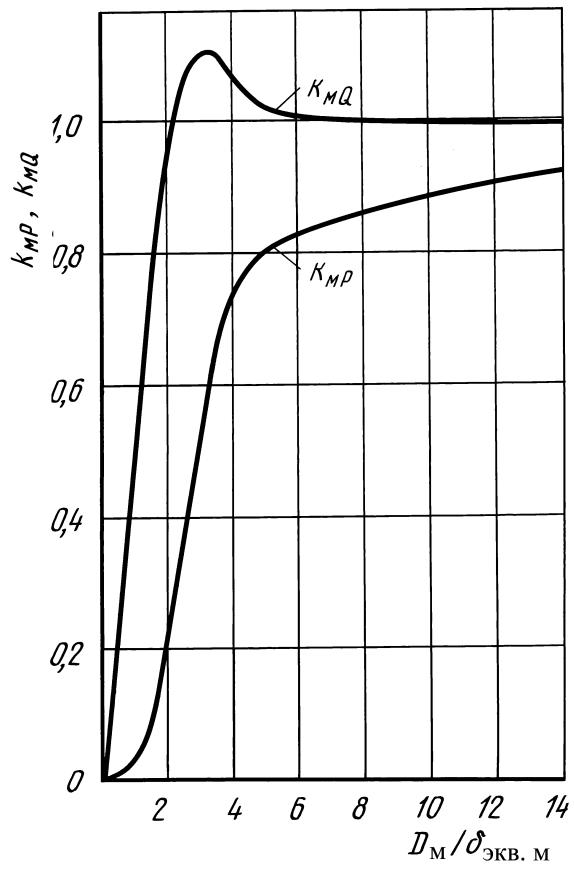
где h_м – высота цилиндра (глубина жидкого металла в тигле), м; k_мP – коэффициент активной мощности, характеризующий усло- вия затухания цилиндрической волны в «металле» (см. рис. 82) в отличие от плоской волны и зависящий от относительного диаметра цилиндра D_м/δ_экв.м (рис. 83);

реактивной мощности, возникающей в «металле», квар:

,^* (151).

где k_мQ − коэффициент реактивной мощности, характеризующий условия затухания цилиндрической волны в «металле» (см. рис. 82) в отличие от плоской волны и зависящий от относительного диаметра цилиндра D_м/δ_экв.м (см. рис. 83).

Рис. 83. Кривые для определения коэффициентов при расчете потоков активной kмР и реактивной kмQ мощностей, проходящих через поверхность металлического цилиндра диаметром Dм

Положение перегиба кривых определяется величиной аргумента æ = D_м/δ_экв.м. В частности, полагая пределом уменьшения относительного диаметра металла значение æ = 10, можно получить формулу для минимально возможной частоты, Гц:

. (152)

Если вместо одного цилиндра диаметром D_м нагревать совокупность N цилиндров диаметром D_ц каждый, при прочих равных условиях можно получить увеличение активной мощности (NР_ц >> Р_м) из-за увеличения «активной» поверхности, когда (NπD_цh_м) >> (πD_мh_м). Однако для ИТП данной вместимости т_о при увеличении числа цилиндров N диаметр каждого цилиндра D_ц, равный , уменьшается, изменяя D_м/δ_экв.м и k_мP (см. рис. 83), в результате чего активная мощность, выделяющаяся в такой «металлошихте», снизится. Таким образом, для данных ρ_м, μ_r и f должен существовать D_ц, обеспечивающий максимальное значение Р_м для ИТП заданных размеров.

Теоретические и экспериментальные исследования Г.И. Бабата показали, что максимум активной мощности, выделяемой в шихте, зависит не только от определенного соотношения между размерами кусков шихты и частотой, но и от самой формы кусков:

цилиндр диаметром D_цл D_цл/δ_экв.м ≈ 3,5;

пластина толщиной Δ Δ/δ_экв.м ≈ 2,5;

немагнитный шар диаметром D_ш D_ш/δ_экв.м ≈ 4,8;

ферромагнитный шар диаметром D_ш D_ш/δ_экв.м ≈ 2μ_r.

У ИТП вследствие разнообразия размеров и неправильной формы кусков шихты оптимальные соотношения приходится подбирать экспериментально для каждой вместимости m_о.