Электромагнитные явления в системе «индуктор – металл»

В течение большей части плавки (с момента, как только расплавится часть шихты, в которой могут разместиться еще нерасплавившиеся куски) шихта представляет собой сплошной цилиндрический блок с μ_r = 1. Сталь удовлетворяет этому условию при температурах выше точки Кюри. Поэтому ИТП можно рассматривать как цилиндрическую систему «индуктор – металл».

Исходными уравнениями для исследования электромагнитных явлений индукционного нагрева в системе «индуктор–металл» являются основные уравнения электромагнитного поля (140) и (141).

Совместное решение уравнений Максвелла, представляющих собой систему уравнений с двумя неизвестными, дает возможность перейти к одному уравнению с одним неизвестным (волновые уравнения):

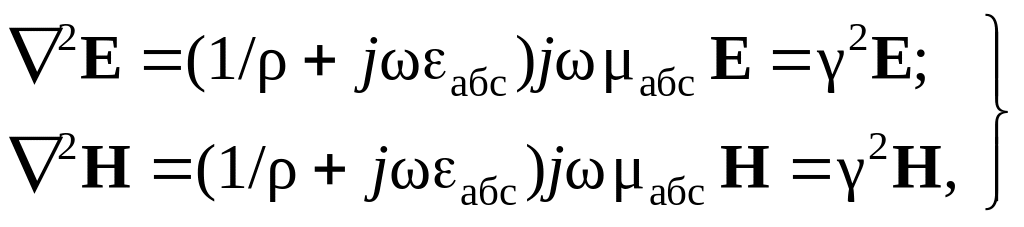(142)

где  – коэффициент распространения, ;  – коэффициент ослабления, ;  – коэффициент фазы, .

Решения волновых уравнений описывают волнообразно распространяющиеся в пространстве процессы изменения величин электрического и магнитного полей, т.е. электромагнитные волны.

Рассмотрим случай падения плоской электромагнитной волны на изотропное полуограниченное металлическое тело с плоской поверхностью; протяженность поверхности нагреваемого объекта и его глубина бесконечны. Напряженность электрического и магнитного полей у поверхности металла обозначим соответственно Е_пврх и Н_пврх, а в металле (на глубине z от поверхности) – Е_z и Н_z. Для нахождения этих величин необходимо волновые уравнения для проводящей среды (142) написать для прямоугольной системы координат. Решение этих уравнений для относительных модулей комплексных векторов имеет вид

(143)

т.е. электромагнитная волна в плоском теле экспоненциально затухает в зависимости от величины коэффициента ослабления α.

Коэффициент α – комплексная величина:

, (144)

где δ_экв – эквивалентная глубина проникновения плоской электромагнитной волны в массивном проводнике, м;

^, (145)

ρ – в Ом∙м; f – в Гц.

Величину δ_экв широко используют в теории индукционного нагрева вообще и при расчетах ИТП в частности.

На расстоянии от поверхности, равном эквивалентной глубине проникновения, амплитуда волны уменьшается в е = 2,71828... раз, т.е. затухает до 36,8 % от своего начального значения (рис. 80, кривая 1).

Электромагнитная волна в проводящей среде сопровождается током проводимости, плотность которого J_z на глубине z может быть найдена по закону Ома:

J_z = E_z/ρ;

J_r = J_z/J_пврх =e^–αz = χ(z / δ_экв). (146)

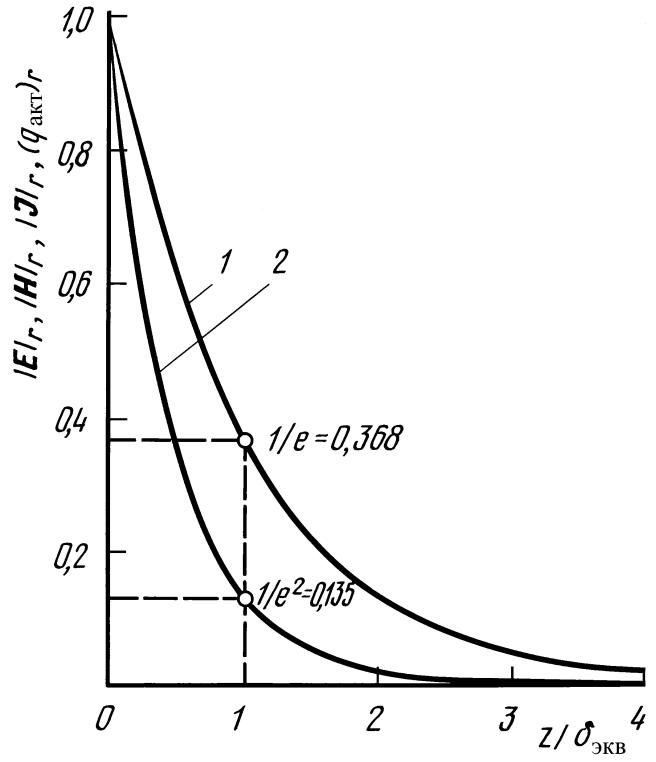
Рис. 80. Изменение относительных величин модуля напряженности электрического |Е|_r и магнитного |В|_r полей и плотности тока проводимости |J|_r (кривая 1), а также плотности потока активной мощности |q_акт|_r (кривая 2) по глубине полуограниченного металлического тела

В ИТП магнитное поле создают, как правило, многовитковыми индукторами. Полагая, что рассматриваемая плоская электромагнитная волна создана соответствующим плоским индуктором с числом проводов N₁ на единицу длины и силой тока в витке I, получим по закону полного тока напряженность магнитного поля у поверхности металла Н_пврх = IN₁ и амплитудное значение

, (147)

где I – действующее значение силы тока в индукторе.

Электромагнитная волна несет энергию, определяемую вектором плотности потока мощности – вектором Пойнтинга^. Величина плотности потока мощности, переносимая плоской электромагнитной волной, убывает по мере проникновения волны в глубь нагреваемого тела по закону (см. рис. 80, кривая 2).

Значение вектора Пойнтинга является комплексной величиной.

Вещественная (англ. Real) часть комплекса, кВт/м²:

^** (148)

определяет плотность потока активной мощности, характеризующую скорость превращения энергии электромагнитного поля в тепловую, а мнимая (англ. Imaginary) часть, квар/м²:

^** (149)

является плотностью потока реактивной мощности, характеризующей скорость превращения энергии электромагнитного поля из электрической формы в магнитную и обратно.

В ИТП электромагнитное поле создают цилиндрические волны (рис. 81): вектор напряженности электрического поля направлен по касательной к окружностям, центры которых лежат на оси цилиндрической волны (Е = Е_ψ; Е_z = 0; Е_R = 0); вектор напряженности магнитного поля направлен параллельно оси цилиндрической волны (Н = Н_z; Н_ψ = 0; Н_R = 0).

Для описания движения такой волны надо вместо уравнений, которые соответствовали плоской волне, составить на основании волновых уравнений (142) аналогичные уравнения в цилиндрических координатах.

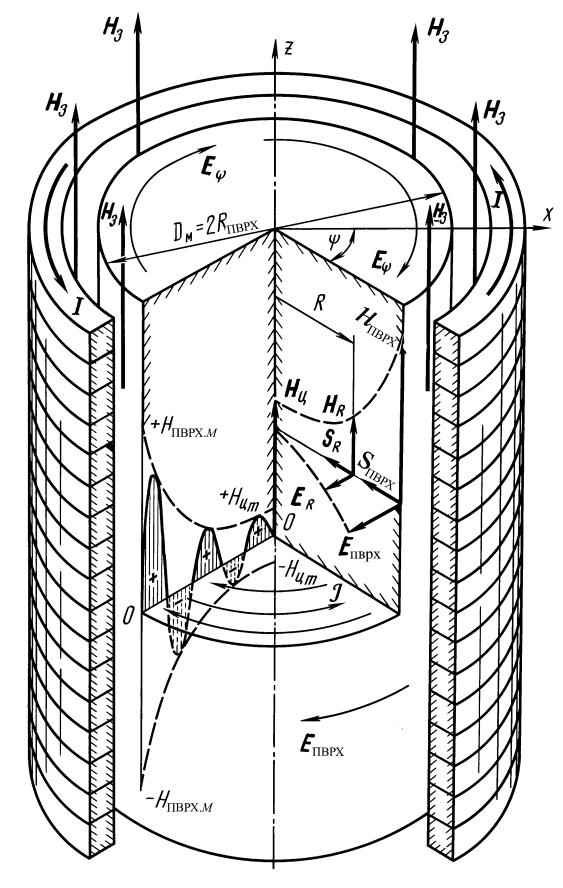
Рис. 81. Падение цилиндрической электромагнитной волны на сплошной металлический цилиндр диаметром D_м: I – ток в индукторе; Н₃, Н_пврх, Н_R и Н_ц – напряженность магнитного поля в зазоре, на поверхности, в точке радиусом R и на оси металлического цилиндра соответственно; ψ – меридианный угол (долгота); на оси O – O показана эпюра мгновенных значений напряженности магнитного поля; стрелки указывают направление соответствующих электрических силовых линий (линии токов проводимости J) по сечению цилиндра