5.3.2 Количественная мера информации

Как показано выше, любой дискретный источник сообщений состоит из наблюдателя и другого источника сообщений (низшего по иерархии). На количественном уровне информацию можно определить как новые знания о состоянии наблюдаемого объекта, а ее количество – как количество нового знания про объект наблюдения. Так как новые знания повышают общий уровень знаний про объект, то количество информации имеет аддитивный характер. С точки зрения наблюдателя неопределенность состояния объекта имеет определенный уровень, пока источник не выбрал новое сообщение. После выбора сообщения источником образуется некоторое количество информации, которое уменьшает эту неопределенность.

Рассмотрение дискретного источника и множества А его сообщений приводит к таким выводам:

1) в сообщении о достоверном событии количество информации равно нулю. Чем больше вероятность сообщения, тем меньше информации оно несет;

2) в двух независимых сообщениях количество информации равно сумме количества информации в каждом из них;

3) количество информаци не зависит от качественного содержания сообщения, т.е. от степени его важности. Это требование обусловлено необходимостью абстрагироваться от содержания сообщения ради достижения общего характера понятия “количество информации”.

Очевидно, общую характеристику количества информации, не связанную с ее содержательным смыслом, дает модель источника – ансамбль сообщений. Если случай достоверный, т.е. его вероятность p(a_i) = p_i = 0 или p_i =1 (случай, который описывается сообщением a_i точно не произойдет или произойдет), то количество информации в сообщении о таком случае I(a_i) = 0, так как уровень неопределенности знаний о состоянии объекта наблюдения после выбора источником такого сообщения не изменяется. Если же источник выбрал не предопределенное заранее сообщение, то уровень неопределенности снизится. Таким образом, количество информации в сообщениях должно быть функцией их вероятности, т.е.

, a_i A, p_i P. (5.2)

Для удовлетворения второго требования необходимо учесть, что вероятность выбора источником двух независимых сообщений a₁ и a₂

, (5.3)

однако суммарное количество информации в них

. (5.4)

Отсюда следует, что функция должна быть такой, чтобы выполнялось равенство

, (5.5)

где , . Кроме того, эта функция должна иметь значения и , если ее аргумент равен 0 или 1. Единственной функцией с такими свойствами является логарифмическая функция

, (5.6)

где k – коэффициент согласования размерности, а основание m логарифма вибирается из соображений удобства. При таком определении количества информации вы-полняются все три требования.

Выбор основания логарифма не имеет принципиального значения, от него зависит только коэффициент k:

,

где .

Учтем, что , и при будем иметь . Чтобы было , выберем k = –1. Тогда

. (5.7)

Обычно принимают m = 2, тогда единицей количества информации будет “бит” (Binary digit). Это количество информации в сообщении о таком случае, который с одинаковой веро-ятностью может произойти и не произойти, т.е. когда моделью источ-ника является ансамбль A = {a₁, a₂), P = {0,5; 0,5}.

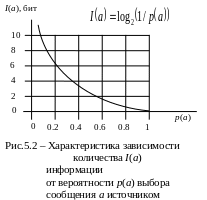
Таким образом, количество информации в сообщении тем больше, чем оно менее вероятно, т.е. более неожиданно (рис. 5.2).