15. Какие прямые и итерационные методы используют для решения систем алгебраических уравнений в задачах с дучп?

К специальным прямым относятся некоторые матричные методы и метод прогонки (аналог метода Гаусса). Из итерационных применяют метод Якоби (одновременных смещений) и метод Гаусса-Зейделя (последовательных смещений), а также модификации последнего, например, метод верхней релаксации.

Рассмотрим один из наиболее простых методов – процесс усреднения Либмана для систем. Согласно методу Либмана вычисления ведутся следующим образом: выбрав начальные приближения , последовательные приближения для внутренних узлов сеточной области , определяем по формулам

,

для уравнения Пуассона и

,

для уравнения Лапласа, которые следуют из конечно-разностных уравнений.

16. Как задаются граничные условия? Каким образом задается начальное приближение при решении дучп с использованием итерационных методов?

Для нахождения единственного решения дифференциального уравнения в частных производных необходимо задать начальные и граничные условия. Начальными условиями принято называть условия, заданные в начальный момент времени tДля эллиптических уравнений задаются только граничные условия, которые можно разделить на три класса:

• условие Дирихле: .

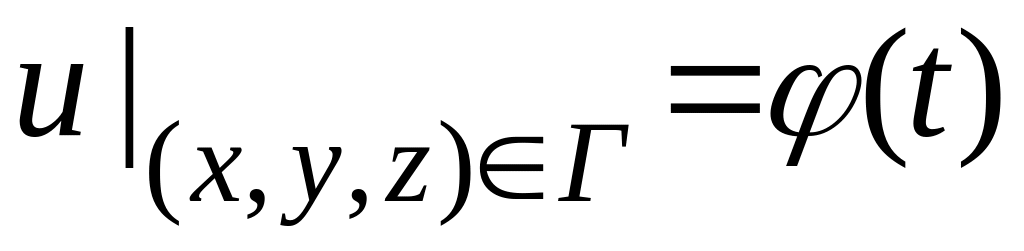В этом случае на границе области Г, в которой ищется решение, задана некоторая непрерывная функция . В одномерном случае это условие принимает вид:

где (0,L) – интервал, на котором ищется решение одномерной задачи;

• условие Неймана: .

В этом случае на границе области задана производная по направлению n внешней нормали;

- смешанное условие: .

Для параболических уравнений, кроме граничных условий, необходимо определить одно начальное, которое может быть таким:

.

В случае гиперболических уравнений начальные условия могут быть следующими:

и

17. Из каких соображений выбирают шаг сетки в методе конечных разностей?

При выборе шага сетки полезно учитывать, что погрешность определяется не учтенными в ней слагаемыми высоких порядков, начиная с (∆x²/12)(∂⁴u/∂x⁴). Поэтому ошибка уменьшается пропорционально квадрату ∆x

Нельзя утверждать, что уменьшение шага сетки однозначно повышает точность решения методом конечных разностей. С увеличением количества узлов сетки возрастает объем вычислений и, следовательно, растут вычислительные погрешности. На практике для оценки погрешности решения можно провести ряд пробных расчетов с разными значениями шага сетки и выбрать вариант, обеспечивающий приемлемую точность при невысоких вычислительных затратах.

18. Каковы источники погрешности при решении задачи с дучп? Каким образом можно оценить погрешность результата численного решения?

Погрешность решения методом конечных разностей в первую очередь определяется ошибкой, вносимой при замене исходного дифференциального уравнения на его конечно-разностный аналог.

Вначале оценим погрешность аппроксимации для первой производной, используя разложение u(x) в окрестностях точки xi в ряд Тейлора:

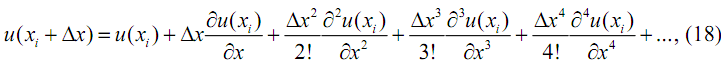
откуда

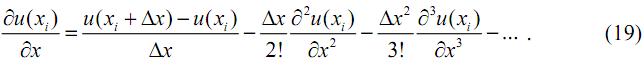
Согласно (18) погрешность конечно-разностной аппроксимация по формуле (6) обусловлена тем, что в ней не учитываются слагаемые высоких порядков, начиная с (∆x/2!)(∂²u/∂x²). Можно утверждать, что в (19) слагаемые убывают по мере увеличения их порядка. Поэтому ошибка (6) приближенно равна (∆x/2)(∂²u/∂x²).

Аналогичную оценку нетрудно провести и для второй производной. Для этого необходимо воспользоваться (18) и аналогичным разложением, записанным для u(xi –∆x):

Сложив (18) и (20) получим выражение для второй производной:

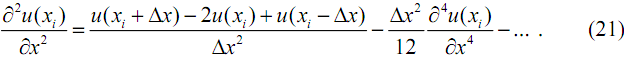
Из сравнения (21) и (8) видно, что погрешность (8) определяется не учтенными в ней слагаемыми высоких порядков, начиная с (∆x²/12)(∂⁴u/∂x⁴). Поэтому ошибка (8) уменьшается пропорционально квадрату ∆x. Данный результат полезно учитывать при выборе шага сетки. Так, например, уменьшение вдвое шага ∆x = ∆y = h приводит к снижению ошибки аппроксимации для уравнения эллиптического типа в четыре раза.