1.3.2. Статистические графики

Графическое представление статистической информации позволяет наглядно отобразить исследуемые явления. В процессе количественного описания различий между группами наблюдений используются многочисленные вычислительные методы, основанные на группировке данных. Графические средства имеют преимущества и позволяют выявить закономерности, которые сложно обнаружить с помощью вычислительных процедур и в процессе количественного описания (например, сложные взаимосвязи, исключения или аномалии). В этих случаях графические методы предоставляют уникальные возможности многомерного аналитического исследования.

Преимущество графического изображения как аналитического метода заключается в возможности с его помощью не только отобразить распределение эмпирических данных, но и определить основную тенденцию изменчивости признака, сгладить его случайные колебания. При наличии современных технических средств безусловным преимуществом графического метода является также простота его применения и скорость получения результатов.

Основные элементы статистического графика. Статистический график представляет собой чертеж, на котором при помощи условных геометрических фигур изображаются статистические данные. В результате этого достигается наглядная характеристика изучаемой статистической совокупности. Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой.

Статистический график включает следующие элементы:

1. Поле графика – место, на котором он выполняется. Поле графика характеризуется его форматом, т. е. его размерами и пропорциями сторон (например, географическая карта, план местности и т. п.). Размер поля графика зависит от его назначения. Стороны статистического графика обычно находятся в определенной пропорции. Принято считать, что наиболее оптимальным для зрительного восприятия является график, выполненный на поле прямоугольной формы с соотношением сторон от 1:1,3 до 1:1,5 (правило "золотого сечения"). Иногда используется и поле графика с равными сторонами (имеющее форму квадрата).

2. Графический образ – геометрические знаки, с помощью которых изображаются статистические данные (точки, линии, прямоугольники, круги, различные объемные фигуры, негеометрические фигуры в виде силуэтов или рисунков предметов и т. д.). Одни и те же статистические данные можно изобразить с помощью различных графических образов. Поэтому при построении графика важен правильный подбор графического образа. Он должен наиболее доходчиво отображать изучаемые показатели и соответствовать основному предназначению графика.

3. Ориентиры:

– пространственные, т. е. определяющие размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значениям изучаемых показателей.

В статистических графиках чаще всего применяются системы прямоугольных декартовых координат. Но могут быть и графики, построенные по принципу полярных координат – круговые графики;

– масштабные – система мер и шкал, принятых для отображения данных.

Масштабной шкалой является линия, отдельные точки которой читаются (в соответствии с принятым масштабом) как определенные числа. Шкала графика может быть прямолинейной и криволинейной (например, окружность). Различают также шкалы равномерные (когда равным графическим интервалам соответствуют равные числовые) и неравномерные (когда равным графическим интервалам соответствуют неравные числовые и наоборот).

И з неравномерных наибольшее распространение имеет логарифмическая шкала. На этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Например, на рис. 1.1 изображена логарифмическая шкала, построенная на основе десятичных логарифмов.

Шкала, на которой указываются уровни изучаемых показателей, как правило, начинается с нуля. Последнее число, наносимое на шкалу, несколько превышает максимальный уровень, отсчет которого проводится по этой шкале. При построении графика допускается разрыв масштабной шкалы. Этот прием используется для изображения статистических данных, имеющих значения лишь в определенных пределах.

4. Экспликация графика – текст, поясняющий его содержание. Экспликация включает название графика, которое в краткой форме передает его содержание, объяснение масштабных шкал, пояснение отдельных элементов графического образа. Цифровые обозначения шкалы дополняются указанием единиц измерения.

Классификация статистических графиков. Существует множество видов графических изображений. Исследователь должен уметь правильно оформлять и анализировать графики. Использование компьютера и соответствующих программ существенно ускоряет работу по созданию графика. Рассмотрим основные виды графиков и наиболее частые случаи их использования.

Статистические графики классифицируются по следующим признакам:

1) способу построения:

– диаграммы – это графики количественных отношений, применяются для наглядного сопоставления в различных аспектах (пространственном, временном и т. д.) независимых друг от друга величин;

– статистические карты – графики количественного распределения по поверхности, представляют собой условные изображения статистических данных на контурных географических картах;

2) форме применяемых графических образов:

– точечные;

– линейные;

– плоскостные;

– объемные;

3) характеру решаемых задач:

– сравнения;

– структуры;

– изменения явления во времени (графики динамики);

– взаимосвязи показателей (факторных и результативных);

– используемые для изображения вариационных рядов.

Рассмотрим три типа графиков, выделенных по характеру решаемых задач: сравнения, структуры и вариационных рядов. (О графиках динамики и взаимосвязи будет подробно рассказано в соответствующих разделах.)

Графики (диаграммы) сравнения

Графики сравнения показывают соотношение признаков статистической совокупности, относящихся к разным объектам, и обеспечивают наглядное сравнение нескольких показателей.

Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы. При их построении используется прямоугольная система координат. При этом каждое значение изучаемого показателя изображается в виде вертикального прямоугольника – столбика, основание которых размещается на оси абсцисс. Количество столбиков определяется числом изучаемых показаний (данных). Расстояние между столбиками и их ширина могут быть произвольными, но обязательно – одинаковыми, у основания дается название изучаемого показателя. Высота столбиков (в соответствии с принятым по оси ординат масштабом) должна строго соответствовать изображаемым данным.

Пример 1.14. Столбиковая диаграмма сравнения изображена на рис. 1.2.

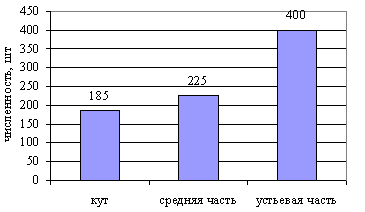
Рис. 1.2. Плотность поселения фукусов (Fucus vesiculosus) на 1 м² на литорали в разных частях одной из губ Кольского залива

Правила построения столбиковых диаграмм допускают расположение на одной горизонтальной оси изображений нескольких показателей группами, для каждой из которых может быть принята разная размерность варьирующих признаков.

Пример 1.15. Диаграмма сравнения групп показателей с разной размерностью варьирующих признаков изображена на рис. 1.3.

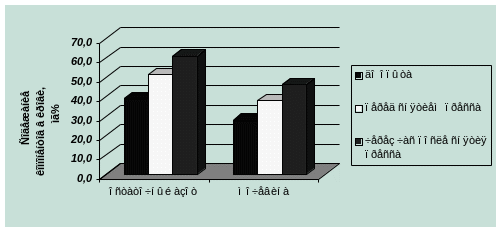
Рис. 1.3. Влияние сдавления на содержание остаточного азота и мочевины в крови

Разновидностью столбиковых диаграмм являются ленточные (полосовые) диаграммы. В этих диаграммах основания столбиков располагаются вертикально.

Пример 1.16. Ленточная диаграмма изображена на рис. 1.4.

Рис. 1.4. Число видов в четырех разновеликих флорах

Графики (диаграммы) структуры

Структурная диаграмма позволяет показать соотношение различных частей статистической совокупности. Состав статистической совокупности графически может быть представлен с помощью как абсолютных, так и относительных показателей. В качестве графического образа для изображения структуры совокупностей применяются прямоугольники (для построения столбиковых и полосовых диаграмм) и круги (для построения секторных диаграмм).

Пример 1.17. Структурная секторная диаграмма изображена на рис. 1.5.

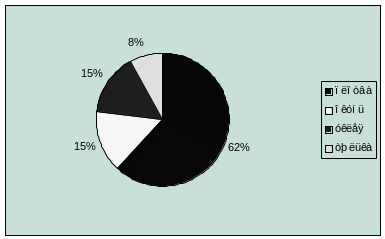
Рис. 1.5. Частота встречаемости видов рыб в пищевом комке щуки

Различные способы графического изображения структуры совокупности имеют преимущества и недостатки. Так, секторная диаграмма сохраняет наглядность и выразительность лишь при небольшом числе частей совокупности, в противном случае ее применение малоэффективно. Кроме того, наглядность секторной диаграммы снижается при незначительных изменениях структуры изображаемых совокупностей: она выше, если имеются существенные различия сравниваемых структур. Преимуществом столбиковых (ленточных) структурных диаграмм по сравнению с секторными является их большая емкость, возможность отразить более широкий объем полезной информации.

Изображения вариационных рядов

Для графического изображения вариационных рядов используются полигон частот (или относительных частот), гистограмма и кумулята (полигон накопленных частот).

Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков имеют координаты (x_i,n_i) (или (x_i,w_i)), где x_i – значение варьирующегося признака; n_i – соответствующая ему частота (w_i – частость, или относительная частота).

Пример 1.18. Полигон частот для вариационного ряда, рассмотренного в примере 1.11, показан на рис. 1.6.

Р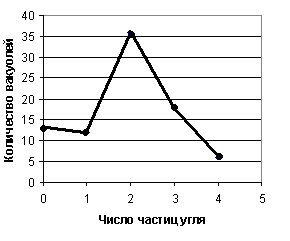 ис. 1.6. Распределение вакуолей парамеций по числу частиц угля

Гистограмма используется для изображения интервальных вариационных рядов. Она представляет собой ступенчатую фигуру, составленную из смежных друг с другом прямоугольников, основания которых равны интервалам значений варьирующегося признака.

Гистограмма может быть преобразована в полигон распределения, если соединить середины верхних оснований прямоугольников прямыми линиями.

Рассмотрим несколько вариантов построения гистограмм:

1. Вариационный ряд с равными интервалами. В этом случае высоты прямоугольников прямо пропорциональны частотам (частостям) n_i (w_i) интервалов. При построении одной гистограммы (или нескольких не связанных между собой гистограмм) по оси ординат можно откладывать частоты и частости. Но если есть необходимость сравнить между собой различные гистограммы (в частности построенные для выборок с различными объемами), то следует откладывать именно частости, так как при этом устраняется влияние объема выборки при сравнении изучаемых распределений.

Пример 1.19. Г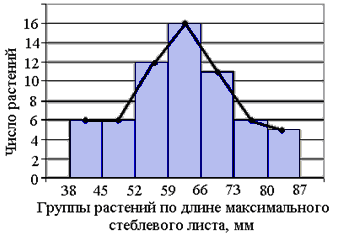 истограмма частот для вариационного ряда, рассмотренного в примере 1.12, изображена на рис. 1.7.

Рис. 1.7. Распределение растений нивяника обыкновенного по длине максимального стеблевого листа

2. Вариационный ряд с открытыми интервалами. В этом случае используется стандартный прием: условно ширина первого открытого интервала принимается равной ширине следующего интервала; ширина последнего принимается равной ширине предыдущего. Таким образом, эта гистограмма будет аналогична гистограмме с равными интервалами.

3. Вариационный ряд с неравными интервалами. В данном случае высота прямоугольников должна быть пропорциональна не частотам, а плотности распределения признака в соответствующих интервалах. Таким образом устраняется влияние величины интервала на распределение. Исследователь имеет возможность сравнить частоты. Плотность распределения признака рассчитывается по формуле n_i/h_i, где n_i – частота интервала; h_i – ширина интервала.

Гистограммы отражают распределение частот значений варьирующегося признака. Проанализировав полученные гистограммы, можно ответить на вопросы: какие значения или диапазоны значений исследуемого признака встречаются наиболее часто? насколько различаются эти значения? является ли распределение симметричным или асимметричным, многомодальным (т. е. имеет две или более вершины) или одномодальным? Гистограммы используются для сравнения наблюдаемых, теоретических и предполагаемых распределений.

По форме распределения признака на гистограмме можно судить о природе исследуемого явления. Например, бимодальное распределение позволяет предположить, что выборка не является однородной, т. е., возможно, смешаны два распределения с далеко отстоящими средними значениями.

Многие статистические методы основываются на определенных предположениях о распределениях анализируемых данных (в частности, при использовании параметрических методов требуется, чтобы изучаемый признак имел нормальное распределение). Гистограммы позволяют проверить, выполняются ли эти предположения (для этого следует наложить на гистограмму соответствующую кривую нормального распределения).

Пример 1.20. Гистограмма и кривая нормального распределения представлены на рис. 1.8.

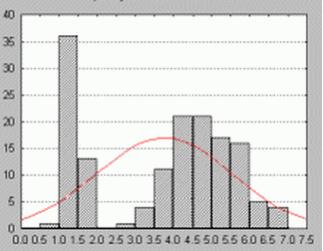
Рис. 1.8. Гистограмма с наложенной на нее нормальной кривой

Для графического изображения вариационных рядов также используют кумуляту (кривую накопленных частот), с помощью которой можно определить структурные средние, проследить за процессом концентрации изучаемого явления.

Кумулята дискретного ряда представляет собой ломаную, соединяющую точки, абсцисса которых равна значению варьирующегося признака x_i, а ордината – соответствующей ему накопленной частотой (частостью). Для интервального ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината – нулю. Абсциссы других точек соответствуют концам интервалов, а их ординаты – накопленным частотам (частостям) соответствующего интервала.

Пример 1.21. К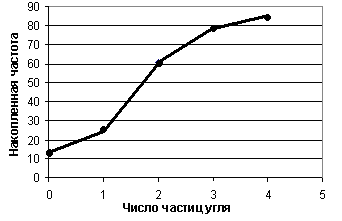 умулята вариационного ряда накопленных частот, представленного в примере 1.13, изображена на рис. 1.9.

Рис. 1.9. Кумулята распределения вакуолей парамеций по числу частиц угля