28. Леса, деревья, остовы. Блоки и точки сочленения

Лес – ациклический граф.

Дерево – связный ациклический граф.

Замечание: Лес является обыкновенным графом.

Теорема: Для (m,n) – графа G следующие условия эквивалентности:

1. граф G – дерево;

2. граф G – связный и m=n-1;

3. G – ациклический граф и число m=n-1;

4. G – граф, в которой любые две вершины соединены единственной простой цепью;

5. G – ациклический граф и добавление нового ребра приводит к появлению ровно одного простого цикла.

Неодноэлементное дерево имеет по крайней мере две висячие вершины.

Лемма: Произвольный (m,n,k)-граф G является лесом тогда и только тогда, когда m=n-k.

Пусть G – связный (m,n) граф, если он содержит хотя бы один цикл, то удаление одного ребра приводит к уменьшению числа циклов по крайней мере на единицу. Таким образом, последовательно разрушая циклы графа, можно прийти к остовному подграфу, являющемуся деревья.

Так как дерево с n-вершинами содержит (n-1)- ребро, то для получения остовного дерева из графа G нужно удалить (m-n+1) ребро. В этом случае мы придем к остовному лесу или остову графа G.

Пр.

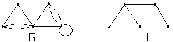Т – остов графа G

Число r*(G)= m - n + k– цикломатическое число графа G (n,m,k).

r(G)=n-k – ранг графа G.

Лемма: Пусть G – произвольный граф. Тогда

1. G ацикличен тогда и только тогда, когда его цикломатическое число r*(G)=0;

2. G содержит единственны цикл тогда и только тогда, когда r*( G)=1.

Лемма: Любой ациклический подграф графа G содержится в некотором его остове.

Блоки и точки сочленения.

Пусть G – произвольный граф.

Вершина V называется точкой сочленения графа G, если граф G-V имеет больше компонентов связностей, чем G.

Неразделимый граф G – связный граф, если он не содержит точек сочленения.

Б лок графа G – любой его максимальный неразделимый подграф.

U и V – точки сочленения.

Лемма: Пусть V-любая вершина связного графа G. Тогда следующие условия эквивалентны:

1. Вершина V- точка сочленения;

2. такие,что V простой (U,W) цепи;

3. разбиение множества вершин графа (G-V) на два непустых подмножества U и W такое, что для любых вершин u U и w W, вершина v простой (U,W) цепи.

Любые две различные блока связного графа G имеет не более одной общей вершины.

Теорема: 1) пусть b₁ и b₂ – два разлиных блока связного графа G, тогда либо они не пересекаются, либо имеют одну общую вершину, которая является точкой сочленения.

2) пусть V – точка сочленения связного графа G , тогда вершина V является общей вершиной по крайней мере двух различных блоков графа G.

3) пусть G – блок, содержащий по крайней мере три вершины, тогда любые две вершины графа G некоторому общему циклу.

Лемма: пусть G-блок, содержащий не менее трех вершин, тогда любая вершина U и любое ребро графа G, не являющееся петлей, некоторому общему циклу.

Теорема: Пусть G – связный граф, содержащий не мене трех вершин, тогда следующие условия эквивалентны:

1. G-блок;

2. Любые две вершины графа G некоторому общему циклу;

3. В графе G любая вершина и любое ребро, не являющееся петлей, некоторому общему циклу;

4. В графе G любые два ребра, не являющееся петлями, некоторому общему циклу;

5. Для любых двух вершин и любого ребра, не являющегося петлей, в графе G существует простая цепь, соединяющая эти вершины и проходящая через данное ребро;

6. Для любых трех вершин U,V,W существует простая (U,W) цепь, проходящая через вершину V;

7. Для любых трех различных вершин U,V,W графа G существует простая (U,W) цепь, не проходящая через вершину V.