22. Сочетания

Сочетанием наз-ся комбинации, составленные из n-элементов по к-элементам, которые различаются хотя бы одним элементом.

Различие между размещением и сочетанием состоит в том, что в размещениях порядок элементов учитывается, а в сочетании – нет.

ПР.: х.у - человек

1. очередь – 2 способа: ху,ух – порядок важен – размещение

2. комиссия – 1 способ - порядок не учитывается – сочетание

ПР.: Сколькими способами читатель может отобрать 3 книги из 4-х:

1) если порядок книг не интересует:

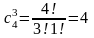
2) если порядок книг интересует:

ПР.: Сколькими способами можно выбрать 2 детали из 10:

ПР.: Сколькими способами можно составить комиссию в составе 3-х человек из 4-х супружеских пар:

1) в комиссию входит любые 3 человека:

2) 2 женщины + 1 мужчина:

Формула связи между размещением, сочетанием и перестановкой.

;

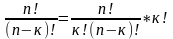
Среди комбинатор. Задач выделяют следующие: пересчет, перечисление, классификация и оптимизация.

Если требуется определить количество элементов, обладающих некоторым свойством или совокупность свойств, то это задача пересчета, если при этом требуется указать список элементов – то это перечисление, если пересчет приводит к очень большим числам, то отказываются от перечисления и классифицируют элементы с помощью какого-либо соотношения. В некоторых задачах можно ввести функцию величины и относительно этой величины рассматривают задачу оптимизации, т.е. найти экстремумы функции на определенном множестве решений.

Комбинаторной конфигурацией называется расположение конечного множества элементов, удовлетворяющих ряду специальных свойств.

Набор элементов (х_i1, x_i2,…,x_ik), составленный из элементов множества х=(x₁,…,x_n) называется выборкой объема к. (n,k выборка)

Если в выборке задан определенный порядок следования элементов, то выборка называется упорядоченной.

Замечание: 2 выборки с различным порядком следования одних и тех же элементов считаются различными.

Выборка, где порядок элементов не существенный называется неупорядоченным.

(n,k) – упорядоченная выборка, элементы которой могут повторяться, называется

размещением из n элементов по к с повторением.

(n,k) – размещение называется перестановкой из n элементов.

Неупорядоченной (n,k) – выборкой называется сочетанием из n элементов по к элементам.

Замечание: Если нет повторяющихся элементов, то . Если есть повторяющиеся элементы, тогда .

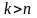Правило суммы в частном случае: Если мощность множества х .

Правило суммы в общем случае: Пусть даны множества х_i, если .

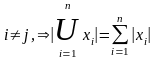24. Элементы теории графов

Графом наз-ся система некоторых объектов с некоторыми парами этих объектов, изображающая отношения связей между ними.

Графы используются для изображения сетей коммуникаций, структурных химических формул, схем, диаграмм, систем бинарных отношений.

Обыкновенным графом называется пара множеств ( ), где , G – обозначение графа, элементы множества - вершины, 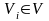, множество всех вершин - 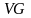, - ребра, , 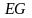- множество всех ребер.

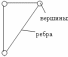
Графом называется тройка (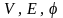 ), где

- отображение множества ,

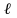- ребро связывает вершины U и V ( )

- означает, что ребро связывает вершину U с самой собой ( ).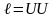

Различные ребра, соединяющие 2 вершины, называются кратными или параллельными:

Ребра с совпадающими концами называются петлями:

В ершина, соединяющаяся ровно с одним ребром и само это ребро называются концевыми или висячими:

То ребро, которое выходит из вершины, называется инцидентным.

Обыкновенным графом называется граф без петель и кратных ребер.

Если граф содержит n-вершин, то он называется n-графом, если кроме того он содержит m ребер, то он называется (n,m) – графом.

Две вершины, инцидентные одному ребру, называются смежными или соседними:

Д ве вершины, инцидентные одному ребру, называются смежными:

Степенью вершины V называется количество ребер, инцидентных данной вершине. Обозначение - , - радиус.

Очевидно, что в обыкновенном графе степень вершины V равна количеству ребер, смежных с V. Петля учитывается дважды.

Окружением вершины V называется количество всех вершин, смежных с ней.

Лемма о рукопожатиях:

Пусть G – Обыкновенный граф, тогда сумма степеней всех вершин равна: (=2 мощностям множества Е)

Если степень вершины V , то вершина V называется изолированной, если - кольцевой:

Граф G называется нулевым, если множество его ребер пусто:

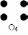
Обыкновенный граф называется полным графом, если любые две его вершины смежные:

К₅

Граф G называется двудольным, если все множество его вершин можно разбить на 2 множества и ребра соединяют только вершины из разных множеств:

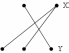
Граф G называется полным двудольным, если все его вершины смежные (из разных доль):

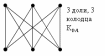
Из леммы о рукопожатиях следует, что степень любой вершины в графе равна:

Количество ребер в двудольном графе: .

Граф H называют подграфом графа G, если

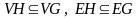
Если множество 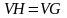, то граф H – остовный подграф.

Редукцией графа G называется такой его остовной подграф H, который является обыкновенным графом с наибольшим и возможным числом ребер.

Граф G называется ориентированным или орграфом, если задана тройка ( ), где 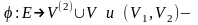упорядоченная пара вершин.

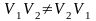если

Граф G называется неориентированным, если задана тройка ( ), где неупорядоченная пара вершин.

В ориентированном графе ребро называется дугой.

Обозначения: