26. Графы и бинарные отношения

Бинарное отношение R – это множество пар a,b декартового произведения множеств M₁ и M₂. ( M₁ – это область определения, M₂ – это область значений, если aRb).

Пусть графу G взаимно однократно соответствует отношение R. G= G(R).

1. Если отношение R рефлексивно, то граф G без кратных ребер, но с петлями во всех вершинах.

2. Если отношение R антирефлексивно, то G без петель и кратных ребер.

3. Если отношение R симметрично, то G неориентированный, без кратных ребер, в котором ребро

4. Если R антисимметрично, то ему соответствует ориентированный граф без кратных ребер, причем исключаются ребра с взаимнопротивоположными ребрами.

5. Если R транзитивно, то в графе G без кратных ребер для каждой пары ребер , замыкающее ребро .

27. Маршруты, цепи, циклы, связность и разрезы

1. G- неориентированный граф.

Маршрут графа G – чередующаяся последовательность вершин и ребер V₀;e₁;V₁;e₂;…;V_t – V₀ V_t – маршрут.

В маршруте вершины и ребра могут повторяться.

Если в маршруте V₀ =V_t, то маршрут замкнутый.

Длина маршрута – это количество содержащихся в нем ребер.

В обыкновенном графе маршрут полностью определяется последовательностью своих вершин.

Частные виды маршрутов:

Цепь – это маршрут без повторяющихся ребер.

Цепь простая(элементарная) – если в ней нет повторяющихся вершин.

Цикл – это замкнутая простая цепь.

Замечание: Петля дает цикл длины 1, пара кратных ребер – цикл длины 2, цикл

длины 3 – треугольники.

Лемма 1: Если для некоторых вершин U и V в графе G существует UV маршрут, то существует и простая UV цепь.

Граф G связный – если любые две его вершины связаны цепью.

Любой граф можно получить как объединение связных графов.

Связность обозначается ~.

Две вершины U и V графа G называются связными, когда существует UV маршрут. U ~ V <=> (U,V) маршрут

Отношение связности является отношением эквивалентности (рефлексивно, симметрично, транзитивно)

Обозначим через V₁, V₂,…, V_n – класс этого отношения и G_i=G(V_i). Тогда графы G₁,G₂,…,G_K называется компонентами связности графа G.

Теорема: Любой граф является дизъюнктным объединением своих компонентов связности.

Обозначается (n, m, k)-граф (где n-количесвто вершин, m-количество ребер, k-количество компонентов связностей).

Разрезающее множество ребер графа – это множество ребер, удаление которого из графа

приводит к увеличению числа компонентов связностей.

Минимальное по включению разрезающее множество графа называется его разрезом.

Мост графа – это ребро , составляющее одноэлементный разрез.

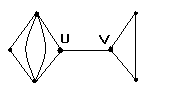
(U,V)-мост

Лемма 2: При удалении из графа моста число его компонентов связностей увеличивается на1.

Лемма 3: При удалении из графа разрезающего множества ребер, число его компонентов

связностей увеличивается на 1.

Для любого графа G есть 2 возможности:

- либо ребро e находится в некотором цикле графа и тогда оно называется циклическим;

- либо ребро e находится ни в одном цикле и тогда оно называется ациклическим.

Лемма 4: Ребро графа является мостом тогда и только тогда, когда оно не содержится ни в

одном цикле.

Лемма 5: Пусть множество вершин связанного графа G разбито на 2 непересекающихся

сомножества U и W. Тогда существует такое ребро e вида (u,v), что u U, а v W.

Теорема: Пусть G – обыкновенный (m,n,k) граф, тогда выполняется двойное неравенство

Следствие: Пусть G –обыкновенный (n,m)-граф, если , то граф G-связный.

2. G- ориентированный граф.

Ориентированный маршрут графа G (ормаршрут) – чередующаяся последовательность его вершин и дуг V₀;f₁;V₁;…f_t-1;V_t либо

Ормаршрут замкнут, если V₀ и V_t совпадают.

Длина ормаршрута – это количество дуг, составляющих ормаршрут.

Орцепь – это ормарашрут, несодержащий повторяющихся дуг.

Орцепь простая – если она не содержит повторяющихся вершин.

Орцикл или орконтур – замкнутая простая орцепь.

Говорят, что вершина V достигаема из вершины U, если существует (U,V)-ормаршрут.

Орграф G сильносвязный (орсвязный) – если любая его вершина достигаема из другой вершины.

Если граф G₀ получается из орграфа G заменой его дуги на ребро , то такой граф G₀ называется основанием графа G.

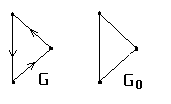
Граф G ориентируемый – если является основанием некоторого сильносвязного орграфа.

Теорема: Связный граф G ориентируем тогда и только тогда, когда каждое каждое его ребро не

является мостом.