24. Элементы теории графов
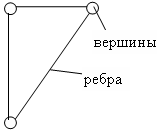
Графом наз-ся система некоторых объектов с некоторыми парами этих объектов, изображающая отношения связей между ними.
Графы используются для изображения сетей коммуникаций, структурных химических формул, схем, диаграмм, систем бинарных отношений.
Обыкновенным графом
называется пара множеств (
),
где
,
G – обозначение графа,
элементы множества
- вершины,
,
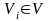множество всех вершин -
,
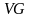- ребра,
,
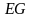- множество всех ребер.
Графом называется
тройка (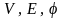
),
где
- отображение множества
,
- ребро
связывает вершины U и V
(
)
- означает, что ребро
связывает вершину U с
самой собой (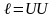
).
Различные ребра, соединяющие 2 вершины, называются кратными или параллельными:
Ребра с совпадающими концами называются
петлями:
В
ершина,
соединяющаяся ровно с одним ребром и
само это ребро называются концевыми
или висячими:
То ребро, которое выходит из вершины, называется инцидентным.
Обыкновенным графом называется граф без петель и кратных ребер.
Если граф содержит n-вершин, то он называется n-графом, если кроме того он содержит m ребер, то он называется (n,m) – графом.
Две вершины, инцидентные одному ребру, называются смежными или соседними:
Д
ве
вершины, инцидентные одному ребру,
называются смежными:
Степенью вершины V
называется количество ребер, инцидентных
данной вершине. Обозначение -
,
- радиус.
Очевидно, что в обыкновенном графе степень вершины V равна количеству ребер, смежных с V. Петля учитывается дважды.
Окружением вершины V называется количество всех вершин, смежных с ней.
Лемма о рукопожатиях:
Пусть G – Обыкновенный
граф, тогда сумма степеней всех вершин
равна:
(=2
мощностям множества Е)
Если степень вершины V
,
то вершина V называется
изолированной, если
- кольцевой:
Граф G называется нулевым, если множество его ребер пусто:
Обыкновенный граф называется полным графом, если любые две его вершины смежные:
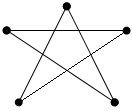
К5
Граф G называется двудольным, если все множество его вершин можно разбить на 2 множества и ребра соединяют только вершины из разных множеств:
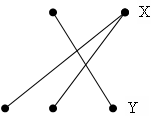
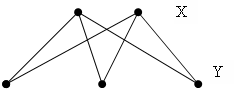
Граф G называется полным двудольным, если все его вершины смежные (из разных доль):
Из леммы о рукопожатиях следует, что
степень любой вершины в графе
равна:
Количество ребер в двудольном графе:
.
Граф H называют подграфом
графа G, если
Если множество
,
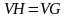то граф H – остовный
подграф.
Редукцией графа G называется такой его остовной подграф H, который является обыкновенным графом с наибольшим и возможным числом ребер.
Граф G называется
ориентированным или орграфом,
если задана тройка (
),
где
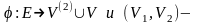упорядоченная
пара вершин.
если
Граф G называется неориентированным, если задана тройка ( ), где неупорядоченная пара вершин.
В ориентированном графе ребро называется дугой.
Обозначения:
25. Способы задания графов
П
еречислением(списком)
всех ребер с отдельным указанием
изолированным списком вершин.
матрица соседства(смежности) вершин
Матрицей смежности называется квадратичная
матрица
,
где
|
U1 |
U2 |
U3 |
U4 |
U1 |
2 |
1 |
1 |
0 |
U2 |
1 |
0 |
1 |
2 |
U3 |
1 |
1 |
0 |
1 |
U4 |
0 |
2 |
1 |
0 |
матрицей инцидентности – это прямоугольная матрица
Неориентированный граф
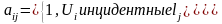
Ориентированный граф
Реализация графа(графическое представление графа).
Графы: плоские и неплоские
В трехмерном пространстве можно реализовать практически любой граф, на плоскости не каждый граф может быть реализован. Граф в трехмерном пространстве на плоскости реализуется при определенных условиях. Тогда вершина обозначается кружочками и тем самым отличаются от пересечения ребер или дуг.
