14. Логические формулы. Булева алгебра

Формулами алгебры логики называются формулы построения из знаков переменных, знаков функциональных операций с соблюдением определенных правил построения формул.

1) 0, 1 – формулы;

2) x, y, z – формулы;

3) - формулы; ( - логические операции)

4) других формул нет.

Законы логики

1)

2)

3)

4)

5)

6)

7)

8)

Дополнительные соотношения:

9)

10)

11)

12)

15. Дизъюнктивные нормальные формулы. Алгебра Жегалкина

Разложение функции f(х₁,…,х_n) по переменной х₁ называется выражение вида

Пример:

СДНФ- есть дизъюнктивная нормальная формула, в которой каждый конъюнкт входит ровно 1 раз, причем либо он сам либо его отражение.

СКНФ- называется конъюнкция некоторых переменных значений, которые равны 0, среди которых нет одинаковых.

ДНФ- дизъюнкция простых конъюнкций.

КНФ- конъюнкция простых дизъюнкций.

Многочлен Жегалкина x₁…x_n от n переменной, называется выражение, состоящее из 0 и 1 обозначения переменной x. Они являются строительным материалом для множества.

Многочлен Жегалкина от n переменной x₁…x_n, называется сумма , где a_j – {0,1} все переменные входят в первую степень, наборы {i₁…i_k}.

Канонический многочлен Жегалкина от n переменных, называется функция вида

20. Любой многочлен Жегалкина может быть приведен к каноническому виду.

Доказательство:

1. Основано на использовании дистрибутивного закона:

2. Правиле приведения подобных:

3. На законе идемпотентности

Т. Любая функция алгебры- логики может быть представлена многочленом Жигалкина.

Доказательство:

Выражение Т. справедливо так как:

Из-за закона Моргана вытекает:

Т. Любая булева функция может быть представлена каноническим многочленом Жегалкина, причем единственное.

Пример: найти канонический полином Жегалкина.

I способ. Равностороннее преобразование.

16. Логика предикатов

Предикат - повествовательное предложение содержащие предметные переменные определенные на соответствующих множествах.

При подстановке этих переменных их значений, предикат превращается в простое высказывание.

Пример: 1) Андрей читает Фрейда.

Михаил читает Фрейда.

--------------------------------

Игорь читает Фрейда.

2) Андрей читает Фрейда.

Михаил читает Михалкова.

---------------------------------

Игорь читает Мольера.

С помощью логических связок предикат может объединяться в предикатные формулы. Исследование предикатных формул и способ установки их истин и есть занятие логики предикатов.

Предикатом Р называется функция отображающая множество Иⁿ во множество В-(0,1), где Р- символ предиката, множество М= -предметная область Р.

Более общее:

Область истинности предикатов. I_p- называется подмножество его предметной области, назначение которой предикат равный 1.

Пример : 1) Р(x;y)={при делении на “3” число х дает остаток у}

-?

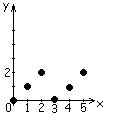Предметной область является множество пар а, b, где

2) R(x,y,z)={при делении на z число х дает остаток у}

3)

a) λ:3x-2y+4z+7=0 L(-3;-5;-2) M(5;13;1) N(7;-4;-9) P=1

L(-3;-5;-2) M(2;6;0) N(7;-4;-9) P=0

Над предикатом на множестве М можно производить логические операции и получать новые предикаты. При этом предметная область нового предиката определяется естественным образом.

Пример: