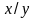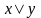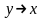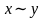12. Основные схемы логических правильных рассуждений
Наряду с алфавитами и правильным построением сложных высказываний в логике высказываний обязательны и правила преобразования логических формул.
Процесс получения новых знаний выраженных высказываниями из уже имеющихся знаний, также выражаются высказываниями, называется рассуждением или умозаключением.
Наиболее употребимые схемы логически правильных рассуждений:
1. Правило заключения – утверждающий
модус:
;
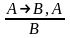2. Правило отрицания – отрицательный
модус:
;
3. Правила утверждения-отрицания:
,
;
4. Правила отрицания-утверждения:
,
,
,
;
5. Правило транзитивности:
;
6. Закон противоречия:
;
7. Правило контрапозиции:
;
8. Правило сложной контрапозиции:
;
9. Правило сечения:
;
10. Правило импортации (объединение
посылок):
;
11. Правило экспортации (разъединение
посылок):
;
12. Правила дилемм: а)
;
б)
;
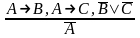в)
;
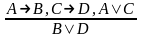г)
.
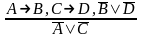13. Алгебра логики
Рассмотрим множество В, состоящее из 0 и1 (В={0,1}). Это бинарное множество элементов которыми являются формальные 0 и 1 не несущими арифметического смысла и интерпретируемые.
Алгеброй логики – алгебра заданная на множестве В вместе со всеми возможными операциями на этом множестве.
Логическими переменными – переменные принимающие значения из множества В. Эти переменные называются булевыми или двоичными.
Функцией алгебра логики или булевой функции f(x1,…xn) называется n-арная логическая операция, то есть f:BnB.
Число всех возможных различных наборов знаний n-переменных логической функции f, равно f=2n.
Чаще всего используются унарные и бинарные логические операции. Унарные операции: P2(1)
x |
0 |
x |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
P2(2):
24=16
x |
y |
0 |
x |
y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Пример:
x |
y |
z |
m3 |
g1 |
g2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
m3 (x,y,z) – наз. функция больш.
g1
(x,y,z)
=
g2 (x,y,z) =
Переменная xk – называется несущественной (фиктивной) переменной функции f(x1, x2,…, xk-1, xk, xk+1,…xn), если f(x1, x2,…, xk-1, 0, xk+1,…xn)= f(x1, x2,…, xk-1, 1, xk+1,…xn) значение.
Если x1 – фиктивная переменная функции f, то первая половина заданного ее столбца значений совпадает со второй. Если отбросить вторую половину этой функции, а затем удалить первый столбец полностью состоящей из 0, то полученная функция f от (n-1) переменных.
Функция которая может быть получена из другой функции удалением или введением фиктивной переменной называется равными.