29. Эйлеровы графы
Эйлерова цепь – замкнутая цепь в графе G, если она содержит все вершины и все ребра графа.
Эйлеров граф – граф, содержит эйлерову цепь.
Эйлеров граф – связный граф, в котором имеется замкнутая цепь, проходящая точно один раз через каждое его ребро.
Теорема: Для неодноэлементного связного графа G следующие условия эквивалентны:
G – эйлеров граф;
Любая вершина графа G имеет четную степень;
Множество всех ребер графа G можно разбить на циклы.
Следствие: Пусть граф G содержит 2l вершин нечетной степени и l ≥1, тогда множество всех ребер графа можно разбить на l цепей, каждая из которых соединяет две вершины нечетной степени.
Полуэйлерова цепь в графе G – если она содержит все вершины и все ребра графа.
Полуэйлерова граф – 1. если в нем существует полуэйлерова цепь;
2. связный граф, в котором имеется цепь, проходящая через каждое ребро ровно один раз.
Утверждение: связный граф G является полуэйлеровым графом тогда и только тогда, когда граф G содержит не более двух вершин нечетной степени.
Следствие: Пусть связный граф G содержит две вершины нечетной степени U и V, тогда
существует (U,V) цепь, содержащая все ребра графа G.
Граф ,произвольновычерчиваемый из вершины V – если любая его цепь с началом в вершине V может быть продолжена до эйлеровой цепи графа G.
Теорема: Неодноэлементный эйлеров граф G является произвольновычерчиваемым из вершины V тогда и только тогда, когда вершина V принадлежит любому циклу графа G.
План построения графа, произвольновычерчиваемого из вершины V:
Возьмем произвольный лес h, любую вершину нечетной степени из h, соединим нечетным число числом кратных ребер с вершиной V, а любую вершину четной степени – четным числом ребер (ø не исключается). Причем любую изолированную вершину из h обязательно соединим с V. Кроме того, к вершине V можно присоединить несколько петель. Получили граф G, который связен, имеет только вершины четной степени, является произвольно вычерчиваемым из вершины V. В таком графе мы можем построить эйлерову цепь: выходим из вершины V и идем произвольным образом по маршруту, соблюдая лишь одно ограничение: из каждой достигнутой вершины только по любому из непройденных ранее ребер, причем движемся до тех пор, пока это будет возможно.
30. Гамильтоновы графы
Гамильтонова цепь графа – его простая цепь, которая проходит через каждую вершину только один раз.
Гамильтонов цикл – цикл графа, проходящего через каждую его вершину точно один раз.
Гамильтонов граф – граф, обладающий гамильтоновым циклом.
Замечание: Вопрос о существовании гамильтоновых цепей и циклов будем рассматривать на основе обыкновенных графов.
Задача поиска гамильтоновых цепей и циклов гораздо сложнее задачи о поиске эйлеровых цепей и циклов и составляет одну из труднейших нерешенных задач теории графов.
Приведем одно из известных достаточных условий существования гамильтоновыхцепей в обыкновенном графе.
Опр. G: V1,V2,…,Vn
Степени вершин: d1,d2,…,dn.
Упорядочены d1≤d2 ≤d3≤…≤dn.
Последовательность d1,d2,…,dn – последовательность степеней графа.
di =deg Vi
Теория Хватала, 1972 г.
Пусть G – обыкновенный граф.
d1≤d2 ≤…≤dn, n≥3.
Если для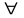
k
верна импликация
,
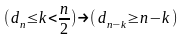то G – гамильтонов граф.
Следствия: 1) теория Дирака,1952 г.
Пусть G – обыкновенный
граф. d1,d2,…,dn,
n≥3. Тогда dk≥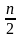
для
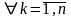
2) теорема Оре, 1960 г.
Deg U + deg V ≥ n для любых двух несмежных вершин графа.
3) dk>k
для
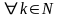1≤k<
Гамильтонова орцепь орграфа – его простая орцепь, которая проходит через каждую его
вершину ровно один раз.
Гамильтонов орцикл – орцикл орграфа, проходящий через каждую его вершину точно один
раз.
Орграф называется полугамильтоновым , если он содержит гамильтонову орцепь и называется гамильтоновым, если содержит орцикл.
Теория Гуйя-Ури: Пусть G – орсвязный n-орграф.
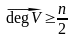и
, то G – гамильтонов орграф.
Турнир – орграф, основанием которого является полный граф.
Теория Редеи и Камион: Любой турнир - полугамильтонов, любой орсвязный турнир – гамильтонов.