1. Основы теории множеств

Кантор – основатель

Множество – набор, группа, количество элементов, обладающих определенными свойствами.

А, В, С,… - множества

x, y, z,… - элементы множества

Важнейшие отношения – это отношения  (принадлежит),  (включает).

х  А

А  В

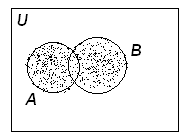 - не строгое включение

Операции над множествами:

1. Объединение – множество элементов х, таких, что х  А или х  В

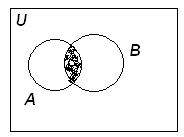
2. Пересечение – множество элементов х таких, что х  А и х  В

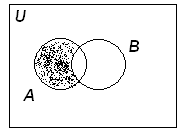
3. Разность – множество элементов х таких, что х  А и х  В

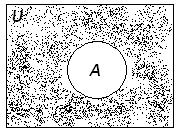
4. Дополнение – множество элементов х таких, что х  U и х  А

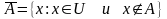
Способы задания множеств:

1. Пересечение элементов:

A = {a, b, c, d}

2. С помощью порождающей процедуры:

(1) 5  М

(2) если а  М, то 1/а  М

(3) если а  М, то (1 – а)  М

Числа Фибаначи:

3. С помощью характеристических свойств:

2. Основные законы теории множеств

1. Закон двойного дополнения:

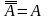
2. Закон коммутативности:

3. Закон ассоциативности:

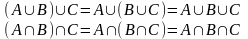
4. Закон дистрибутивности:

5. Закон идемпотентности:

6. Закон Д’Моргана:

7. Законы пустого и универсального множества:

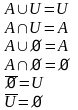
8.

9. Законы поглощения:

Пример:

Доказательство:

1)

Если х  , тогда  х  А или х   х  А или (х  В и х  С) 

(х  А или х  В) и (х  А или х  С)  х 

2) Аналогично образом доказывается в обратную сторону:

3. Декартово произведение множеств. Мощность множества

Декартово произведение множеств А  В называется множество пар элементов а, в таких, что а  А, в  В.

Декартово произведение множеств А₁  А₂  …  А_n называется n-мерный вектор (кортеж) такой, что а₁  А₁, а₂  А₂ …

n раз

Пример: X = {0,1}; Y={a,b}

Найти: XX, XY, YXY?

Решение:

XX = X² = {(0;0);(1;0);(0;1);(1;1)}

XY = {(0;a);(0;b);(1;a);(1;b)}

YXY = {(a;0;a);(b;0;b);(a;1;a);(b;1;b);(a;0;b);(a;1;b)}

Мощность множества называется количество его элементов, содержащихся в множестве.

А

|А|

|A₁A₂A₃…A_n| = |A₁| |A₂| |A₃| … |A_n|

5. Операции над бинарными отношениями

1.

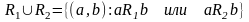
2.

3. Разность: R₁\R₂

4.

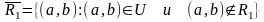
5. Обратное отношение:

6. Композиция отношений:

7. Транзитивное замыкание называется отношение таких, что .

4. Бинарные отношения

Отношение – характеристические связи между элементами множества, между множествами.

Отношения:

• унарные (отношения элементов имеет определенное свойство)

быть желтым (св-во) лимон (эл-т мн-ва) ящик (мн-во)

R a M

a  R, R  M

• бинарные (подмножество пар (а, в), декартово произведение множества)

(а, в)  М₁  М₂ (М₁ – область определения; М₂ – область значений)

aRb

Способы задания бинарных отношений похожи на способы задания множеств: