алгебра

Степенева функція

Функцію , де x — змінна, а p — стале дійсне число, називають степеневою функцією. Властивості степеневої функції залежать від значення p. 1. p Є N. Тоді ; ; Якщо p — непарне, знак y збігається зі знаком x; функція непарна й зростає на всій області визначення. Якщо p — парне, для всіх значень x; функція парна. Якщо , функція спадає, якщо , функція зростає. 2. p Є Z; . Тоді . Графік складається з двох віток; . Якщо p — непарне, то для всіх значень знак функції збігається зі знаком аргументу. Функція непарна, спадна на кожному з проміжків і . Якщо p — парне, для всіх x; функція парна. Якщо , функція спадає, якщо , функція зростає. На рисунках, поданих нижче, наведені графіки степеневої функції для різних значень p:

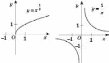
Показникова функція

Функція , де і , називається показниковою (з основою а). Властивості показникової функції : 1. . 1. . 2. . 2. . 3. Функція не є ні парною, ні непарною. 4. Графік функції розміщений у верхній півплощині, перетинає вісь Oу у точці (0; 1), вісь Oх є для нього асимптотою. 5. Функція зростає 5. Функція спа на R. дає на R. 6. Якщо , то . 7. Якщо , то існує, і до того ж єдине, значення x, при якому (Тобто рівняння завжди має розв’язок, і до того ж єдиний, якщо , , .) На рисунку внизу зліва зображений графік показникової функції при ; на рисунку 1 — при . Рис. 1 Рис. 2

Логарифмічна функція

Функцію називають логарифмічною функцією з основою a. Логарифмічна та показникова функції є взаємно оберненими. Властивості логарифмічної функції : Графіки показникової (рисунок 1) і логарифмічної (рисунок 2) функцій з однаковою основою симетричні відносно прямої . Рис. 1 Рис. 2 Радіанна система вимірювання кутів і дуг

1 радіан — це такий центральний кут, для якого довжина відповідної дуги дорівнює довжині радіуса. Формули переходу: від радіанної міри до градусної: ; від градусної до радіанної: , де — градусна міра деякого кута, a — його радіанна міра. Корисно пам’ятати: 2π — 360°, π — 180°, — 90°, — 60°, — 45°, — 30°. Якщо кути виміряні в радіанній мірі, спрощується формула довжини дуги і формула площі сектора , де l — довжина дуги, r — радіус кола, a — радіанна міра центрального кута, S — площа сектора.

Тригонометричні функції числового аргументу

Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці і радіус якого дорівнює 1 (див. рисунок). Нехай точка P0 — це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним — проти. Точку, яку дістанемо поворотом P0 навколо початку координат на кут , назвемо . Очевидно, що значення можуть бути від до , причому кути, міри яких відрізняються на , , дають на колі одну й ту саму точку. Наприклад: , . 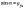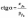Введемо означення: ; ; ; . Значення , , , залежить тільки від кута . Для ці означення дають той самий результат, що й означення за допомогою елементів прямокутного трикутника. Якщо означення , , , уведені таким чином, то очевидно, що ми дістали числові функції. Дійсно, кожному значенню відповідає єдине значення і . Також кожному дійсному значенню , , відповідає єдине значення і кожному значенню , , відповідає єдине значення . Проведемо дотичну t до одиничного кола в точці (див. рисунок нижче). Вона називається лінією тангенсів, тому що ордината точки перетину прямої із прямою t дорівнює тангенсу кута . Проведемо дотичну q до одиничного кола в точці (див. рисунок на с. 73). 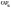Для довільного числа , , абсциса точки перетину прямої з прямою q дорівнює котангенсу кута . Тому пряма q називається лінією котангенсів.