11. Принцип решения прямых и обратных задач магниторазведки, типы магнитных аномалий.

Основные положения теории магниторазведки. При магниторазведке рассчитываются аномалии полного вектора или его составляющих путем исключения из наблюденного поля нормального поля и вариаций. Поэтому в теории магниторазведки определяются эти параметры для объектов с разной интенсивностью и направлением намагничения (J). Для простоты решения можно считать , где k- магнитная восприимчивость объекта, T_ср- средняя напряженность геомагнитного поля в месте его расположения, а остаточной намагниченностью J_t пренебречь.

Основной закон магнетизма был сформулирован Кулоном, который предполагал, что существование магнетизма связано с наличием магнитных масс, положительных и отрицательных. Между двумя магнитными массами m₁ и m₂, помещенными в среду с магнитной проницаемостью 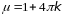действует сила F, которая определяется законом Кулона , где r- расстояние между центрами магнитных масс. Любое намагниченное тело можно представить сочетанием двух таких магнитных масс, находящихся на противоположных частях тела - полюсах. Северным (положительным) полюсом намагниченного тела (например, магнитной стрелки) считается тот, который поворачивается в сторону северного географического полюса, если дать возможность телу свободно вращаться вокруг вертикальной оси. Как отмечалось выше, при таком определении магнитный полюс Земли, находящийся в северном полушарии, обладает южным (отрицательным) магнетизмом, поскольку притягиваются магнитные массы противоположного знака, а массы одного и того же знака отталкиваются.

Прямой задачей магниторазведки называется нахождение магнитных аномалий ( и др.) над объектами известной формы, глубины залегания и намагниченности. Обратной задачей магниторазведки является определение формы, глубины залегания, намагниченности по измеренному площадному распределению аномалий.

Прямая и обратная задачи над вертикально намагниченным шаром.

1 . Прямая задача. Пусть вертикально намагниченный шар с центром на глубине H залегает под началом координат. Необходимо определить напряженность поля вдоль профиля x. Потенциал шара можно представить как потенциал диполя, помещенного в его центре. Поэтому, потенциал шара с магнитным моментом M=JV (или магнитной массой m=M), равен:

Таким образом, в плане над шаром изолинии и будут иметь вид концентрических окружностей. При этом изолинии будут двух знаков, а - одного.

2. Обратная задача. По характерным точкам на графиках можно найти глубину центра вертикально намагниченного шара.

Прямая и обратная задачи над вертикально намагниченным тонким пластом бесконечного простирания и глубины.

Пусть на глубине h параллельно оси y расположен бесконечно длинный вертикальный пласт (с толщиной l, меньшей глубины залегания), намагниченный вертикально. Определим для простоты лишь вдоль оси x.

П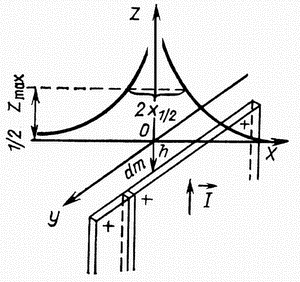 оскольку нижняя часть пласта расположена глубоко, то влияние магнитного полюса глубоких частей пласта будет мало, и можно считать, что магнитные массы сосредоточены вдоль поверхности в виде линейных полюсов. Магнитная масса единицы длины пласта равна

Бесконечно длинный столб

1 . Прямая задача. Пусть на глубине h залегает вершина бесконечно длинного столба (вертикального цилиндра или стержня) сечением s. Его можно представить как тело одного полюса (m) с интенсивностью намагничения (J), направленной вдоль оси z, и "магнитной массой" m=Js. Так как нижний полюс столба расположен очень далеко, то его влиянием можно пренебречь и считать, что вся "масса" сосредоточена на вершине столба.

Н еобходимо найти напряженность поля вдоль профиля x над телом. Потенциал от верхнего полюса столба в точке P будет равен потенциалу точечной массы:

Прямая и обратная задачи для вертикально намагниченного горизонтального цилиндра бесконечного простирания.

Пусть на глубине H параллельно оси y расположен бесконечно длинный цилиндр с магнитным моментом единицы длины, равным M=Js, где J- интенсивность намагничивания, постоянная для всего цилиндра и направленная вертикально, s - поперечное сечение цилиндра. Требуется определить напряженность поля вдоль оси x. Поле такого цилиндра можно считать эквивалентным полю бесконечного числа вертикальных магнитных диполей, центры которых расположены по оси цилиндра.