5.2.1 Структура приложения
Данное приложение состоит из двух модулей, один из реализует интерфейс пользователя(ввод координат), а второй реализует саму программу расчета по алгоритму Монте-Карло. Проект программы состоит из следующих файлов:
Index.html – модуль, содержащий интерфейс взаимодействия с пользователем(GUI). Представляет собой документ html-разметки.
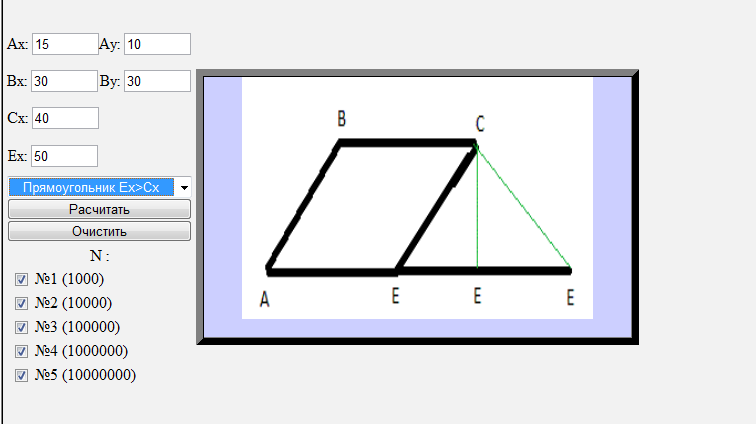
Рисунок 10. Пользовательский интерфейс приложения haXe/PHP
Main.hx – модуль, содержащий функции, реализующие логику программы. При компиляции, на его основе, создаются PHP-файлы.
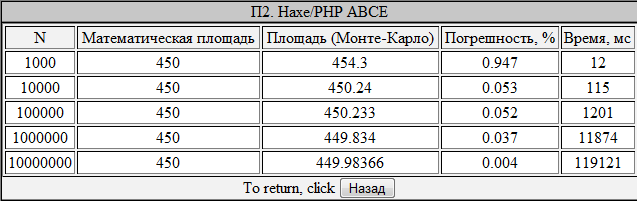
Рисунок 11. Результаты эксперимента haXe/PHP
5.2.2 Проектирование приложения.
Приложение состоит из страницы index.html реализующей пользовательский интерфейс и страницы index.php, которая была автоматически сгенерирована компилятором haXe, и содержит в себе алгоритм расчета площади по методу Монте-Карло. После заполнения пользователем входных данных и нажатия клавиши “Рассчитать”, данные с помощью метода Post передаются на вход скрипту, который производит математические вычисления. После завершения работы, отображается страница с результатами эксперимента.
В процессе создания приложения на языке haxe были спроектированы следующие функции и классы:
Class Main
Static function main() - определяют точку входа в программу.
Static function Math_Square – вычисление площади четырехугольника по правилам геометрии.
static function getCurve - вывод уравнения прямой, для проверки принадлежности точки четырехугольнику(используется в функции MonteKarlo_Square)
static function MonteKarlo_Square – собственно сам метод Монте-Карло. Вначале определяется площадь описанного четырехугольника, затем на основании этого определяется диапазон координат случайных точек, после этого определяется принадлежность точки заданному четырехугольнику. При попадании точки, выполняется увеличение количества точек, попавших в четырехугольник.
В листинге приведено определение попадания точки в четырехугольник:
Листинг №1. Определение попадания точки в четырехугольник. HaXe.
if(x3<x4) //esli c<e(slychai 1)
{
if(randx<x2)
{
newy = getCurve(x1,y1,x2,y2,randx);
if(randy<=newy)
{
points+=1;
}
}
if(randx==x2)
{
points+=1;
}
if(randx==x3)
{
points+=1;
}
if(randx>x2&&randx<x3)
{
points+=1;
}
if(randx>x3)
{
newy= getCurve(x3,y3,x4,y4,randx);
if(randy>=newy)
{
points+=1;
}
}
}
if(x3==x4) //esli c==e(slychai 2)
{
if(randx<x2)
{
newy = getCurve(x1,y1,x2,y2,randx);
if(randy<=newy)
{
points+=1;
}
}
if(randx>=x2&&randx<=x3)
{
points+=1;
}
}
if(x3>x4) //esli c>e(slychai 3)
{
if(randx<x2)
{
newy = getCurve(x1,y1,x2,y2,randx);
if(randy<=newy)
{
points+=1;
}
}
if(randx==x2)
{
points+=1;
}
if(randx==x3)
{
points+=1;
}
if(randx==x4)
{
points+=1;
}
if(randx>x2&&randx<x4)
{
points+=1;
}
if(randx>x4&&randx<x3)
{
newy = getCurve(x3,y3,x4,y4,randx);
if(randy>=newy)
{
points+=1;
}
}