4.2 Логическое проектирование приложения
Настольное приложение испольуюет GUI для взаимодействия с пользователем. Предлагается ввести координаты точек, либо вырбрать контрольный пример. После завершения экспериментов выводится таблица результатов. Схема приложения показана на рис.4
Рис. 4. Схема программы настольного приложения
В процессе создания приложения были спроектированы классы и методы, которые отображены на рис.5
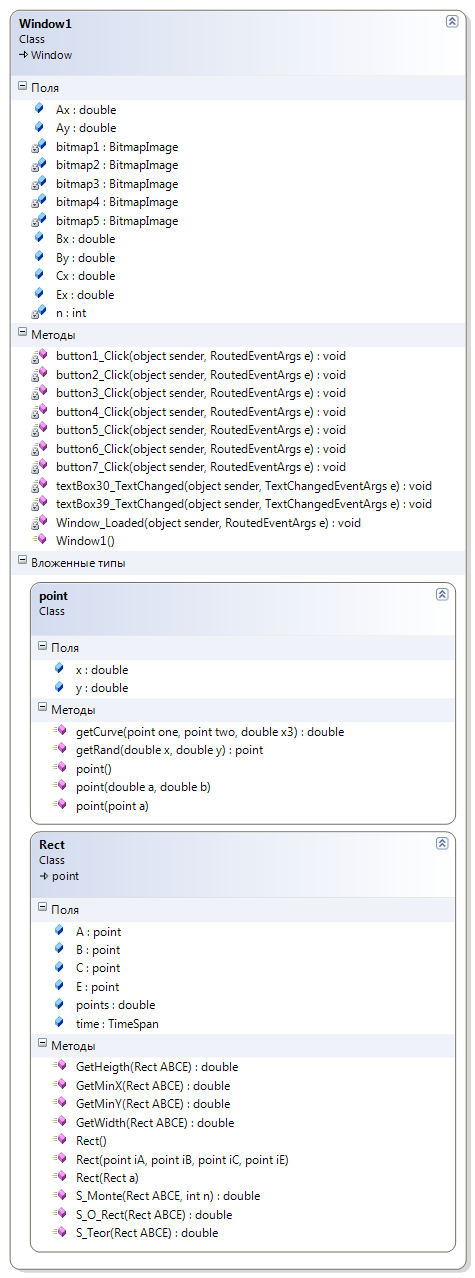
Рис. 5. Структура приложения WPF
В настольном приложении определены следующие классы:
класс точки Point
класс четырехугольника, состоящий из четырех точек Rect
класс окна приложения Window1
В классе Point определены следующие типы данных и методы:
double x, double y – координаты х и у соответствующей точки
конструкторы
get Curve
getRand
В классе Rect определены следующие данные и методы:
point A, point B, point C, point E
double points
TimeSpan time
конструкторы
GetHeigth
GetWidth
GetMinX
GetMinY
S_Monte
S_O_Rect
S_Teor
Cтруктура перечисленных классов, созданная средствами Microsoft Visual Studio, приведена на рис. 6. Пояснения по свойствам методов классов будут даны ниже.
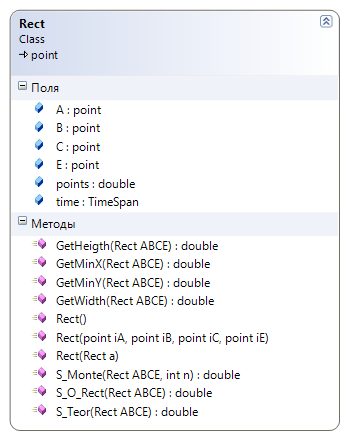
Рис. 6. Классы Point и Rect
Дадим краткие комментарии. Class Window – стандартный класс окна (формы) в приложении WPF. Он генерируется конструктором Visual Studio автоматически, и пересекается с файлом *.xaml, содержащим оформление этого окна. В этом классе определены следующие поля и методы:
private void button_Click(object sender, RoutedEventArgs e) – это обработчики событий, соответствующие нажатию на ту или иную кнопку.
double Ax, Ay, Bx, By, Cx, Ex – в эти переменные записываются введенные пользователем координаты, либо координаты, созданные случайным образом, производится их проверка на корректность и дальнейшее использование классом Point в качестве координат x и у.
int n – количество точек, для которых проводится эксперимент.
BitmapImage bitmap1, bitmap2, bitmap3, bitmap4, bitmap5- содержат 5 изображений, которые используются в настольном приложении в зависимости от того,какой случай четырехугольника будет рассматриваться.
В классе Point определены следующие поля и методы:
double x, y – содержат координаты х и у какой-либо точки
public double getCurve(point one, point two, double x3) – рассчитывает уравнение прямой, для последующего использования в методе MonteCarlo(для определения принадлежности точки заданному четырехугольнику). В качестве аргументов принимает значения 2 точек(A,B или C,E) и координаты х случайной точки.
public point getRand(double x, double y) – Создание новой точки для последующей генерации координат случайной точки в методе Монте-Карло.
В классе Rect определены следующие поля и методы:
point A,B,C,E – Содержат 4 вершины четырехугольника
TimeSpan time – Время проведения эксперимента. Используется тип TimeSpan, так как к этому типу можно применять стандартную функцию для извлечения времени в миллисекундах.
double points – Количество точек, попавших в четырехугольник. При каждом новом эксперименте это значение обнуляется.
public double GetMinX(Rect ABCE)
public double GetMinY(Rect ABCE) – Нахождение минимальных х и у, для расчета ширины и высоты описанного прямоугольника и задания диапазона значений для генератора случайных чисел.
public double S_O_Rect(Rect ABCE) – Нахождение площади описанного четырехугольника.
public double S_Monte(Rect ABCE, int n) – реализует алгоритм расчет площади методом Монте-Карло. Вначале определяется площадь описанного четырехугольника, затем на основании этого определяется диапазон координат случайных точек, после этого определяется принадлежность точки заданному четырехугольнику. При попадании точки, выполняется увеличение количества точек, попавших в четырехугольник. Результаты метода Монте-Карло(количество точек, попавшие точки, площадь Монте-Карло, погрешность, время) записываются в массив типа double, из которого потом в таблицу вносятся результаты.
public double S_Teor(Rect ABCE) - вычисляет площадь прямоугольника ABCE по формулам геометрии.
public double GetHeigth(Rect ABCE)
public double GetWidth(Rect ABCE)- два метода для определения Высоты и ширины описанного четырехугольника