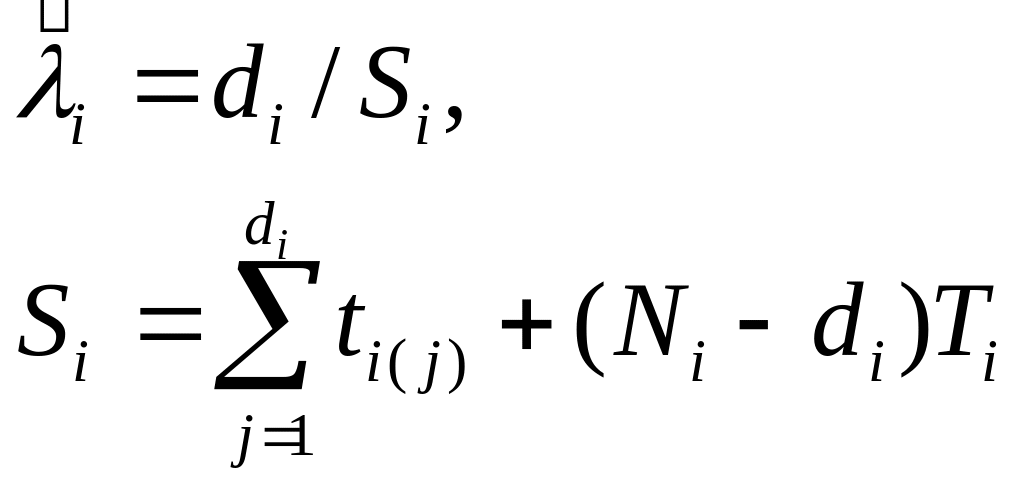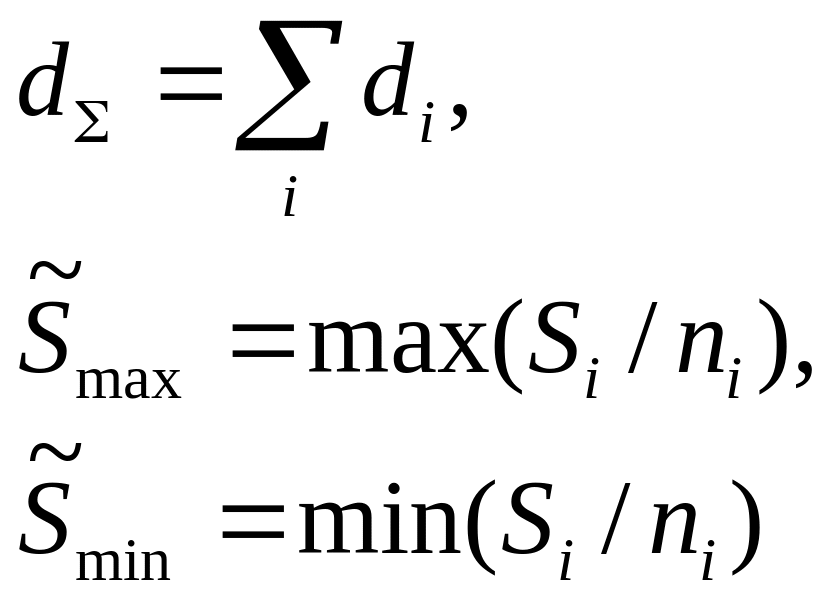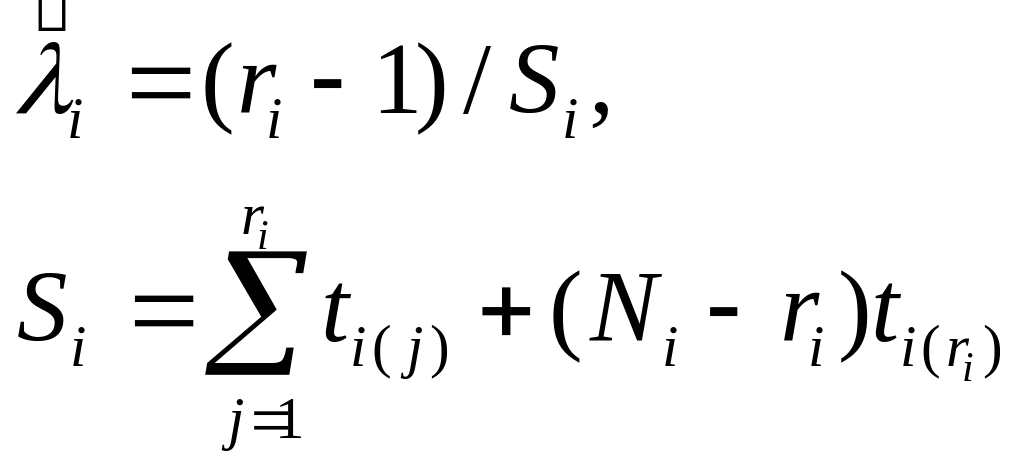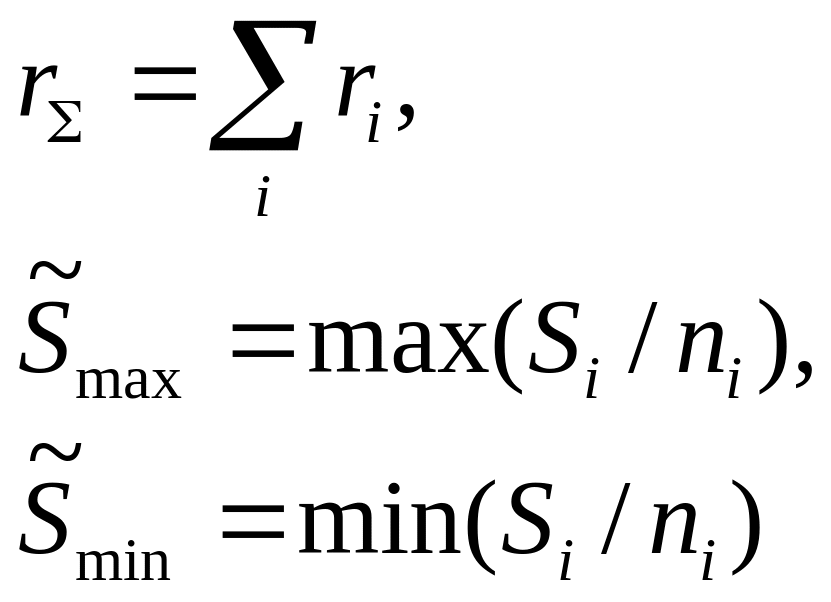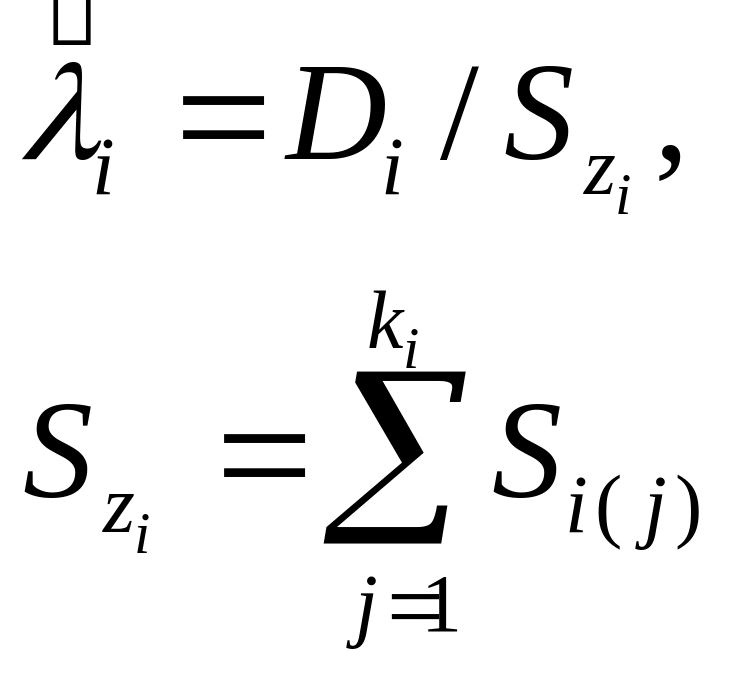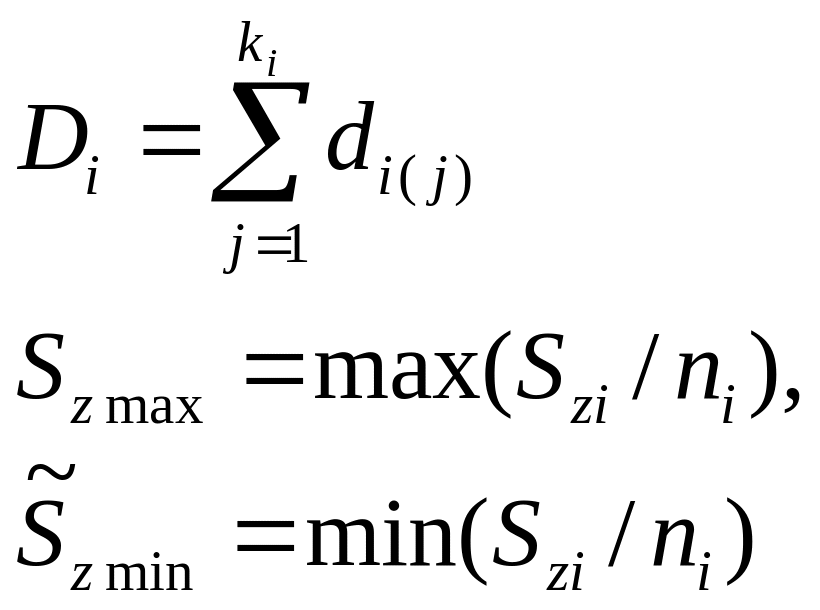БИЛЕТ №29

1. Показатели ремонтопригодности. Способы задания

2. Оценка показателей безотказности и долговечности системы по результатам испытаний элементов

3. Риск, виды риска. Кумулятивный и суммарный риск

1.Показатели ремонтопригодности. Способы задания

Показатели ремонтопригодности

Вероятность восстановления P(t_B) - вероятность того, что время восстановления объекта не превысит заданное:

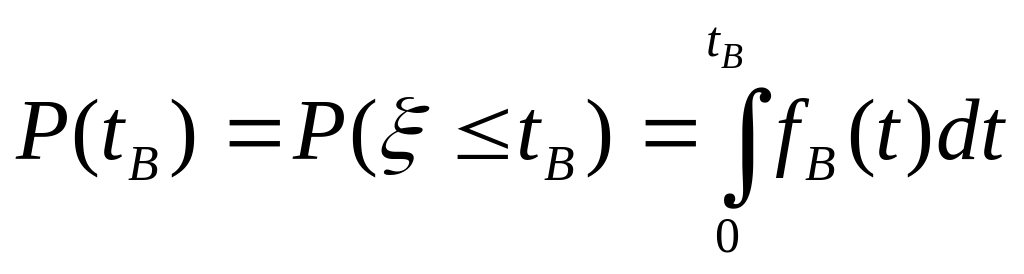, (2.27)

где: f_B(t) - функция плотности распределения случайной величины ξ - времени восстановления работоспособности объекта.

Гамма - процентное время восстановления t_Bγ - время восстановления, достигаемое объектом с заданной вероятностью γ, выраженной в процентах:

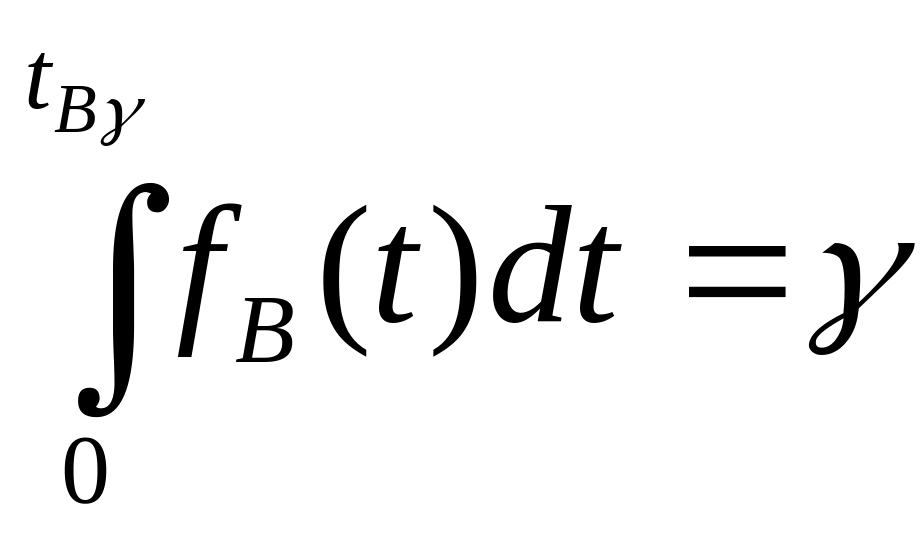. (2.28)

Среднее время восстановления - математическое ожидание времени восстановления работоспособности объекта:

. (2.29)

Интенсивность восстановления μ(t_B) - условная плотность вероятности восстановления работоспособного состояния объекта, определяемая для рассматриваемого момента времени t_B при условии, что до этого момента восстановление не было завершено:

. (2.30)

Средняя трудоёмкость восстановления – математическое ожидание трудоёмкости восстановления объекта после отказа.

2. Оценка показателей безотказности и долговечности системы по результатам испытаний элементов

Оценка показателей безотказности систем с последовательной ссн при планах испытаний с измерением наработки до отказа

В данном случае известны план испытаний и вид закона распределения (или его класс) наработки до отказа i–того элемента. Из всех возможных ситуаций рассмотрим наиболее «определимую», а именно: все элементы испытываются по одному и тому же плану, закон распределения показателей безотказности для всех элементов один и тот же, неизвестны лишь его параметры, есть данные о наработках до отказа или цензурирования каждого из элементов системы.

По этим данным оценивают неизвестные параметры закона распределения наработки до отказа каждого элемента, а затем находят точечные и интервальные оценки вероятности безотказной работы системы с последовательной ССН.

Рассмотрим случай экспоненциального закона распределения наработки до отказа. При этом выберем наиболее простую систему – систему, состоящую из n последовательно соединённых однотипных элементов (типовая ситуация ТС-1). Вероятность безотказной работы такой системы определяется выражением:

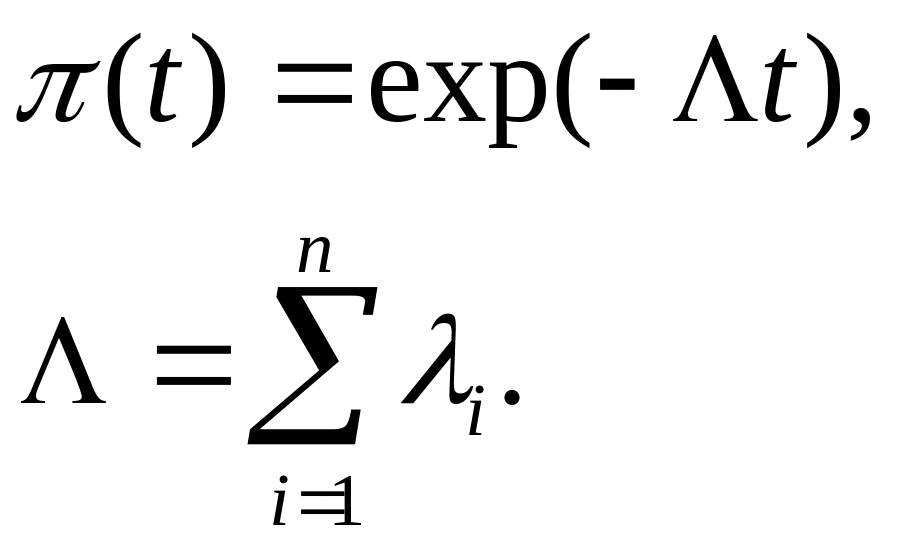
Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям:

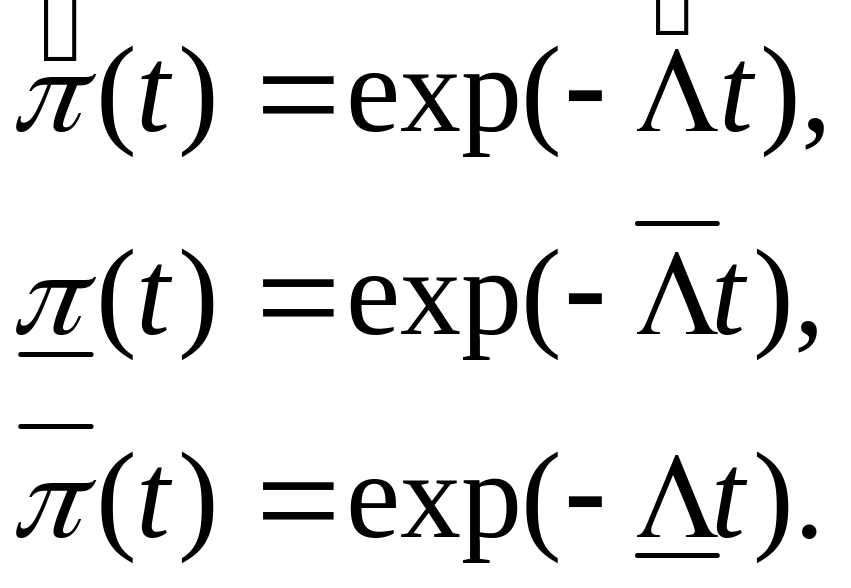
Точечные и интервальные оценки параметра Λ находят по формулам, приведённым в табл. 7.16.

Оценки параметра Λ Таблица 7.16

План испытаний	Точечная оценка	Доверительная граница		Примечание
		нижняя	верхняя
[NiUTi]
[NiUri]
[NiUzi]

Примечание: При одной группе однородных элементов n_i = 1.

Рассмотрим пример простейшей системы:

Оценка показателей долговечности систем с последовательной ССН

Расчёт точечных и интервальных оценок показателей долговечности может производиться по результатам испытаний или эксплуатации объекта.

Для системы, состоящей из m последовательно соединённых элементов, вероятность безотказной работы каждого из которых P_i ,а отказы элементов независимы, показатели долговечности (средний и гамма - процентный ресурс) определяются следующим образом:

Подынтегральное произведение представляет собой вероятность безотказной работы за время t системы из m последовательно соединённых элементов. Т_γ – корень уравнения:

Нижняя доверительная граница гамма – процентного ресурса при доверительной вероятности q есть корень уравнения:

Для распределений с неубывающей интенсивностью отказов (стареющие распределения) оценка снизу определяется при q = 0,5.

Формулы для расчётов показателей долговечности системы по показателям долговечности её элементов для нескольких наиболее простых случаев приведены в табл. 7.17 и 7.18.