Лекция № 6

Поверхности

Геометрические формы отдельных предметов представляют собой сочетание простых геометрических  тел - многогранников и кривых поверхностей.

Многогранники

Многогранник - тело, ограниченное плоскими многоугольниками, называемыми гранями.

 Элементами гранных поверхностей, кроме граней, являются:

Ребра - линии пересечения смежных граней

Вершину - точки пересечения ребер.

Построение проекций многогранника сводится к построению его точек и линий, на чертеже многогранники изображаются проекциями своих вершин и ребер, при этом невидимые линии изображаются штриховыми линиями.

Кривые  линии и их проекции

Кривая - совокупность последовательных положений точки, перемещающейся в пространстве. Кривые делятся на плоские, все точки которых лежат в одной плоскости (окружность, эллипс, парабола) и пространственные (винтовые), на закономерные, которые могут быть выражены аналитически, и случайные, которые задаются только графически. Винтовая линия - линия, описываемая точкой при равномерном движении по прямой, если эта прямая равномерно вращается вокруг параллельной ей оси. Для построения проекций кривой необходимо найти    проекции ряда точек, принадлежащих этой кривой.

Свойства проекций кривых.

1.      Если точка лежит на кривой, то ее проекции лежат на одноименных проекциях этой кривой на одной линии связи.

2.      Плоская кривая, лежащая в проецирующей плоскости, проецируется в прямую.

Образование и классификация поверхностей.

Кривая поверхность - совокупность всех последовательных положений некоторой линии, движущейся в пространстве по определенному закону.

Способы образования поверхностей самые различные, причем одна и та же поверхность может быть получена движением линий разного вида.

Например, боковая поверхность кругового цилиндра:

 а) вращением прямой линии вокруг параллельной ей неподвижной оси,

б) вращением кривой,

в) в результате поступательного движения окружности, центр которой перемещается по прямой перпендикулярной плоскости окружности.

Линия, посредством  которой получена поверхность, называется образующей. Линия, из которой перемещается образующая, называется направляющей.

В зависимости  от вида образующих поверхности подразделяются на линейные ( образующие - прямые) и нелинейные (образующие - кривые)

Линейные поверхности

Цилиндрическая поверхность образована движением образующей, параллельной самой себе, по некоторой кривой. Определена, если задана направляющая по форме и положению и образующая по положению, может быть замкнутой. Тело, ограниченное цилиндрической замкнутой поверхностью и двумя параллельными плоскостями, называют цилиндром. Цилиндр называют круговым, если в его основании лежит круг.

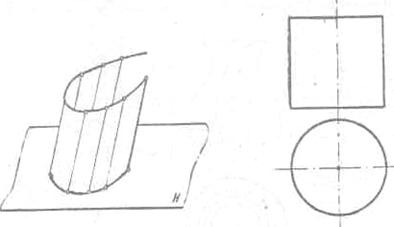
Рис. 32

Коническая поверхность образуется движением прямой линии, проходящей через некоторую точку    (вершину) по некоторой кривой Имеет две полости, определена ни чертеже, если заданы направляющая (по форме и положению) и вершина. Коническая поверхность может быть замкнутой. Тело, ограниченное конической поверхностью, называется конусом. Конус называют круглым, если в основана лежит круг. (Рис.33)

 

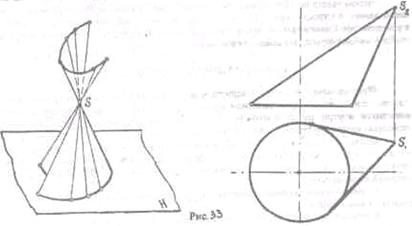
Поверхность вращения определяется на чертеже заданием образующей и оси вращения. Каждая точка образующей описывает при своем вращении окружность с центром на оси. Эти окружности называют параллелями, Наибольшая параллель называется экватором, наименьшая - горлом,

Кривые, получающиеся в сечении тел вращения плоскостями, проходящими через ось (Вращения, называют меридианами. Меридиан, параллельный фронтальной плоскости проекций называют главным ( Рис.34)

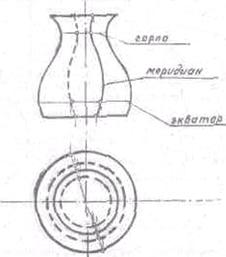
Рис. 34

Построение проекций точек, лежащих на поверхности геометрических тел

Чтобы задать на чертеже проекции точек, принадлежащих геометрическому телу, необходимо построить какую-нибудь линию на заданной поверхности, а затем на проекции этой линии взять проекции искомых точек. В качестве таких линий могут быть выбраны образующие, параллели, меридианы.

Пересечение поверхности плоскостью

 

При  пересечении любого предмете плоскостью получается некая плоская фигура. называется сечением. Под сечением понимают ту часть секущей плоскости, которая

находится внутри рассеченного тела и ограничена линией сечения. Плоскости, с помощью которых получают сечение, называют секущими.

Фигура сечения многогранника - многоугольник, число сторон которого равно числу граней, пересекаемых плоскостью. Вершинами, этого многоугольника являются точки пересечения ребер секущей плоскостью, а сторонами - линии пересечения граней с секущей плоскостью.

В пересечении кривой поверхности плоскостью в общем случае получается плоская кривая линия.

В сечении цилиндрической поверхности могут быть получены:

1.         окружность, если секущая плоскость перпендикулярна оси вращения;

2. эллипс, если секущая плоскость не перпендикулярна и не параллельна оси вращения;

3. две образующие прямые, если секущая плоскость параллельна оси вращения. (Рис.35)

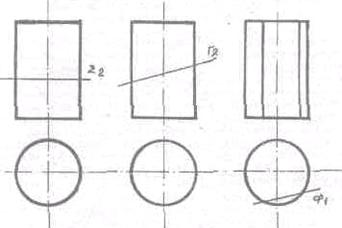
Рис. 35

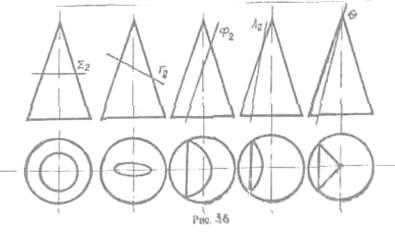
В сечении конической поверхности вращения плоскостью могут быть получены:

1. окружность, если секущая плоскость перпендикулярна оси вращения;

2. эллипс, если секущая плоскость пересекает все образующие поверхности;

3. парабола, если секущая плоскость параллельна только одной образующей поверхности;

4. гипербола, если секущая плоскость параллельна двум образующим поверхности;

5. две прямые, если секущая плоскость проходит через вершину поверхности. (Рмг.36)

При пересечении сферы плоскостью всегда получается окружность.

 

Построение проекций линии сечения поверхности плоскостью общего положения

Для нахождения линии сечения поверхности плоскостью следует в общем случае строить точки пересечения образующих секущей плоскостью, те находить точку пересечения прямой и плоскости. Искомая кривая проходит через эти точки. Эта задача решается легко, если секущая плоскость занимает частное положение. Пользуясь способом преобразования чертежа можно получить удобные для построений положения фигуры, если они Заданы в общем положении в системе П₁П₂. Рассмотрим случай, когда секущая плоскость является фронтально-проецирующей. Так как в данном случае фронтально-проецирующая плоскость пересекает все образующие конуса, то в сечении получится эллипс. Фронтальная проекция эллипса будет отрезком А₂В₂, а горизонтальная проекция будет эллипсом. Построить линию пресечения конуса плоскостью можно при помощи случайных точек. В этом случае их проекции можно находить, используя параллели или образующие конуса. (Рис. 37)

Рис. 37

Рассмотрим случаи пересечения конуса плоскостью общего положения. Этот случаи легко сводится к предыдущему при помощи замены плоскости проекций П₂ на плоскость П₄, перпендикулярную к горизонтали секущей плоскости. Тогда в новой системе плоскостей секущая плоскость будет проецирующей.