41.8. Протокол skip управления криптоключами

Протокол SKIP (Simple Key management for Internet Protocol) может использоваться в качестве интегрирующей среды и системы управления криптоключами.

Протокол SKIP базируется на криптографии открытых ключей Диффи–Хеллмана и обладает рядом достоинств:

• обеспечивает высокую степень защиты информации;

• обеспечивает быструю смену ключей;

• поддерживает групповые рассылки защищенных сообщений;

• допускает модульную замену систем шифрования;

• вносит минимальную избыточность.

Концепция SKIP-протокола основана на организации множества двухточечных обменов (по алгоритму Диффи–Хеллмана) в компьютерной сети.

• Узел I имеет секретный ключ i (i = k_I) и сертифицированный открытый ключ gⁱ mod N.

• Подпись сертификата открытого ключа производится при помощи надежного алгоритма (ГОСТ, DSA и др.). Открытые ключи свободно распространяются центром распределения ключей из общей базы данных.

• Для каждой пары узлов I, J вычисляется совместно используемый секрет (типичная длина 1024 бита): g^ij mod N.

• Разделяемый ключ К_ij вычисляется из этого секрета путем уменьшения его до согласованной в рамках протокола длины 64 -128 бит.

• Узел вычисляет ключ К_ij (используемый как ключ шифрования ключей) для относительно длительного применения и размещает его в защищенной памяти.

Следует отметить, что если сеть содержит n узлов, то в каждом узле должно храниться (n –1) ключей, используемых исключительно для организации связи с соответствующими узлами. Поэтому всего в сети с n узлами должно храниться n∙(n –1)/2 различных ключей и они должны меняться время от времени (срок службы таких ключей составляет недели). Например, при n = 6 число обменов ключей составляет 6∙(6–1)/2=15; при n=1000 число обменов ключей составит 1000∙(1000–1)/2  500000. Поэтому существует практическое ограничение на значение n.

Г лава 42.

Криптографические протоколы на эллиптических кривых

42.1. Основные понятия конечных полей

Кольцо называется полем, если каждый ненулевой элемент обратим и мультипликативная группа кольца абелева. Поле как множество обычно обозначают через F трактуется его как множество замкнутое относительно двух бинарных операций называемых сложением + и умножением∙. При этом пара (F,+) является абелевой группой с нейтральным элементом 0, а пара (F\0, ∙) также является абелевой группой с нейтральным элементом 1. Операция умножения дистрибутивна относительно сложения +. Если множество конечно, то поле F называют конечным и его обозначают через F_q, |F|=q. Множество F\0 (F без нуля) обозначают через F* и называют мультипликативной группой поля F. Для a F обозначим через n a сумму, состоящую из n элементов a. Так как q порядок группы (F_q,+), то q a=0 для любого элемента a F_q (следует из теоремы Лагранжа, в частности q 1=0).

Если для некоторого натурального числа m выполняется m 1=0, то наименьшее из таких чисел называют характеристикой поля F. Если же для любого натурального числа m выполняется неравенство m 1 0, то характеристикой поля называют число 0.

Приведем некоторые основные определения и утверждения.

• Если F – подполе поля H, то характеристики полей F и H совпадают.

• Поле F называется простым, если оно не имеет собственных подполей.

• Если поле не является характеристики 0, то его характеристика есть простое число p.

• Любое конечное простое поле F_p изоморфно кольцу Z/p вычетов целых чисел по модулю p.

• Любое конечное поле F характеристики p содержит простое подполе из p элементов и является его конечным расширением.

• Число элементов q конечного поля F_q равно q=pⁿ, где p характеристика поля F_q.

• Для любого натурального числа n в поле характеристики p выполняются равенства

• Если q=pn, где p – простое число, то поле разложения H над полем Fp многочлена xq-x есть конечное поле из q элементов.

• Мультипликативная группа конечного поля циклична.

Группа точек эллиптической кривой. Пусть конечное поле, характеристики p 2. Рассмотрим многочлен вида

,

. Обозначим через множество корней многочлена Е в поле вместе с бесконечной точкой . Таким образом,

.

Очевидно, что если , то . Мы покажем, что на (в частности, на ) можно ввести групповую операцию. Дадим ряд определений.

1. Пусть К произвольное поле и многочлен от двух переменных над К. Этот многочлен определяет аффинную алгебраическую кривую, которая также обозначается через F:

.

2. Точка называется не особенной, или гладкой на F, если значения частных производных и не равны нулю одновременно. В противном случае точка называется особой. Нетрудно доказать, что все точки , y 0 не особенные тогда и только тогда, когда многочлен не имеет кратных корней. (Кратные точки вида (x,0) вполне возможны, тогда -(x,0)=(x,0). См., например, [Н.Коблиц Курс теории чисел и криптография. М.: ТВП 2001].

3. Пусть – алгебраическое замыкание поля . Пусть также

.

Кривая называется эллиптической, если многочлен не имеет кратных корней. По задаче 1 это эквивалентно тому, что все аффинные точки являются простыми.

4. Вернемся к случаю аффинной кривой F над полем К. Пусть простая точка. Касательной к F в точке Р называется прямая

.

Очевидно, что касательная определена только для неообенной точки Р. В алгебраической геометрии это определение обобщается, и касательная к кривой определяется для любой точки.

ЛЕММА. Пусть и не обязательно различные точки на . Пусть при этом , если и , если . Обозначим через , прямую, которая проходит через , если , и касательную к Е в точке в противном случае. Тогда прямая пересекает ровно в одной точке , координаты которой определяются следующим образом

,

.

ДОКАЗАТЕЛЬСТВО. Пусть и . Тогда прямая, проходящая через , задается уравнением

,

где

, .

Пусть и . Тогда касательная к Е в точке задается уравнением , где

,

так как . Таким образом, для определения надо решить систему уравнений

.

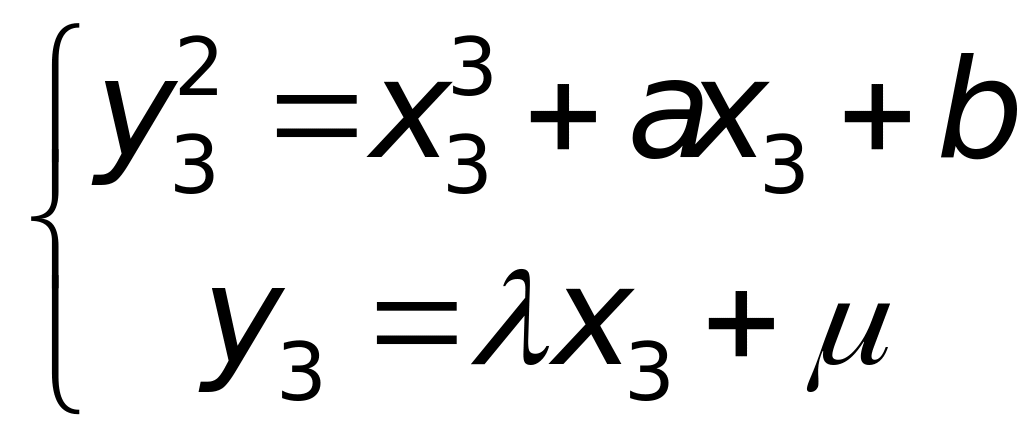После замены имеем . Следовательно, x₃ является корнем многочлена . Этот кубический многочлен имеет 3 корня с учетом кратностей.

Пусть и . Тогда – различные корни этого многочлена. Третий корень можно найти из соотношения (по теореме Виета). Значит, в данном случае лемма доказана.

Пусть теперь и . Покажем, что x₁ – кратный корень r(x). Вычислим для этого . Поэтому

.

Значит, (по теореме Виета), и в данном случае лемма доказана.

Пусть теперь , но . Точки определяют вертикальную прямую . Положим по определению, что  есть третья точка пересечения данной прямой и . Очевидно, что других точек пересечения прямой и нет. Аналогично, если и , то прямая есть касательная к Е в точке P₁. Здесь также полагаем, что  есть третья точка пересечения вертикальной касательной и . Если даны точки и , то третья точка пересечения вертикальной прямой и кривой есть точка . При имеем . Если , то полагаем, что третей точкой пересечения касательной в точке и кривой является .

Из доказанной леммы и приведенных рассуждений видно, что произвольные, не обязательно различные точки кривой однозначно определяют третью точку на . Этот замечательный факт позволяет определить операцию на . Положим . Пусть произвольные точки на . Положим , где R третья точка пересечения с прямой, проходящей через . Очевидно, что однозначно определена. Легко доказать, что множество замкнуто относительно , операция  коммутативна, точка  является нейтральным элементом и каждая точка имеет обратный, то есть существует со свойством . С учетом этого для доказательства того, что есть абелева группа, достаточно показать ассоциативность операции . Но этот факт сложен для доказательства (см. [Fulton W. Algebraic curves: Introduction to algebraic geometry, NY, Benjamin, 1969]).

Для удобства выпишем формулы определяющие . Имеем для всех и , если и . Во всех остальных случаях , , где

,

,

, при ,

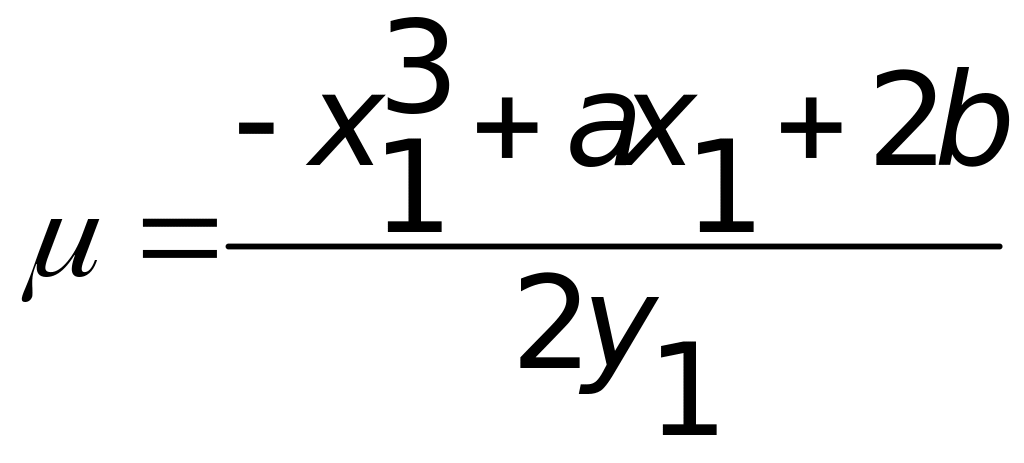, при , .

ПРИМЕР. Определим элементы группы для эллиптической кривой . Для этого составим таблицу

X	0	1	2	3	4	5	-1	-2	-3	-4	-5
X2	0	1	4	9	5	3	1	4	9	5	3
	1	3	0	9	3	-1	-1	-9	-7	-1	3
Y	1	5	0	3	5	-	-	-	2	-	5

Таким образом, . В входят точки

.

Вычислим степени точки (0,1). Имеем . Действительно, и . Тогда

и .

Далее ,

,

,

,

.

Кроме того, . Значит, , и .

В общем случае имеет место следующая фундаментальная теорема (Silverman J.H. (editor) Cryptography and lattices conference. Proceedings of CALC 2001, to appear as a volume in Lecture notes in computer science, 1986).

ТЕОРЕМА. Для любой эллиптической кривой над полем существуют натуральные такие, что .