Билет 24. Нахождение асимптот графика функции

 Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные , наклонные .

Очевидно, горизонтальные являются частными случаями наклонных (при ).

 

 

 

 

 

 

 

 

 

 

 

Нахождение асимптот графика функции основано на следующих утверждениях.

Теорема 1. Пусть функция определена хотя бы в некоторой полуокрестности точки и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен или . Тогда прямая является вертикальной асимптотой графика функции.

Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Теорема 2. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции . Тогда прямая есть горизонтальная асимптота графика функции .

Может случиться, что , а , причем и - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов или , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.

Теорема 3. Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы и . Тогда прямая является наклонной асимптотой графика функции .

Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

Пример. Найдите все асимптоты графика функции .

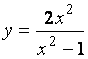Решение.

Функция определена при . Найдем ее односторонние пределы в точках .

Так как и (два других односторонних предела можно уже не находить), то прямые и являются вертикальными асимптотами графика функции.

Вычислим

(применим правило Лопиталя) =

.

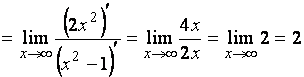Значит, прямая - горизонтальная асимптота.

Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).

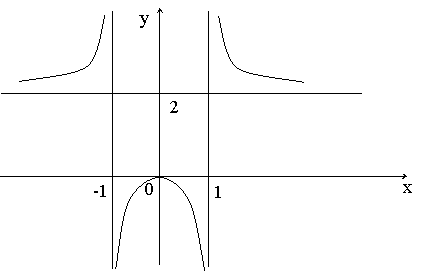Ответ: график имеет две вертикальные асимптоты и одну горизонтальную .

Билет 25. Первообразная. Неопределенный интеграл

 Определение 1. Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции.

(F(x))' = f(x).

Теорема 1 (теорема Коши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную.

Пример. Функция F(x)=x³ является первообразной функции f(x)=3x² так как (x³)'=3x². Функции F₁(x)=x³ +3 и F₂(x)=x³ - 2 также являются первообразными функции f(x). Любая функция вида F(x)=x³ +с, где с – произвольное число, является первообразной функции f(x).

Каждая функция может иметь бесконечно много первообразных, которые отличаются на постоянное слагаемое. Верно и обратное утверждение.

Теорема 2. Если F₁(x) и F₂(x) - две первообразные для функции f(x), то они отличаются на постоянное слагаемое.

Доказательство. Рассмотрим функцию

Ф(х) = F₁(x) - F₂(x).

Ф'(х) = F₁'(x) - F₂'(x) = f(x) - f(x) =0,

Ф(х) = C,

F₁(x) = F₂(x) +C.

Определение 2. Совокупность всех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается ò f(x)dx, где f(x) именуется подынтегральной функцией, выражение f(x)dx - подынтегральным выражением.

Если F(x) - некоторая первообразная данной функции, то

ò f(x)dx = F(x) + C, где C - произвольная постоянная.

Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции.

Первообразные имеют следующий геометрический смысл.

Пусть F₁(x) и F₂(x) - первообразные функции y=f(x). Найдем их производные в точке х₀ .

F₁'(х₀) = f(х₀) , касательные к графикам функций y = F₁(x) и y = F₂(x) F₂'(х₀) = f(х₀) , в любой точке параллельны.

Следовательно, и сами графики будут располагаться параллельно.

На основании теоремы 2 F₁(x) и F₂(x) отличаются на постоянное слагаемое, следовательно, один график можно получить из другого сдвигом на C единиц вдоль оси ОY.

F₁(x) = F₂(x) + C.

 

 

 

 

 

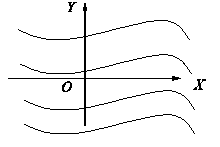
Функция имеет бесконечно много первообразных, которые отличаются друг от друга на постоянное слагаемое. Графики всех первообразных представляют собой бесконечное семейство параллельных кривых, которые заполняют всю плоскость. Через каждую точку плоскости проходит график одной из первообразных.