Задача о касательной

 

Пусть дана некоторая непрерывная функция . Графиком ее будет какая-то кривая .

В ыберем на кривой произвольную точку и, зафиксировав ее, возьмем на этой же кривой произвольным образом еще одну точку

Проведем секущую Станем затем приближать точку к точке по кривой (на чертеже точки , ). Секущая будет при этом поворачиваться.

Может случиться, что при неограниченном приближении точки к по кривой (с любой стороны) секущая будет стремиться к некоторому предельному положению.

Тогда предельное положение секущей и называется касательной к кривой в данной ее точке .

При этом, говоря о предельном положении секущей , мы имеем в виду следующее: существует такая прямая , что угол между нею и секущей (точнее говоря, один из этих углов) стремится к нулю, когда длина хорды стремится к нулю: .

Введя это определение, рассмотрим задачу о проведении касательной к данной кривой . Предположим, что эта кривая имеет в данной точке касательную , образующую с положительным направлением оси угол , отличный от прямого. Задача будет решена, если найдем угловой коэффициент касательной .

 

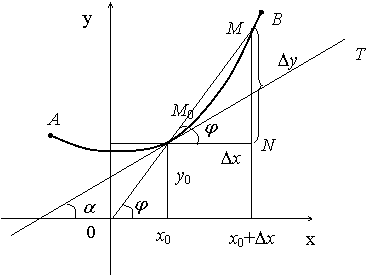
 Для решения этой задачи поступим следующим образом: дадим приращение и, вычислив соответствующее приращение функции , возьмем на кривой точку .

Проведем затем секущую . Пусть она образует с положительным направлением оси угол (он может быть как больше, так и меньше угла ). Для угла между секущей и касательной имеем: , откуда по определению касательной , или .

Так как кривая пересекается всякой прямой, параллельной оси , не более чем в одной точке, то для прямой угол отличен от прямого и существует. Проведем на рисунке и из найдем .

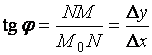Устремим теперь к нулю. Тогда в силу непрерывности функции и будет стремиться к нулю.

Отсюда , т.е. при и . Но при имеем: и вследствие непрерывности тангенса . Отсюда следует, что существует и предел , который также равен , т.е. существует , так что .

Итак, чтобы найти угловой коэффициент касательной в точке к кривой , где - непрерывная функция, достаточно уметь находить предел вида:

.

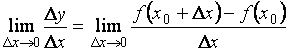Билет 11.Определение: Производной у= f(x) в т. Хо называется предел отношения приращения функции к приращению аргумента при Δx → 0 ,если такой предел существует и конечен.

Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ):

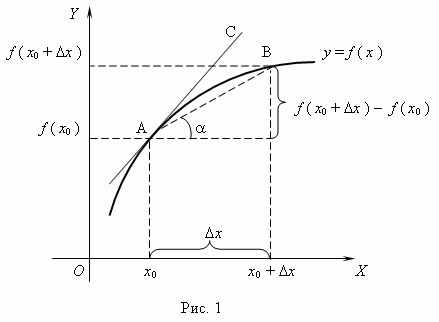
Из рис.1  видно, что для любых двух точек A и B графика функции:  

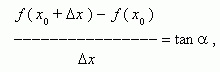
где  - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то  неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Механический(физический) смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +   точка перемещается на расстояние:  x ( t₀ + )  x ( t₀ ) = , а её средняя скорость равна:  v_a =  . При  0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид:

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Билет 12. Односторонние и бесконечные производные.

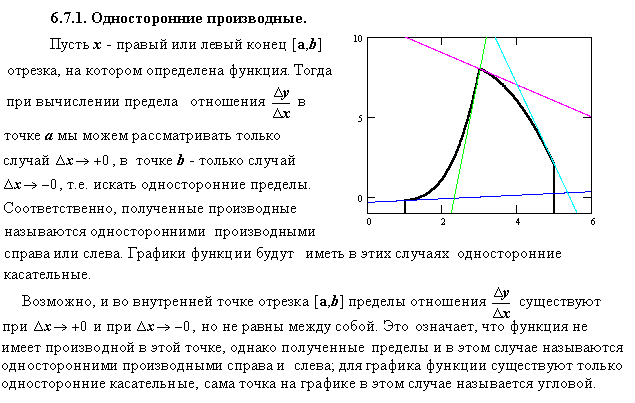
 Возможно, и во внутренней точке отрезка [a,b] пределы отношения   существуют при  и при , но не равны между собой. Это означает, что функция не имеет производной в этой точке, однако полученные пределы и в этом случае называются односторонними производными справа и слева; для графика функции существуют только односторонние касательные, сама точка на графике в этом случае называется угловой.

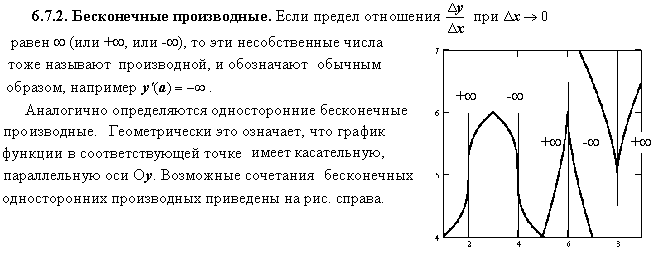
Определение: Функция назыв. дифференцируемой в т. х, если она имеет в этой точке конечную производную. Недифференц.- в этой точке не сущ. или обращается в бесконечность.

Билет 13.Теорема:Если функция дифференц. в т. х ,то она в этой точке и непрерывна. А если она в этой точке разрывна, то уже не дифференцирована.

Функция может быть разрывна, но дифференцируемой не является.

Билет 14.

Правила дифференцирования суммы, произведения и частного двух дифференцируемых функций.

 

Теорема Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы: 1) (u±v)/=u/±v/, 2) (u·v)/=u/v+v/u, 3) (vu)=v2u/v−v/u.

Доказательство Из определения производной:

(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]= =limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]= . 

=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/

(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+  

+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.

(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u.

Теорема доказана.

Билет 15.