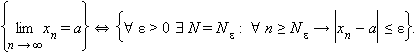Билет 1.Понятие функции- Пусть Х и Y - некоторые множества.

Определение 1. Если каждому элементу xÎХ ставится в соответствие по некоторому правилу единственный элемент yÎ Y , то говорят, что на множестве Х задана функция (отображение) со значениями в множестве Y :

f : X®Y, y=f(x).

Функция-переменная величина у назыв. функцией переменной вел-ны х, если кажд. х малое из Х по некоторому правилу поставлено соответ. определенному и единственному значению у из У.

Способы задания функции:

Аналитический, графический, табличный, логический.

Классификация функций:

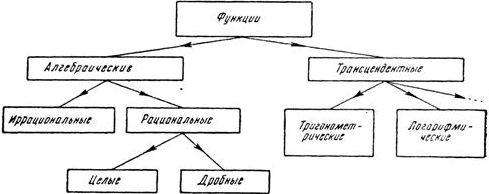
Элементарные- функции, получающиеся из основных элементарных функций с помощью конечного числа алгебраических операций и конечного числа операций образования сложной функции.

Сложная функция- Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = φ(х), то у является С. ф. от х, то есть y = f [(x)], определённой для тех значений х, для которых значения φ(х) входят в множество определения функции f (u). В таком случае говорят, что у является С. ф. независимого аргумента х, а u — промежуточным аргументом.

Проще говоря, сложная функция-это функция от функции ))))

Билет 2.Числ. послед-ть- Определение. Если каждому числу n натурального ряда чисел 1, 2, ..., n, ... ставится в соответствие по определенному закону некоторое вещественное число , то множество вещественных чисел , , , ..., мы назовем числовой последовательностью или просто последовательностью. Сокращенно последовательность обозначается .

Предел числ. послед-ти- Число a называется пределом последовательности {x_n}, если для каждого ε > 0 существует такой номер N_ε, что для всех n ≥ N_ε выполняется неравенство

|xn – a| < ε,

т. е. При этом пишут, что 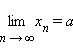или при n → ∞. Кратко это определение можно записать так:

Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности такой, что сходящейся к числу a, соответствующая последовательность значений функции сходится к числу A.

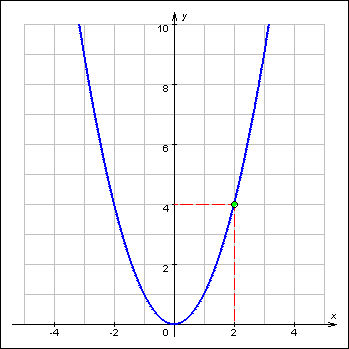
График 1.3.6.1.

Предел функции y = x² при x → 2.

График 1.3.6.2.

Предел функции  при x → 0.

Если A – предел функции в точке a, то пишут, что

Билет 3.

Бесконечно малые функции- Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Бесконечно большие функции- тоже самое, но если предел равен минус или плюс бесконечности.

Свойства:

1. Алгебраическая сумма конечного числа б.м. функций есть б.м.

2. Произведение двух б.м. функций есть б.м. функция

3. Произведение ограниченной функции на б.м. есть б.м.

4. Произведение б.м. на число есть б.м.

5. Частное от деления малой функции на функцию, имеющую отличный от нуля предел, есть б.м.

Св-ва б.б- такие же, только наоборот

Теорема о связи между бесконечно большой и бесконечно малой функциями:

Если функция - функция бесконечно малая ( ), то функция есть бесконечно большая функция и наоборот.

Доказательство:

Пусть - бесконечно малая функция при , т.е. . Тогда для любого числа существует такое число , что для всех , удовлетворяющих неравенству , выполняется неравенство , т.е. , т.е. , где . А из этого следует, что функция - бесконечно большая.

Теорема о связи функции с ее пределом

Для того чтобы необходимо и достаточно выполнение равенства где — б.м. при х а

— б.м., х а)

Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:

Сравнение бесконечно малых

Пусть и — бесконечно малые при . 1. Если , то говорят, что является бесконечно малой высшего порядка по сравнению с . В этом случае пишут . 2. Если , где —число, отличное от нуля, то говорят, что и — бесконечно малые одного и того же порядка. В часности, если , то бесконечно малые и называются эквивалентными. Запись ~ означает, что и —эквивалентные бесконечно малые.          Если , то это означает, что . Таким образом, является бесконечно малой высшего порядка по сравнению с , т. е. 3. Если и —бесконечно малые одного и того же порядка, причем , то говорят, что бесконечно малая имеет порядок по сравнению с .

Билет 4. Основные теоремы о пределах

 

Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

Þ .

Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

Þ .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x)=с, докажем, что .

Возьмем произвольное e>0. В качестве d можно взять любое

положительное число. Тогда при

.

Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

и .

По теореме о связи предела и бесконечно малой функции:

f(x)-A= - б.м. при ,

f(x)-B= - б.м. при .

Вычитая эти равенства, получим:

B-A= - .

Переходя к пределам в обеих частях равенства при , имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство. Пусть , , .

Тогда, по теореме о связи предела и б.м. функции:

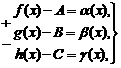где - б.м. при .

Сложим алгебраически эти равенства:

f(x)+g(x)-h(x)-(А+В-С)= ,

где б.м. при .

По теореме о связи предела и б.м. функции:

А+В-С= .

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при , причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при , причем предел частного равен частному пределов.

,

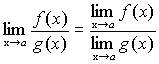Признаки существования предела

 

Теорема 1 (теорема о двух милиционерах). Если функция y=f(x) в некоторой окрестности точки а заключена между двумя функциями и , т.е. выполняется неравенство "х, причем эти функции имеют одинаковый предел при , то существует предел функции y=f(x) при , равный этому же значению.

,

=> .

Теорема 2. Если функция y=f(x) монотонно возрастет (убывает) в некоторой окрестности точки а и ограничена сверху (снизу), то она имеет предел при .