Тема 3. Теория потребительского поведения. Выбор и равновесие потребителя Примеры решения задач с комментариями

Задача 1.

Полезность семи конфет равна 20, а полезность восьми конфет – 24 ютилам. Оцените предельную полезность седьмой, восьмой и девятой конфеты.

Решение и комментарии.

Исходя из понятий общей и предельной полезности блага и условия задачи, можно рассчитать предельную полезность восьмой конфеты MU₈ по формуле:

MU₈ = TU₈ – TU₇,

где TU₈, TU₇ – общая полезность восьми, семи конфет.

Подставим значения и получим:

MU₈ = 24 – 20 = 4 ютил.

В соответствии с законом убывающей предельной полезности блага предельная полезность седьмой конфеты должна быть больше 4 ютил (MU₇ > 4), а девятой конфеты – меньше 4 ютил (MU₉ < 4).

Задача 2.

Первое яблоко доставляет H удовлетворение, равное 8u. Каждое следующее яблоко доставляет добавочное удовлетворение, на 2u меньше предыдущего. Начиная с какого яблока суммарное удовлетворение от потребления яблок будет уменьшаться?

Решение и комментарии.

Предельная полезность задается формулой убывающей арифметической прогрессии с первым членом 8 и разностью 2, которая записывается следующим образом:

MU_i = 10 – 2i,

где i – количество единиц потребляемого блага (яблока).

Соотношение общей (TU) и предельной полезности (MU_i) проявляется в росте общей полезности до ее максимального значения с последующим ее снижением и одновременно в снижении предельной полезности до нулевого и последующего отрицательного значения по мере увеличения потребления добавочной единицы блага. Исходя из этого найдем переломную точку описанного соотношения, когда TU = max и MU_i = 0, решив уравнение 10 – 2i = 0 (или неравенство 10 – 2i < 0). Отсюда i = 5, т.е. начиная с шестого яблока общая полезность уменьшается.

Задача 3.

Цена товара А составляет 3 руб., цена товара В – 1,5 руб. Потребитель желает максимизировать удовлетворение от покупки товаров А и В. При этом он оценивает предельную полезность товара В в 60 единиц (ютил). Как потребитель оценит предельную полезность товара А.

Решение и комментарии.

Рациональный потребитель максимизирует удовлетворение от покупки товаров А и В, руководствуясь правилом максимизации полезности, которое можно выразить следующей формулой:

где MU_A, MU_В – предельные полезности товаров А, В; Р_А, Р_В – цены товаров А, В.

Подставив значения, находим

Задача 4.

Потребитель делает выбор между товарами А и В. Его доход составляет 13 руб., цена товара А равна 3 руб., товара В – 2 руб. Ниже в табл. 3.1 приведена предельная полезность товаров А и В (MU_A, MU_В). Определить:

1) количество единиц каждого товара, которое потребитель купит, чтобы максимизировать полезность;

2) величину общей полезности, которую потребитель получит.

Таблица 3.1

Единица товара А и В (Qi)	MUA	MUВ
1	30	22
2	21	12
3	15	6
4	12	4

Решение и комментарии.

Чтобы максимизировать полезность потребляемых благ А и В, потребитель должен на свой доход в 13 руб. купить такое количество единиц товара А и В, каждая из которых принесла бы наибольшую предельную полезность на каждый затраченный рубль. Для этого нужно рассчитать взвешенные предельные полезности каждой единицы товара А и В по формулам 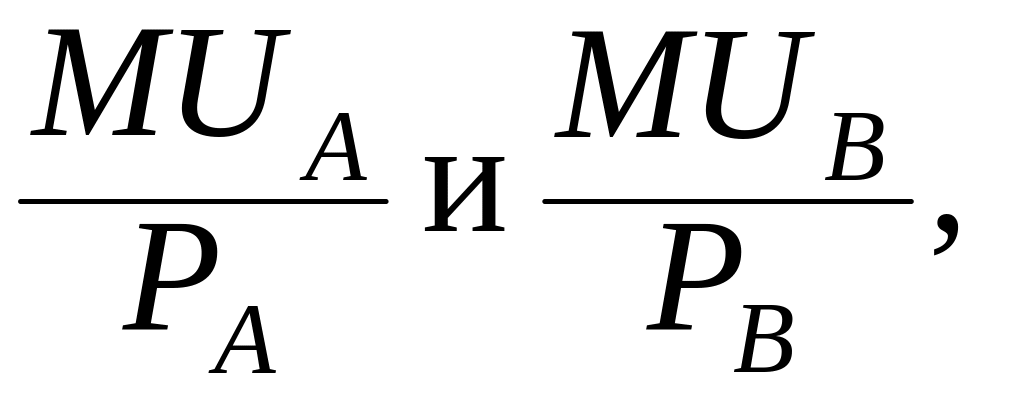где Р_А, Р_В – цены товаров А и В. Результаты расчетов поместим в табл. 3.2.

Расчет общей полезности от потребления товаров А и В произведем по формуле:

TU = MU₁ + MU₂ + MU₃ + MU₄,

где MU₁, MU₂, MU₃, MU₄ – предельные полезности первой, второй, третьей, четвертой единицы потребляемых благ А или В.

Сопоставляя взвешенные предельные полезности каждой потенциально приобретаемой единицы товаров А и В ( ), потребитель выбирает благо с наибольшим ее значением с учетом цены блага и величины бюджетного ограничения (дохода) потребителя.

В табл. 3.3 представлена последовательность действий потребителя в процессе выбора приобретаемого набора благ А и В.

Таблица 3.2

Единицы товара А и В	MUA	MUA/PA	TUA	MUВ	MUВ/PВ	TUВ
1	30	10	30	22	11	22
2	21	7	51	12	6	34
3	15	5	66	6	3	40
4	12	4	78	4	2	44

Последовательность покупок:

Таблица 3.3

Возможности выбора товаров	MUA/PA; MUВ/PВ	Решение потребителей	Остаток дохода
1. 1-я ед. товара А	10	1-я ед. товара В за 2 руб.	13 - 2 = 11 руб.
1-я ед. товара В	11
2. 1-я ед. товара А	10	1-я ед. товара А за 3 руб.	11 - 3 = 8 руб.
2-я ед. товара В	6
3. 2-я ед. товара А	7	2-я ед. товара А за 3 руб.	8 - 3 = 5 руб.
2-я ед. товара В	6
4. 3-я ед. товара А	5	2-я ед. товара В за 2 руб.	5 - 2 = 3 руб.
2-я ед. товара В	6
5. 3-я ед. товара А	5	3-я ед. товара А за 3 руб.	3 - 3 = 0 руб.
3-я ед. товара В	3

Результаты выбора следующие:

1) 3 единицы товара А и 2 единицы товара В;

2) общая полезность выбранного товарного набора составит: 3А + 2В = 66 + 34 = 100 ютил.

Задача 5.

Потребитель находится в состоянии равновесия при следующей структуре его покупок: 2 кг овощей по 3 ден. ед. за килограмм и 4 кг фруктов по 5 ден. ед. Определите предельную норму замещения фруктов овощами и бюджетное ограничение потребителя.

Решение и комментарии.

Предельная норма замены (MRS) фруктов овощами определяется отношением цен этих товаров:

где Р_ов, Р_фр. – цены овощей, фруктов за 1 кг.

То есть при увеличении потребления овощей на 1 кг потребление фруктов должно быть сокращено на 0,6 кг.

В соответствии с понятием бюджетного ограничения запишем уравнение бюджетной линии и определим величину бюджетного ограничения потребителя по формуле:

I = P_ов. · x_ов. + P_фр. · y_фр.,

где x_ов., y_фр. – количество (килограммов) овощей, фруктов.

I = 3 · 2 + 5 · 4 = 26.

То есть бюджет потребителя составляет 26 ден. ед.

Задача 6.

Потребитель К считает, что ему одинаково полезно еженедельно выпивать как 8 стаканов молока и 3 стакана кефира, так и 6 стаканов молока и 4 стакана кефира. Определить предельную норму замены кефира на молоко.

Решение и комментарии.

В соответствии с определением предельной нормы замены одного блага на другое (MRS_ху) и условием данной задачи предельной нормой замены кефира на молоко является количество стаканов кефира, которое должно быть сокращено при увеличении потребления молока на 1 стакан по формуле:

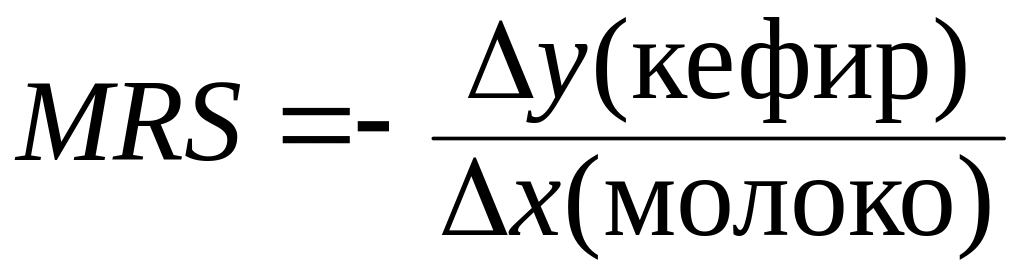при u = const,

где Δy – сокращение потребления кефира; Δx – увеличение потребления молока.

Подставив значения, получим: Это значит, что для сохранения неизменного уровня полезности потребитель К, еженедельно выпивая седьмой, восьмой стакан молока, сокращает потребление кефира по 0,5 стакана.

Задача 7.

На рис. 3.1 показана одна из кривых безразличия некоего потребителя и его бюджетная линия. Доход потребителя составляет 150 ден. ед. Напишите уравнение бюджетной линии.

Рис. 3.1. Кривая безразличия (U) и бюджетная линия (BL)

Решение и комментарии.

Уравнение бюджетной линии формируется исходя из понятия бюджетного ограничения потребителя, бюджетной линии и ее графического изображения.

Бюджетное ограничение указывает, что общий расход потребителя на приобретение благ х и у должен быть не больше его дохода. Весь фиксированный доход (I) потребитель тратит на покупку товаров х и у в количестве Q_x и Q_y по ценам Р_х и Р_у, поэтому бюджетное ограничение может быть записано так: I = P_x · Q_x + P_y · Q_y. Решив это уравнение относительно Q_y, получим уравнение бюджетной линии:

Отношение показывает точку пересечения бюджетной линией BL оси у, которой соответствует количество приобретаемого товара у (Q_y), равное 30 ед., при полном использовании на него дохода I = 150 ден. ед. (Q_x = 0). Подставив соответствующие значения в выражение получим откуда Р_у = 5 ден. ед. Аналогично определим цену товара х (Рх) из отношения которое показывает точку пересечения BL оси х: откуда Рх = 3 ден. ед.

Полученные значения подставим в уравнение бюджетной линии и упростим его:

Задача 8.

На графике показана кривая безразличия потребителя и его бюджетная линия. Цена товара А – 18 руб. Определить, какова цена товара В. Как изменится положение бюджетной линии:

1) при увеличении цены товара А до 30 руб.?

2) при снижении цены товара А до 15 руб.?

Рис. 3.2. Кривая безразличия (U) и бюджетная линия (BL)

Решение и комментарии.

На графике изображена ситуация потребительского равновесия, при которой потребитель получил максимальное удовлетворение U от приобретенных благ А и В в количестве, соответственно, 30 и 36 штук, полностью израсходовав свой доход, величина которого неизвестна. Величину дохода (I) можно определить, используя выражение бюджетного ограничения (см. задачу 7):

I = P_A · Q_A + P_B · Q_B; если Q_B = 0, то I = P_A · Q_A = 18 · 50 = 900 руб.

Отсюда цена товара В:

Изменение положения бюджетной линии:

1) при P_A = 30 руб. потребитель на свой доход I = 900 руб. сможет приобрести 30 ед. товара А и бюджетная линия сместится в положение BL₁ (рис. 3.3);

Рис. 3.3. Изменение положения бюджетной линии

при увеличении цены товара А

2) при Р_В = 15 руб. потребитель на свой доход I = 900 руб. сможет приобрести 60 ед. товара А и бюджетная линия сместится в положение BL2 (рис. 3.4).

Рис. 3.4. Изменение положения бюджетной линии

при снижении цены товара А