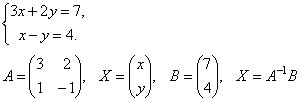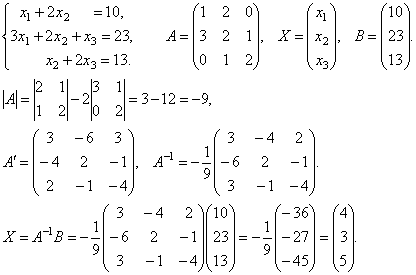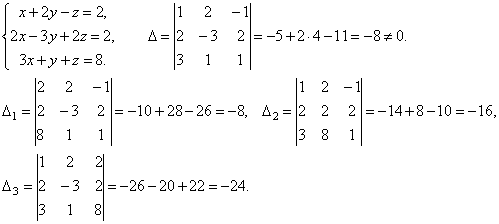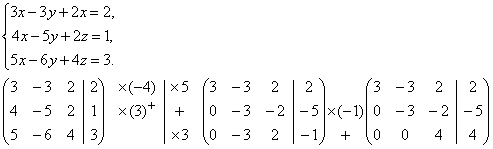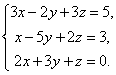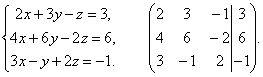8.6. Исследование системы двух линейных уравнений с двумя неизвестными

Учитель:

Исследовать систему уравнений — значит определить, имеет ли она решения и, если имеет, то сколько.

Мы уже исследовали систему двух линейных уравнений с двумя неизвестными с помощью графиков (см. п.2 этой главы). Там же было установлено, что в зависимости от количества решений бывают определенные, неопределенные и несовместные системы. Теперь посморим, как зависят эти три случая от коэффициентов. В каждом уравнении хотя бы один из коэффициентов при неизвестном не равен нулю (иначе не будет и системы). Для решения системы умножим первое уравнение на  , а второе на   и, сложив их, получим  . Умножив первое уравнение на  , а второе на  , и сложив уравнения, получим:  . Два полученных уравнения образуют систему, равносильную данной системе.

Обрати внимание на то, что двучленный коэффициент при   и при   одинаковый. Его называют главным определителем системы, обозначают символом   (дельта).

Его легко составить по данной системе с помощью следующей таблицы:  .

Ученик:

Значит, чтобы составить определитель, надо просто выписать коэффициенты при   и при   из нашей исходной системы? Я правильно понимаю?

Учитель:

Молодец, все верно.

Продолжим исследовать систему.  Чтобы из таблицы получить двучлен, надо из произведения коэффициентов (  и  ), стоящих по так называемой главной диагонали, вычесть произведение коэффициентов, стоящих по другой диагонали таблицы. Если   и   в первом столбце таблицы главного определителя заменим на   и  , то получим таблицу первого вспомогательного определителя  : . Аналогично получим второй вспомогательный определитель системы: . Теперь полученная система, которая дает нам решение данной вначале системы, записывается очень кратко, легко запоминается и дает готовые формулы для решения системы:  и  .

Ученик:

А для чего мы вообще находим эти  ? Что нам это дает?

Учитель:

Так мы можем определить к какому типу относится система.  Мы получаем три случая: а) если главный определитель системы   не равен нулю, то система определенная, т.е. имеет единственное решение:  и  ; б) если  , то наша система принимает вид:   и   и теперь все зависит от вспомогательных определителей   и  .  Если при   хотя бы один из определителей   и   не равен нулю, то решения нет и система несовместна (левые части   и   равны нулю, а правая часть не равна нулю, что невозможно); в) если   и  , то система принимает вид:   и  , имеет бесконечное множество решений и является неопределенной. Одному из неизвестных можно дать любое значение, подставить его в одно из уравнений системы и вычислить соответствующее значение другого неизвестного.

Билет№20

Системой m линейных уравнений с n неизвестными называется система вида

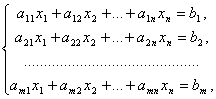
где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 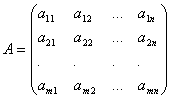 , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например, 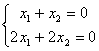 . Решением этой системы является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например, 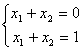 , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

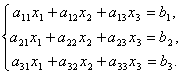
Рассмотрим матрицу системы 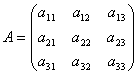  и матрицы столбцы неизвестных и свободных членов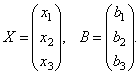 

Найдем произведение

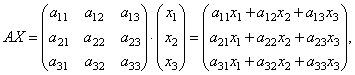
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

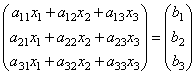 или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A:  . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

1. 

Найдем матрицу обратную матрице A.

, 

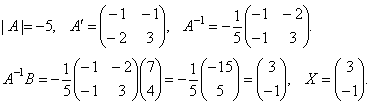
Таким образом, x = 3, y = – 1.

2. 

Итак, х₁=4,х₂=3,х₃=5.

3. Решите матричное уравнение: XA+B=C, где 

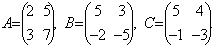
Выразим искомую матрицу X из заданного уравнения.

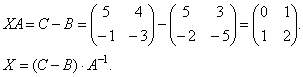
Найдем матрицу А^-1.

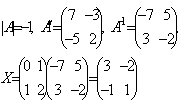
Проверка:

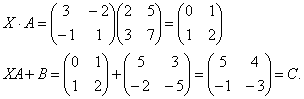
4. Решите матричное уравнение AX+B=C, где 

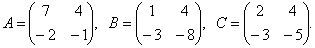
Из уравнения получаем  .

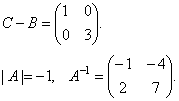
Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

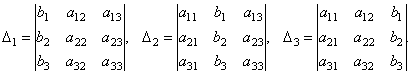
Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – наA₂₁ и 3-е – на A₃₁:

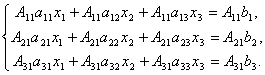
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

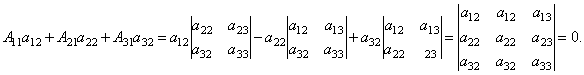
Аналогично можно показать, что и  .

Наконец несложно заметить, что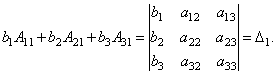 

Таким образом, получаем равенство:  .

Следовательно,  .

Аналогично выводятся равенства   и  , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

1. 

Итак, х=1, у=2, z=3.

2. Решите систему уравнений при различных значениях параметра p: 

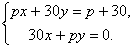
Система имеет единственное решение, если Δ ≠ 0.

. Поэтому  .

1. При 

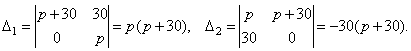
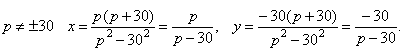
2. При p = 30 получаем систему уравнений 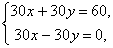  которая не имеет решений.

3. При p = –30 система принимает вид 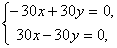  и, следовательно, имеет бесконечное множество решений x=y, yR.

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

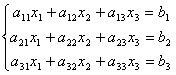Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

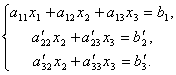
Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на  , умножим на  и сложим со вторым. Тогда будем иметь систему уравнений:

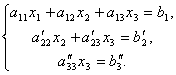
Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;

2. умножение строки на число, отличное от нуля;

3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

1. 

Вернувшись к системе уравнений, будем иметь

2. 

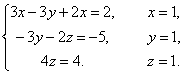
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

3. 

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – приx.

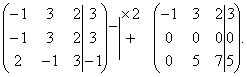
Вернемся к системе уравнений.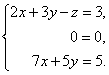 

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

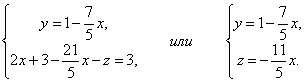
Таким образом, система имеет бесконечное множество решений

Билет№21

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2]. Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Пример 2.13. Решить систему уравнений методом Гаусса:

                                                      x +  y - 3z = 2,

                                                    3x - 2y +  z = - 1,

                                                    2x +  y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

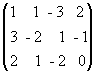
и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~  ;

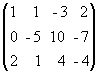б) третью строку умножим на (-5) и прибавим к ней вторую:

.

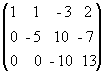В результате всех этих преобразований данная система приводится к треугольному виду:

                                                    x + y - 3z = 2,

                                                    -5y + 10z = -7,

                                                           - 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = - 0,7.

Билет№22

Метод Гаусса — Жордана используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь Гаусса и Жордана.