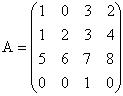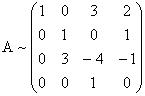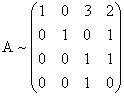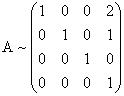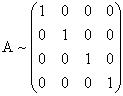1.6. Векторы
Если матрица состоит только из одного столбца (J = 1), то такой объект называется вектором. Точнее говоря, вектором-столбцом. Например
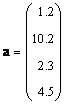
Можно рассматривать и матрицы, состоящие из одной строки, например
Этот объект также является вектором, но вектором-строкой. При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.
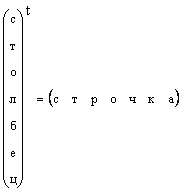
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0.
Содержание
1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,
Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными, если существует такое число α, что
αx = y.
Билет№18
|
Дана прямоугольная матрица
Выделим в этой матрице k произвольных строк и k произвольных столбцов. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Матрица А имеет Сkm·Сkn миноров k-го порядка.
Рассмотрим всевозможные миноры матрицы А, отличные от нуля.
Рангом матрицы А называется наибольший порядок невырожденного минора этой матрицы. Если матрица нулевая, то ранг ее принимается равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы А обозначается r(A). Если r(A) = r(B), то матрицы А и В называются эквивалентными. В этом случае пишут А ~ В.
Под элементарными преобразованиями матрицы понимают: 1) замену строк столбцами, а столбцов - соответствующими строками; 2) перестановку строк; 3) вычеркивание строки, все элементы которой равны нулю; 4) умножение какой-либо строки на число, отличное от нуля; 5) прибавление к элементам одной строки соответствующих элементов другой. Пример. Найти ранг матрицы
Решение. Первую строку перепишем. От элементов второй строки вычтем соответствующие элементы первой строки и запишем во вторую строку. От элементов третьей строки вычтем соответствующие элементы первой строки, умноженные на 5. Четвертую строку перепишем.
Первую строку перепишем. Вторую и третью строки разделим на 2 и запишем соответственно на место второй и третьей строки. Четвертую строку перепишем.
Первую, вторую и червертую строки перепишем. На место третьей строки поставим разность третьей и второй, умноженной на 3.
Первую, вторую и червертую строки перепишем. Третью строку разделим на (-4).
От первой строки отнимем четвертую, умноженную на 3. Вторую строку перепишем. На место третьей строки поставим четвертую. На место четвертой строки поставим разность третьей и четвертой.
От первой строки вычтем четвертую, умноженную на 2. От второй строки вычтем четвертую. Третью и четвертую строки перепишем.
Ранг данной матрицы равен 4, т.к. получили единичную квадратную матрицу четвертого порядка (определитель единичной матрицы всегда равен 1, т.е. отличен от нуля, что по определению означает, что матрица невырожденная). |
Билет№19