Парабола

Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением

y2 = 2px,

(1)

где p>0 — параметр параболы. Это уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.

Заметим, что в канонической системе ось OX является осью симметрии параболы. Следовательно, мы можем ограничиться исследованием функции

y = √ 2px

(2)

при 0 ≤ x< + ∞ , т.е. рассматривать часть параболы, лежащую в первой четверти, а затем полученную кривую отразить симметрично относительно оси OX .

Область определения функции (2): 0 ≤ x< + ∞ , область значений функции(2): 0 ≤ y< + ∞ . Вычислив y' и y'' , легко убедиться в том, что функция (2) в интервале x  (0, + ∞) возрастает от нуля до + ∞ и ее график является выпуклым вверх. Асимптот у параболы нет. Начало координат (0, 0) — вершина параболы (рис. 1).

Прямая x = −p/2 называется директрисой параболы, а точка (p/2, 0) —ее фокусом.

Уравнения y² = −2px , x² = 2py и x² = −2py (p>0) также описывают параболы, ветви которых направлены влево, вверх и вниз, соответственно

Билет№14

Общее уравнение линии второго порядка имеет вид

Ax² + 2Bxy + Cy² + Dx + Ey + F = 0.

Задача упрощения этого уравнения состоит в том, чтобы в преобразованном уравнении были устранены: 1) член, содержащий произведение текущих координат, и 2) члены, содержащие первые степени двух координат или, по крайней мере, одной из них.

В том случае, когда уравнение линии второго порядка содержит произведение текущих координат, упрощение его следует начинать с поворота осей без изменения начала координат и надлежащим выбором угла поворота добиться того, чтобы из преобразованного уравнения был устранен член, содержащий произведение текущих координат. Преобразование координат в этом случае будем вести по формулам

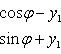
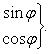
Если после устранения из преобразованного уравнения члена с произведением текущих координат в нем останутся члены с первыми степенями текущих координат, то последующим параллельным переносом осей можно, как это было показано, привести уравнение к каноническому виду.

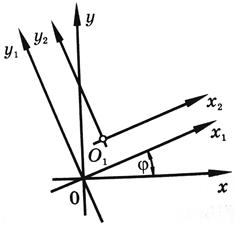
Координатную систему, полученную в результате поворота первоначальной системы координат, будем обозначать через x₁Oy₁, а систему координат, полученную от параллельного переноса координатной системы x₁Oy₁, - через x₂O₁y₂ (см. рисунок)

 

Билет№16

Матрицы и операции над ними*

Далее будем рассматривать квадратные матрицы   и   (квадратные таблицы чисел с двумя строками и тремя  столбцами и тремя строками и тремя столбцами). Все, что будет говориться, справедливо и для квадратных матриц порядка  .

Определение. Две матрицы называются равными, если у них совпадают элементы, стоящие на одинаковых местах.

Определим сумму двух матриц. Пусть

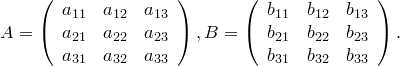
Тогда суммой матриц   и   называется матрица

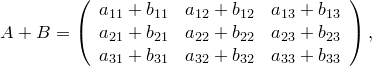
произведением матрицы   на вещественное число   — матрица

произведением строки   на столбец 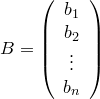  — число

произведением матриц   и   — матрица

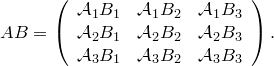
Здесь   —  -я строка матрицы  ,   —  -ый столбец матрицы  .

Свойства операций над матрицами

1.  . 2.  . 3. Матрица  , состоящая из нулей, играет роль нуля:   для любой  . 4. Противоположная матрица для матрицы   — матрица  :  . 5.  . 6.  . 7.  . 8.  .

Умножение матриц не коммутативно!

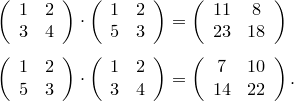
Свойства умножения матриц

1.  . 2.  . 3.  . 4.  .

Определение. Единичной матрицей называется матрица, у которой элементы главной диагонали равны 1, а все остальные элементы — нули:

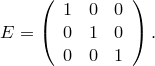
Очевидно, что  .

Билет№17

Рассмотрим квадратную матрицу

  .

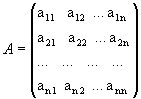Обозначим Δ =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, илиособенной, если Δ = 0.

Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Обратная матрица матрице А, обозначается через А^1, так что В = А^1 и вычисляется по формуле

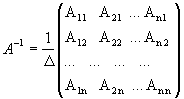,                                               (1)

где А _{i j} - алгебраические дополнения элементов a _{i j} матрицы A..

Вычисление A^-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A^-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицыможно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Пример 2.10. Для матрицы 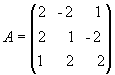  найти A^-1.

Решение. Находим сначала детерминант матрицы А 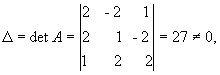     значит, обратная матрица существует и мы ее можем найти по формуле: 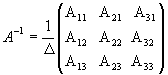  , где А_{i j} (i,j=1,2,3) - алгебраические дополнения элементов а_{i j} исходной матрицы.                    

                    

                   

                  

 откуда    .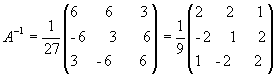

Пример 2.11. Методом элементарных преобразований найти A^-1 для матрицы: А=  .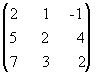

Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 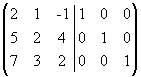 . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.  Для этого поменяем местами первый и второй столбцы: 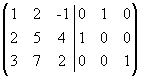  . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 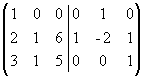 . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй; 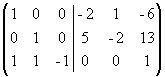 . Прибавим третий столбец к первому и второму: 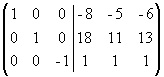 . Умножим последний столбец на -1:  . 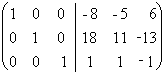Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,           .
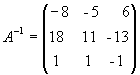