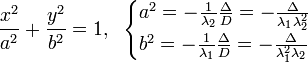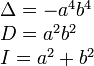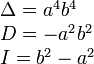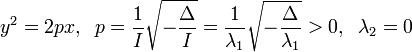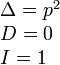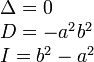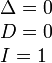- •Свойства умножения вектора на число:
- •Свойства скалярного произведения:
- •Билет №2 Линейная зависимость векторов
- •Компланарность Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости. Свойства компланарности
- •Скалярное произведение векторов
- •Свойства векторного произведения: Действия над векторами
- •Свойства операции сложения:
- •Свойства умножения вектора на число:
- •Прямая на плоскости Любая прямая на плоскости может быть задана уравнением первого порядка
- •Парабола
- •Матрицы и операции над ними*
- •1.6. Векторы
- •1.7. Простейшие операции с векторами
- •8.6. Исследование системы двух линейных уравнений с двумя неизвестными
- •Алгоритм Править
Свойства векторного произведения: Действия над векторами
Определение
Вектором называется
направленный отрезок ![]() ,
где точка
,
где точка ![]() -
начало, точка
-
начало, точка ![]() -
конец вектора.
-
конец вектора.
Суммой ![]() векторов
и
называют
такой третий вектор
,
начало которого совпадает с началом
,
а конец - с концом
при
условии, что конец вектора
и
начало вектора
совпадают.
векторов
и
называют
такой третий вектор
,
начало которого совпадает с началом
,
а конец - с концом
при
условии, что конец вектора
и
начало вектора
совпадают.
Свойства операции сложения:
1° - коммутативность
2° - ассоциативность
3°
4°
Определение
Разностью векторов и называется вектор такой, что выполняется условие: .
Произведением вектора на число называется вектор , удовлетворяющий условиям:
, если , , если .
Свойства умножения вектора на число:
1°
2°
3°
4°
5°
6°
Приложение векторного произведения: Допустим, что нам дана геометрическая фигура (многоугольник, призма, пирамида) и известны координаты ее вершин. Тогда мы с помощьювекторной алгебры можем находить длины сторон (ребер), углы междуними, площади многоугольников, граней призмы или пирамиды, объемы.
1) Длина стороны (ребра) АВ.
Пусть ![]() ,
, ![]() .
Тогда
.
Тогда
![]() ,
,
где ![]() .
.
2) Угол между сторонами (ребрами) АВ и АС.
Пусть
,
, ![]() .
Тогда
.
Тогда
![]() ,
где
,
где
, ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
В
частности, ![]() ,
т.е.
,
т.е. ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() (при
условии, что
(при
условии, что ![]() и
и ![]() ).
).
3) Площадь параллелограмма АВСD.
![]()
![]() .
Т.к.
.
Т.к.
![]()
![]() ,
то осталось воспользоваться формулой
для вычисления модуля вектора.
,
то осталось воспользоваться формулой
для вычисления модуля вектора.
4) Площадь треугольника АВС.
![]() ,
,
где АВСD – параллелограмм, построенный на сторонах треугольника АВС.
5)
Объем параллелепипеда ![]() .
.
![]() .
.
6) Объем треугольной пирамиды SАВС.
![]() .
.
Докажем последнюю формулу. Объем пирамиды равен
![]() ,
где
,
где ![]() ,
а высота пирамиды равна
,
а высота пирамиды равна ![]() ,
откуда и следует доказываемая формула:
,
откуда и следует доказываемая формула:
![]()
![]() .
.
Билет№5
Смешанным
произведением трех векторов ![]() называется
число
называется
число
![]()
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.
П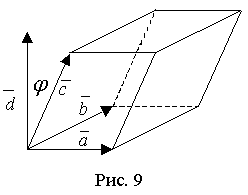 усть
правая
тройка векторов (рис. 9). Действительно,
объем параллелепипеда, построенного
на векторах
,
равен площади основания
усть
правая
тройка векторов (рис. 9). Действительно,
объем параллелепипеда, построенного
на векторах
,
равен площади основания ![]() на
высоту
на
высоту![]() .
Здесь φ - угол между векторами
.
Здесь φ - угол между векторами![]() и
и ![]()
Знак смешанного произведения совпадает со знаком cos φ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.
Если
перемножаемые векторы лежат в одной
плоскости (cos φ = 0), то ![]() -
необходимое и достаточное условие
компланарности векторов.
-
необходимое и достаточное условие
компланарности векторов.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат
![]()
Из 3.6.2 известно, что
![]()
Скалярно умножим этот вектор на вектор и, учитывая свойства скалярного произведения, получим
![]()
Это выражение может быть получено при вычислении определителя
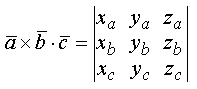
по элементам третьей строки, исходя из правила вычисления определителя.
![]()
Поэтому смешанное произведение трех векторов обозначают как , не подчеркивая при этом, какая пара векторов умножается векторно.
Билет№6
Прямая на плоскости Любая прямая на плоскости может быть задана уравнением первого порядка
Общее уравнение
Ax
+ By + C (![]() >
0).
>
0).
Вектор ![]() =
(А; В) -
нормальный вектор прямой.
=
(А; В) -
нормальный вектор прямой.
В
векторном виде: ![]() +
С = 0,
где
+
С = 0,
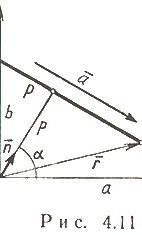
где ![]() -
радиус-вектор произвольной точки на
прямой (рис. 4.11).
-
радиус-вектор произвольной точки на
прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 - прямая параллельна оси Ox;
2) Ax + C = 0 - прямая параллельна оси Oy;
3) Ax + By = 0 - прямая проходит через начало координат;
4) y = 0 - ось Ox;
5) x = 0 - ось Oy.
Уравнение прямой в отрезках
![]()
где a, b - величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)
![]()
где ![]() -
угол, образуемый нормально к прямой и
осью Ox; p -
расстояние от начала координат до
прямой.
-
угол, образуемый нормально к прямой и
осью Ox; p -
расстояние от начала координат до
прямой.
Приведение общего уравнения прямой к нормальному виду:
![]()
Здесь ![]() -
нормируемый множитель прямой; знак
выбирается противоположным знаку C,
если
-
нормируемый множитель прямой; знак
выбирается противоположным знаку C,
если ![]() и
произвольно, если C
= 0.
и
произвольно, если C
= 0.
Билет№7
Две
прямые называются пересекающимися,
если они имеют одну единственную общую
точку. Эта общая точка двух прямых
называется точкой
пересечения прямых.
Точка пересечения разбивает каждую из
пересекающихся прямых на два луча.
Очевидно, эти лучи образуют четыре
неразвернутых угла, среди которых две
пары вертикальных углов и четыре пары
смежных углов. Таким образом, если нам
известна мера одного из углов, образованных
двумя пересекающимися прямыми, то мы
можем определить меры трех остальных
углов. Действительно, пусть один из
углов равен углу ![]() .
Тогда вертикальный с ним угол также
равен
,
а смежные с ним углы равны
.
Тогда вертикальный с ним угол также
равен
,
а смежные с ним углы равны ![]() .
Если
.
Если ![]() ,
то все четыре угла являются прямыми. В
этом случае пересекающиеся прямые
называются перпендикулярными (им
посвящена статья перпендикулярные
прямые).
Из приведенного определения следует,
что градусная мера угла между двумя
пересекающимися прямыми выражается
действительным числом из интервала
,
то все четыре угла являются прямыми. В
этом случае пересекающиеся прямые
называются перпендикулярными (им
посвящена статья перпендикулярные
прямые).
Из приведенного определения следует,
что градусная мера угла между двумя
пересекающимися прямыми выражается
действительным числом из интервала ![]() .
Угол между перпендикулярными прямыми
по определению равен девяноста градусам.
Мы
знаем, что от прямой линии на плоскости
в прямоугольной системе координат
неотделимнаправляющий
вектор прямой и нормальный
вектор прямой,
и мы можем по заданному уравнению прямой
на плоскости определить координаты ее
направляющего и нормального вектора.
Таким образом, у нас есть возможность
получить координаты направляющих и
нормальных векторов заданных пересекающихся
прямых.
.
Угол между перпендикулярными прямыми
по определению равен девяноста градусам.
Мы
знаем, что от прямой линии на плоскости
в прямоугольной системе координат
неотделимнаправляющий
вектор прямой и нормальный
вектор прямой,
и мы можем по заданному уравнению прямой
на плоскости определить координаты ее
направляющего и нормального вектора.
Таким образом, у нас есть возможность
получить координаты направляющих и
нормальных векторов заданных пересекающихся
прямых.
Угол между заданными пересекающимися прямыми может быть найден через
угол между направляющими векторами этих прямых;
угол между нормальными векторами прямых;
угол между направляющим вектором одной прямой и нормальным вектором другой прямой.
Очевидно, если угол между векторами
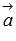 и
и 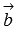 не
тупой, то он равен углу между пересекающимися
прямыми a и b.
Если же угол между направляющими
векторами прямых a иb тупой,
то угол между пересекающимися
прямыми a и b равен
углу, смежному с углом
не
тупой, то он равен углу между пересекающимися
прямыми a и b.
Если же угол между направляющими
векторами прямых a иb тупой,
то угол между пересекающимися
прямыми a и b равен
углу, смежному с углом 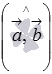 .
То есть,
.
То есть,  ,
если
,
если 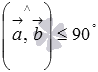 ,
а
,
а 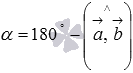 ,
если
,
если 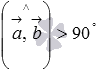 .
Так
как косинусы равных углов равны, то
последние равенства можно записать в
виде:
.
Так
как косинусы равных углов равны, то
последние равенства можно записать в
виде: 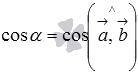 ,
если
,
а
,
если
,
а 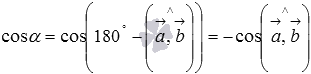 (в
последнем переходе мы использовали формулы
приведения),
если
.
Следовательно,
(в
последнем переходе мы использовали формулы
приведения),
если
.
Следовательно, 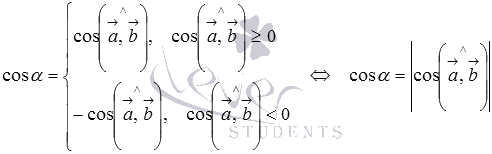 ,
то есть,косинус
угла между пересекающимися прямыми
равен модулю косинуса угла между
направляющими векторами пересекающихся
прямых.
,
то есть,косинус
угла между пересекающимися прямыми
равен модулю косинуса угла между
направляющими векторами пересекающихся
прямых.Формула для вычисления косинуса угла между векторами
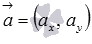 и
и 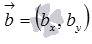 имеет
вид
имеет
вид 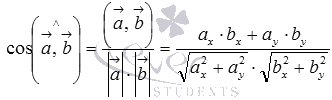 .
Тогда косинус
угла между двумя пересекающимися
прямыми a и b мы
можем найти по формуле
.
Тогда косинус
угла между двумя пересекающимися
прямыми a и b мы
можем найти по формуле 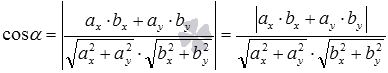 ,
а
сам угол
между пересекающимися прямыми -
по формуле
,
а
сам угол
между пересекающимися прямыми -
по формуле  ,
где
и
-
направляющие векторы прямых а и b соответственно.
,
где
и
-
направляющие векторы прямых а и b соответственно.Дадим еще формулу для нахождения угла между двумя пересекающимися прямыми a и b через угловые коэффициенты этих прямых.
Пусть прямую a на плоскости в заданной прямоугольной системе координат Oxy определяетуравнение прямой с угловым коэффициентом вида
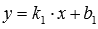 ,
а прямую b -
,
а прямую b - 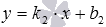 .
Тогда угол между пересекающимися
прямыми может быть вычислен по формуле
.
Тогда угол между пересекающимися
прямыми может быть вычислен по формуле 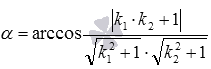 ,
где k1 и k2 –
угловые коэффициенты прямых a и bсоответственно.
Эту формулу легко получить на основании
формулы для определения угла между
пересекающимися прямыми через координаты
нормальных векторов прямых.
,
где k1 и k2 –
угловые коэффициенты прямых a и bсоответственно.
Эту формулу легко получить на основании
формулы для определения угла между
пересекающимися прямыми через координаты
нормальных векторов прямых.1. Нормальное уравнение прямой
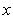
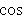
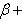
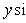
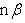
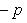
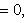
где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а
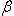 -
угол наклона этого перпендикуляра к
оси Ox.
Чтобы привести общее уравнение
прямой Ax + By + C =
0 к нормальному виду, нужно все члены
его умножить на нормирующий множитель
-
угол наклона этого перпендикуляра к
оси Ox.
Чтобы привести общее уравнение
прямой Ax + By + C =
0 к нормальному виду, нужно все члены
его умножить на нормирующий множитель 
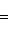
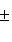
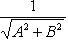 ,
взятый со знаком, противоположным знаку
свободного члена C.
,
взятый со знаком, противоположным знаку
свободного члена C.2. Расстояние точки A(x1, y1) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

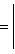
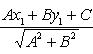

Правило. Чтобы определить расстояние точки A(x1, y1) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:
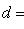
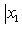
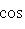
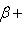

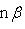
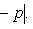
Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.
Отклонение
 данной
точки от данной прямой есть расстояние
от этой точки до прямой, которому
приписывается знак плюс, если точка и
начало координат находятся по разные
стороны от прямой, и знак минус, если
точка и начало координат находятся по
одну сторону от прямой.
данной
точки от данной прямой есть расстояние
от этой точки до прямой, которому
приписывается знак плюс, если точка и
начало координат находятся по разные
стороны от прямой, и знак минус, если
точка и начало координат находятся по
одну сторону от прямой.Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.
всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (3.2)
2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями:
![]() =
=![]() ;
(3.3)
;
(3.3)
3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
![]() .
(3.4)
.
(3.4)
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x1 +mt, y = y1 + nt, z = z1 + рt. (3.5)
Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекцияхили к приведенным уравнениям прямой:
x = mz + a, y = nz + b. (3.6)
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
![]() .
.
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
![]()
равносильна
системе ![]() ;
такая прямая перпендикулярна к оси Ох.
;
такая прямая перпендикулярна к оси Ох.
Система ![]() равносильна
системе x = x1, y
= y1;
прямая параллельна оси Oz.
равносильна
системе x = x1, y
= y1;
прямая параллельна оси Oz.
Билет№10
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
![]()
в
котором по крайней мере один из
коэффициентов ![]() отличен
от нуля.
отличен
от нуля.
Как
известно, уравнение окружности радиуса ![]() с
центром в точке
с
центром в точке ![]() имеет
вид:
имеет
вид:
![]() (3.1).
(3.1).
Если
в этом уравнении раскрыть скобки и
перенести ![]() в
левую часть равенства, то уравнение
примет вид:
в
левую часть равенства, то уравнение
примет вид:
![]() (3.1`).
(3.1`).
Геометрический
смысл уравнения не изменится, если все
его члены умножить на один и тот же,
отличный от нуля и не зависящий
от ![]() и
и ![]() множитель
множитель ![]() ;
введем обозначения –
;
введем обозначения – ![]() ,
–
,
– ![]() ,
, ![]() .
.
Уравнение (3.1') запишется тогда в виде:
![]() (3.2).
(3.2).
Возникает вопрос: всякое ли уравнение вида (3.2) является уравнением некоторой окружности?
Чтобы
ответить на этот вопрос, проделаем
обратное преобразование уравнения
(3.2) к виду (3.1), считая
коэффициенты A, D, E и F произвольными
(но ![]() ).
).
Разделим
все члены уравнения (3.2) на А и
введем обозначения: ![]() ,
, ![]() ,
, ![]() ;
тогда уравнение (3.2) примет вид:
;
тогда уравнение (3.2) примет вид:
![]() (3.2`).
(3.2`).
Дополняя
члены с x и y до
полных квадратов и перенося член ![]() направо,
придадим уравнению (3.2') вид:
направо,
придадим уравнению (3.2') вид:
![]() (3.3).
(3.3).
Правая часть последнего уравнения может быть числом положительным, отрицательным или нулем.
1.
Если ![]() ,
то положим
,
то положим ![]() .
.
Уравнение (3.3) запишется в виде:
(3.3`)
и является, как известно, уравнением окружности радиуса R с центром в точке .
2.
Если ![]() ,
то уравнение (3.3) принимает вид:
,
то уравнение (3.3) принимает вид:
![]() (3.3``).
(3.3``).
Ему
удовлетворяют только значения ![]() ,
, ![]() (сумма
двух квадратов может быть равна нулю
только тогда, когда одновременно равен
нулю каждый из них); таким образом,
уравнению (3.3'') удовлетворяет единственная
точка плоскости
.
Но, впрочем, можно говорить, что уравнение
(3.3'') и в этом случае является уравнением
окружности, но окружности, выродившейся
в точку (окружности с нулевым радиусом).
(сумма
двух квадратов может быть равна нулю
только тогда, когда одновременно равен
нулю каждый из них); таким образом,
уравнению (3.3'') удовлетворяет единственная
точка плоскости
.
Но, впрочем, можно говорить, что уравнение
(3.3'') и в этом случае является уравнением
окружности, но окружности, выродившейся
в точку (окружности с нулевым радиусом).
3.
Если ![]() ,
то полагая
,
то полагая ![]() ,
приводим уравнение (3.3) к виду:
,
приводим уравнение (3.3) к виду:
![]() (3.3```).
(3.3```).
Поскольку сумма квадратов двух вещественных чисел не может быть числом отрицательным, то на плоскости xOy не существует точек, которые удовлетворяли бы уравнению (3.3'''). Поэтому уравнение (3.3''') не определяет никакой кривой; иногда говорят, впрочем, что уравнение (3.3''') является уравнением мнимой окружности.
Только учитывая это последнее замечание, можно говорить, что уравнение (3.2) всегда определяет окружность (вещественную, выродившуюся в точку или мнимую).
Билет№11
Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).
Простейшее уравнение эллипса
![]()
![]()
![]()
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение
a2 - b2 = c2.
Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси
![]()
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
![]()
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
Соотношения
Билет№12
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.
Простейшее уравнение гиперболы
![]()
![]()
![]()
Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.
Если 2c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение
a2 + b2 = c2.
При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид
x2 - y2 = a2.
Фокусы гиперболы лежат на ее действительной оси.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.
![]()
Асимптоты гиперболы - две прямые, определяемые уравнениями
![]()
![]()
Напомним, что асимптотой кривой, имеющей бесконечную ветвь, называется прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
Вид кривой |
Каноническое уравнение |
Инварианты |
Невырожденные
кривые ( |
||
Эллипс |
|
|
Гипербола |
|
|
Парабола |
|
|
Вырожденные
кривые ( |
||
Точка |
|
|
Две пересекающиеся прямые |
|
|
Две параллельные прямые |
|
|
Одна прямая |
|
|
Билет№13