Билет №1

Вектором называется направленный отрезок. Если у отрезка AB его концы равноправны, то для вектора один из концов отрезка, например, A называется началом, а другой, то есть B, – концом. Обозначим вектор либо указанием концов отрезка, причем начало вектора ставится на первое место, либо строчной латинской буквой со стрелкой или чертой над буквами. Векторы   и   называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены. Если лучи AB и CD противоположно направлены, векторы   и   называются противоположно направленными. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора   обозначим   Два вектора называютсяравными, если они одинаково направлены и равны по абсолютной величине. Углом между ненулевыми векторами   и   называется угол BAC. Углом между любыми двумя ненулевыми векторами   и   называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами равен нулю.

Нулевым вектором   называется вектор, у которого начало совпадает с концом. Направление нулевого вектора не определено, а его модуль считается равным нулю. Вектор называется единичным, если его абсолютная величина равна единице.

Замечание 11.1

Любую пару векторов, один из которых равен нулевому вектору будем считать коллинеарными.

Т еорема 11.1. 

Два вектора, сонаправленные с третьим вектором, сонаправлены.

Доказательство

Свойства равенства векторов:

• каждый вектор равен самому себе;

• если вектор   равен вектору 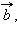  то   равен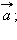 

• два вектора, равные третьему, равны.

Т еорема 11.2. 

Пусть даны два вектора   и   не лежащие на одной прямой. Соединим начала A и C и концы B и D этих векторов. Если четырехугольник ABDC – параллелограмм, то   и наоборот, если   то четырехугольник ABDC – параллелограмм.

Свойства операции сложения:

1°      - коммутативность

2°      - ассоциативность

3°    

4°    

Разностью   векторов   и   называется вектор   такой, что выполняется условие:  .

Произведением   вектора   на число   называется вектор  , удовлетворяющий условиям:

1. 

2. 

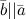
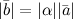
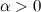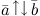3. , если  ,  , если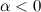 

Свойства умножения вектора на число:

1°    

2°    

3°    

4°    

5°    

6°    

Скалярное произведение векторов обозначается точкой   и является скаляром, т.е. величиной, каждое значение которой может быть выражено числом. Скалярами, например, являются масса, температура, давление, длина и т.д.

Скалярным произведением двух ненулевых векторов   и   называется число, равное произведению длин этих векторов на косинус угла между ними:

Свойства скалярного произведения:

1°      - симметричность.

2°     . Обозначается   и называется скалярный квадрат.

3°    Если  , то 

4°    Если   и   и  , то  . Верно и обратное утверждение.

5°    

6°    

7°    

Векторным произведением ненулевых векторов   и   называется вектор  , обозначаемый символом   или  , длина которого  .

Свойства векторного произведения:

1°     , тогда и только тогда, когда 

2°    

3°    Модуль векторного произведения   равен площади параллелограмма, построенного на заданных векторах   и  (рис. 2), т.е.

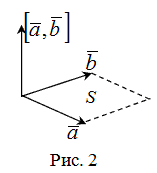
4°    

5°    

Определение

Смешанным произведением трех векторов  ,  ,   называется число, равное скалярному произведениювектора   на вектор  : 

Свойства смешанного произведения:

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Имеют место следующие две основные теоремы о проекциях векторов:

1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:

2). При умножении вектора на число его проекция умножается на то же число:

.

В частности, если

,  ,

то

,

и

.

Если  , то для любого числа 

.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов

,  ,

является пропорциональность их координат:

.

Тройка векторов  ,  ,   называется координатным базисом, если эти векторы удовлетворяют следующим условиям:

1). Вектор   лежит на оси Ох, вектор   - на оси Оу, вектор   - на оси Oz;

2). Каждый из векторов  ,  ,   направлен по своей оси в положительную сторону;

3). Векторы  ,  ,   единичные, то есть  ,  ,  .

Каким бы ни был вектор  , он всегда может быть разложен по базису  ,  ,   , то есть может быть представлен в виде

;

коэффициенты этого разложения являются координатами вектора   (то есть X, Y, Z суть проекции вектора   на координатные оси).

Билет №2 Линейная зависимость векторов

Введем еще одно очень важное понятие, которое используется не только в алгебре, но и во многих других разделах математики.

        Определение 10.14   Система векторов   называется линейно зависимой, если существует такой набор коэффициентов   , из которых хотя бы один отличен от нуля, что   .         

Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по другому.

        Определение 10.15   Система векторов   называется линейно независимой, если равенство   возможно только при   .         

Кто плохо понял два последних определения, может получить дополнительные объяснения здесь.

        Предложение 10.6   Система векторов   линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

        Доказательство.     Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов   , что   , причем хотя бы один коэффициент отличен от нуля. Предположим, что   . Тогда

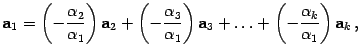
то есть   является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор   , то есть   . Очевидно, что   . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен   ).      

        Предложение 10.7   Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

        Доказательство.    

Пусть в системе векторов   подсистема   ,   , является линейно зависимой, то есть   , и хотя бы один коэффициент отличен от нуля. Тогда составим линейную комбинацию   . Очевидно, что эта линейная комбинация равна нулю, и что среди коэффициентов есть ненулевой.      

Упражнение10.4.1. Докажите, что если система векторов линейно независимая, то любая ее подсистема линейно независимая.     

        Предложение 10.8   Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

        Доказательство.     Пусть система состоит из вектора   . Линейная комбинация имеет вид   . Если   , то   , то есть система линейно зависима. Если   и   , то   .      

        Предложение 10.9   Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

        

Доказательство этого предложения предоставляется читателю. Оно аналогично доказательству следующего предложения.

        Предложение 10.10   Система из трех векторов линейно зависима тогда и только тогда, когда эти векторы компланарны.

        Доказательство.     Пусть векторы    -- компланарные. Если    -- коллинеарные, то в силу предыдущего предложения они образуют линейно зависимую подсистему системы   . По  предложению 10.7 система    -- линейно зависима. Если векторы   -- неколлинеарные, то по  предложению 10.2   является линейной комбинацией векторов   и по  предложению 10.6 система векторов    -- линейно зависимая.

Пусть система векторов линейно зависима. По  предложению 10.6 один вектор, скажем   , является линейной комбинацией других векторов,   и   ,   . Правая часть последнего равенства лежит в плоскости, в которой лежат векторы   . Поэтому вектор   лежит в одной плоскости с векторами   , то есть векторы    -- компланарные.      

        Предложение 10.11   Четыре вектора всегда образуют линейно зависимую систему.

        Доказательство.     Если первые три вектора являются компланарными, то они образуют линейно зависимую подсистему ( предложение 10.10). Следовательно, вся система линейно зависима ( предложение 10.7). Если первые три вектора -- некомпланарные, то четвертый является их линейной комбинацией ( предложение 10.3). По  предложению 10.6 система является линейно зависимой.      

На основании сказанного дадим другое определение базиса, которое является более распространенным, чем  определение 10.12.

        Определение 10.16   Базисом векторного пространства   называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства   раскладывается по векторам этой системы.         

Из  предложений 10.8 – 10.11 следует, что это определение эквивалентно определению 10.12.

Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «анти параллельными»). Свойства коллинеарности

Пусть   — векторы пространства  . Тогда верны следующие утверждения:

• Коллинеарность — отношение эквивалентности, то есть оно:

  1. рефлексивно: 

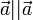
  2. симметрично: 

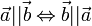
  3. транзитивно: 

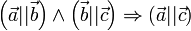
• Нулевой вектор коллинеарен любому вектору: 

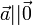
• Скалярное произведение коллинеарных векторов 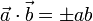  равно произведению длин векторов (взятых со знаком «-», если векторы противоположно направлены)

• Векторы на плоскости коллинеарны тогда и только тогда, когда их псевдоскалярное произведение равно 0.

• Коллинеарные векторы линейно зависимы.

• Существует действительное число 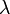  такое, что 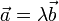  для коллинеарных 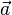  и 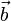 , за исключением особого случая 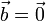 . Это определения и также критерий коллинеарности.

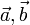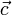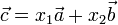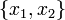• На плоскости 2 неколлинеарных вектора   образуют базис. Это значит, что любой вектор   можно представить в виде:  . Тогда   будут координатами  в данном базисе.