2.1.6 Подсчет частот (частостей) попадания случайных величин в интервалы группирования.

Вычисляются границы каждого из К интервалов. Подсчитывается количество п_j, данных, находящихся в каждом из интервалов и вычисляются частости р_j, попадания в каждый интервал

₍₂₂₎

Необходимо следить, чтобы в каждый интервал попадало не менее пяти данных, в противном случае интервал объединяется с соседним интервалом таким образом, чтобы ожидаемое число наблюдений в обеденном интервале было не менее пяти.

Построение гистограммы

Для графического изображения эмпирического распределения по швы граничным точкам или серединам интервалов строится график – гистограмм, вид которой представлен на рисунке 4.

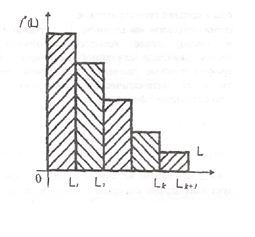
Рисунок 4 – Гистограмма

Для построения гистограммы по оси абсцисс откладываются в выбранном масштабе интервалы, и, взяв их как основания, строят прямоугольники, площадь которых равна частости попадания случайной в интервал. Частость каждого интервала делится на его ширину, число берется как высота прямоугольника. Построенная таким образом ступенчатая функция fэ,(L) называется гистограммой выборки. Эта функция служит статистическим аналогом плотности распределения вероятности случайной величины и определяется как

f_э(L)=n_j/∆L n=p_j/∆L. (23)

Площадь гистограммы равна единице.

2.2 Статистические меры случайных распределений

Числовыми характеристиками случайной величины называются характеристики наиболее существенных особенностей распределения -центра распределения, масштаба и формы кривой распределения, которые служат для описания и сравнения распределений.

Наиболее часто используемыми в теории надежности числовыми характеристиками случайной величины являются характеристики положения:

-математическое ожидание (среднее арифметическое);

-медиана или срединное значение;

-мода и среднее геометрическое.

Математическим ожиданием L случайной величины называется постоянное число, около которого устойчиво колеблется среднее арифметическое значение случайной величины. При большой выборке среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию, которое может быть вычислено по следующей формуле:

(24)

Модой Д случайной величины является такое ее значение, которому соответствует наибольшее значение плотности распределения Д = p_mчi. Как и медиана, мода не подвержена воздействию крайних членов ряда измерений; она зависит лишь от соотношения величин в «точке накопления». Нормальное распределение одномодально, для него мода и математическое ожидание совпадают.

Мода удобна для исследования многовершинных распределений.

Важной числовой характеристикой распределения при малых выборках (от пяти до девяти значений), является медиана или срединное значение. Если п - нечетное число, то медиана просто является числом, расположенным в середине упорядоченной последовательности. Если п -четное число, то медиана - это среднее арифметическое двух рядом стоящих срединных значений,

У нормального распределения медиана совпадает с математическим ожиданием и модой.

Среднее геометрическое ряда измерений L

₍₂₅₎

На практике среднее геометрическое используется для исследования динамики фактора, например, среднего темпа возрастания (снижения) брака. Основные числовые характеристики положения показаны на рисунке 5.

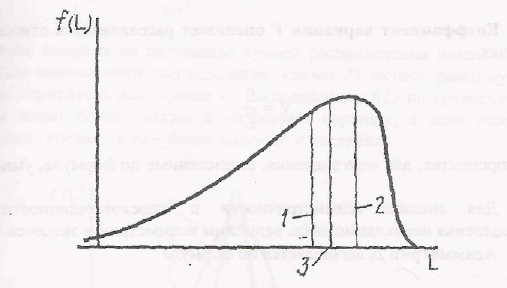
1- медиана, 2 - мода, 3 - математическое ожидание

Рисунок 5 -Плотность вероятности и числовые характеристики положения случайной величины

Характеристики рассеяния - дисперсия, среднее квадратическое отклонение и коэффициент вариации случайной величины - показывают, насколько тесно сгруппированы возможные значения случайной величины около ее математического ожидания, т.е. характеризуют степень разброса рассеивания.

Дисперсией D случайной величины называется математическое - ожидание квадрата отклонения случайной величины от ее математического ожидания

(26)

Чем меньше дисперсия, тем большая доля значений случайной величины примыкает к ее математическому ожиданию, и наоборот, - чем больше дисперсия, тем большая доля значений случайной величины удалена от математического ожидания.

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому часто на практике используется характеристика,

размерность которой совпадает с размерностью случайной величины - среднее квадратическое отклонение S, которое разно квадратному корню из дисперсии, взятому с положительным знаком:

₍₂₇₎

Коэффициент вариации V оценивает рассеивание в относительных единицах

₍₂₈₎

или в процентах, для чего значения, вычисленные по формуле, умножают на 100.

Для анализа асимметричности и плосковершинности кривой распределения необходимо знать величины асимметрии и эксцесса.

Асимметрия р_ь вычисляется по формуле

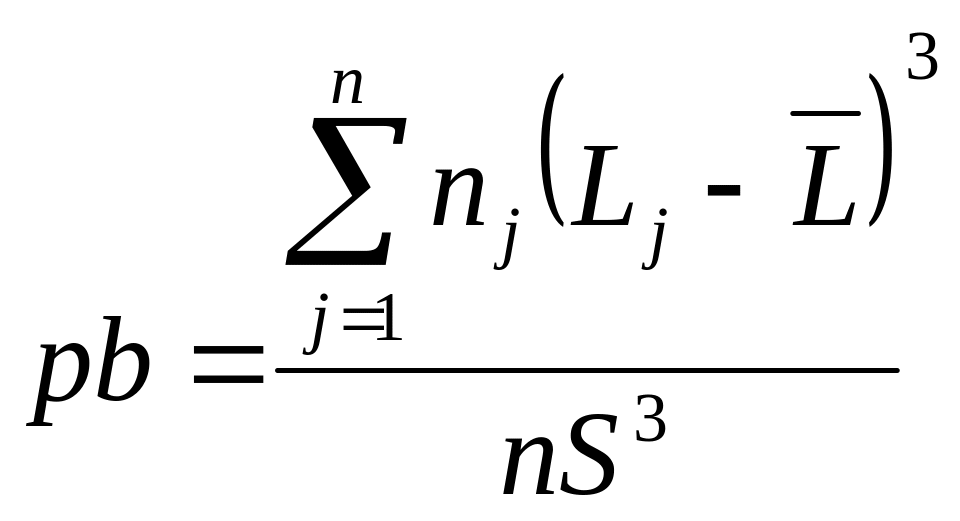(29)

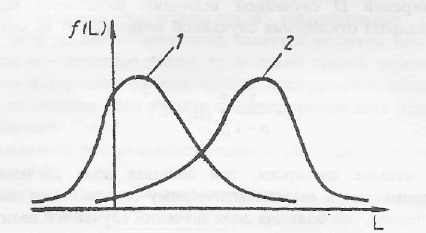
Рисунок 6 –Влияние ассиметрии на положение кривой распределения

Если кривая распределения симметрична, то асимметрия равна нулю; если вытянутая часть кривой расположена слева от моды, то асимметрия отрицательна, а если справа - положительна. На рисунке 6 показаны два асимметричных распределения, из которых 1 имеет положительную, а 2 -отрицательную асимметрию.

Эксцесс E_k характеризует плосковершинность кривой распределения

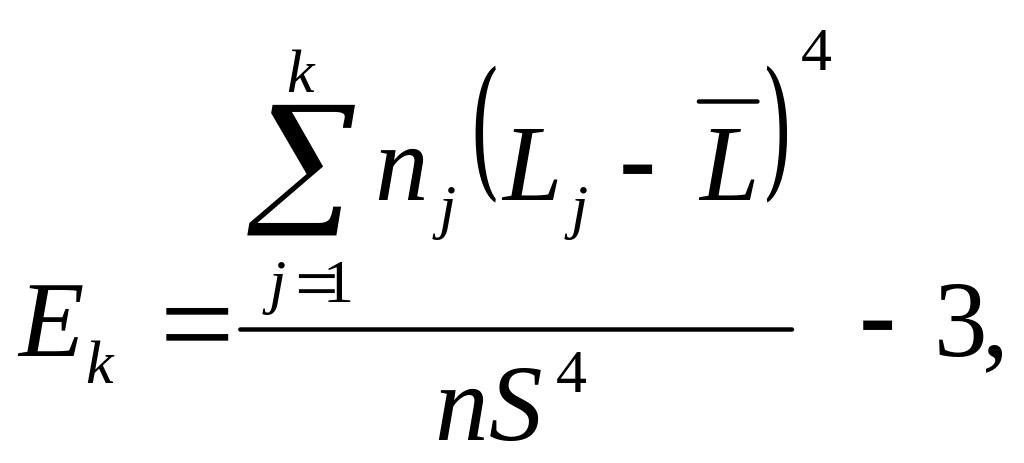
(30)

Влияние эксцесса на положение кривой распределения показано на рисунке 7. Для нормального распределения (кривая 3) эксцесс равен нулю. Не ли эксцесс отрицательный (кривая 4), распределение f(L) по сравнению с нормальным имеет более низкую и «плоскую» вершину, а если эксцесс положительный (кривая 5), то - более высокую и «острую».

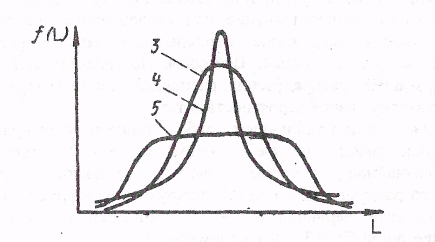
Рисунок 7 - Влияние эксцесса на положение кривой распределения