3.4 Расчет схемной надежности сложных систем

При расчете обычно требуется определить вероятность безотказной работы P(t) всей системы.

Наиболее характерен случай, когда отказ одного элемента выводит из строя всю систему, как это имеет место при последовательном соединении элементов, схема которого представлена на рисунке 13. Например, большинство приводов машин и механизмы передач подчиняются этому условию. Так, если в приводе машины выйдет из строя любая шестерня, подшипник, муфта и т.д., то весь привод перестанет функционировать. При этом отдельные элементы не обязательно должны быть соединены последовательно. Например, подшипники на валу редуктора работают конструктивно параллельно друг с другом, однако выход из строя любого из них приводит к отказу системы.

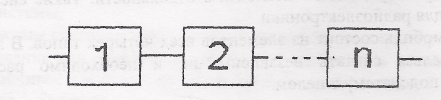
Рисунок 13 – Последовательное соединение элементов

В системе с последовательным соединением для безотказной работы в течении некоторой наработки t необходимо и достаточно, чтобы каждый из ее n элементов работал безотказно в течении этой наработки.

Расчет надежности таких систем основан на допущении о том, что все распределения наработки до отказа и времени восстановления отдельных элементов являются экспоненциальными, то есть процесс функционирования систем является стационарным, без последствия и ординарным.

Стационарность процесса означает постоянство параметра потока отказов в течении заданного промежутка времени.

Отсутствие последействия означает независимость появления отказов элементов системы, то есть отказы элементов системы взаимно независимы и не влияют друг на друга.

Ординарность процесса означает практическую невозможность появления двух или более отказов в одно и то же время. Принятое допущение справедливо, если средняя наработка до отказа элементов системы значительно больше времени их восстановления. На практике это условие обычно выполняется.

Считая отказы элементов независимыми, вероятность одновременной безотказной работы n элементов определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий

При одинаковой надежности элементов эта формула принимает вид

P(t)= . (68)

Сложные системы, состоящие из элементов с достаточно высокой надежностью, могут иметь общую низкую надежность из-за большого количества элементов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет , то вероятность безотказной работы узла будет

Если же узел состоит из 400 деталей с аналогичной безотказностью, то P(t)=0,018, то есть система практически неработоспособна.

Высокий уровень надежности систем с последовательным соединением элементов достигается в результате использования надежных элементов, правильно назначения периодичности технического обслуживания, обеспечения быстрого восстановления или замены отказавших элементов в процессе эксплуатации.

При параллельном соединении элементов, схема которого представлена на рисунке 14, отказ любого элемента не приводит к отказу системы, пока не откажут все соединенные элементы.

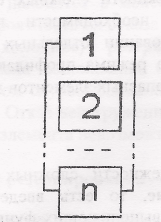
Рис 14 – Параллельное соединение элементов

Для отказа системы с параллельным соединением элементов в течение наработки t необходимо и достаточно, чтобы все ее элементы отказали в течении этой наработки. Так что отказ системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:

Соответственно, вероятность безотказной работы

(70)

Для систем из равнонадежных элементов ( = )

, (71)

, (72)

т.е. надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при p=0,9 и n=2 P=0,99, а при n=3 P=0,999)

В зависимости от поставленной задачи на основании результатов расчета характеристик надежности сложных систем делаются выводы и принимаются решения о необходимости изменения или доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.