2.3.3 Распределение Вейбулла

Распределение Вейбулла хорошо описывает распределения:

предела текучести ряда металлов;

характеристик прочности металлов;

-наработок до отказа многих невосстанавливаемых изделий например, подшипников качения;

-наработок между отказами сложных систем в процессе эксплуатации.

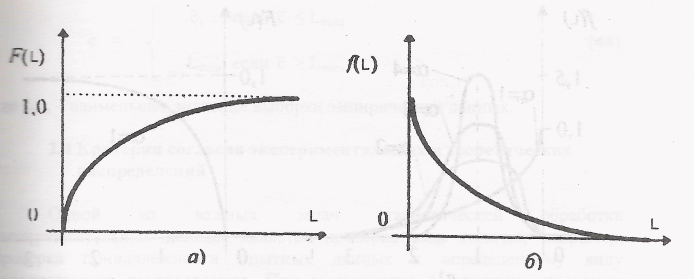
Рисунок 9 - Кривые функции (а) и плотности (б) экспоненциального распределения

Плотность распределения Вейбулла имеет вид

(40)

где а – параметр масштаба,

b – параметр формы,

с – параметр сдвига.

Интегральная функция распределения записывается в виде

(41)

Закон распределения Вейбулла является двухпараметрическим, а также универсальным, так как при определенных значениях параметров он может превращаться в экспоненциальное (при b = 1), нормальное (при b =3.3) другие распределения. Кривые плотностей и функции распределения приведенные на рисунке 10.

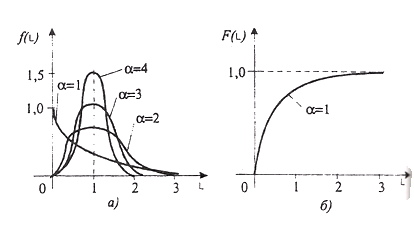
Рисунок 10 - Кривые плотностей (а) и функции (б)

распределения Вейбулла

Определение оценок параметров а, Ь, с осуществляется методом моментов, сущность которого состоит в том, что параметры функции распределения могут быть выражены через начальные и центральные моменты. По эмпирическим данным вычисляются моменты, которые затем приравниваются к теоретическим. В конечном счете решается система уравнений, связывающая параметры с моментами, и определяются оценки соответствующих параметров.

Определение оценок параметров распределения Вейбулла по совокупности статистических данных осуществляется в следующей последовательности.

По полученному значению асимметрии p_b из специально составленной таблицы находят оценку параметра формы и значения коэффициентов g_b и k_b.

Определяют оценку параметра масштаба по формуле

= /g_b (42)

= - K_b (43)

В качестве оценки параметра с принимают одно из двух значений:

(44)

где L_min – наименьшее значение выборки эмпирических данных.

2.4 Критерии согласия экспериментальных и теоретических распределений

Одной из важных статистической обработки экспериментальных данных является проверка ряда гипотез, например, проверка принадлежности опытных данных к определенному виду

теоретического распределения. При выдвижении и принятии указанных гипотезе могут иметь место следующие четыре случая:

а) гипотеза верна и принимается;

б) гипотеза верна, но ошибочно отвергается. Возникающую при этом ошибку называют ошибкой первого рода, а вероятность ее появления называют уровнем значимости и обозначают а;

в) гипотеза неверна и отвергается;

г) гипотеза неверна, но ошибочно принимается. Возникающую при этом ошибку называют ошибкой второго рода, а вероятность ее появления обозначают β. Величину 1 - β, то есть вероятность того, что гипотеза будет отвергнута, когда она ошибочна, называют мощностью критерия.

Разработано множество критериев для проверки гипотез. Некоторые из них справедливы лишь для определенных распределений, другие справедливы для широкого круга распределений. Наиболее универсальными считаются критерии Пирсона, Колмогорова, Романовского, Стьюдента и др. для которых при заданном уровне значимости а подсчитаны и составлены таблицы критических значений.

При этом область возможных значений каждого из критериев делят на две части, как это показано на рисунке 11:

область принятия гипотезы,

область непринятия гипотезы (так называемая критическая область), которая для различных критериев может быть левосторонней или

правосторонней.

Порядок проверки статистических гипотез можно сформулировать так: если опытное значение критерия k_опытн вычисляемое при заданном уровне значимости а попадает в область принятия гипотезы, то гипотеза принимают. Если же опытное значение критерия попадает в критическую область, то гипотезу отвергают

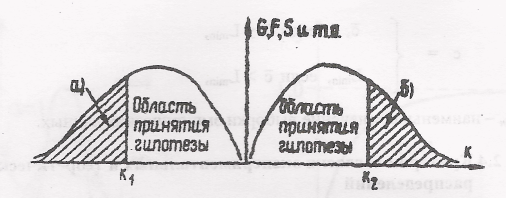
К₁ и К₂ – критические точки (табличные значения критериев)

Рисунок 11 – Левосторонняя (а) и правосторонняя (б) критические области

Уровню значимость соответствует доверительная вероятность =1- . При решении задач надежности автомобильно-дорожных средств принимается равной 0,95 и, следовательно уровень значимости принимается равным =0,05.

Рассмотрим наиболее широко распространенные критерии статистической оценки гипотез.