2.3 Законы распределения случайных величин

Статистические характеристики, полученные по опытным данным, еще не позволяют анализировать характер изменения случайной величины. Необходимо знать закон ее распределения, выраженный в математической форме - интегральную функцию распределения или функцию плотности распределения вероятностей.

Плотность распределения f(L) подчиняется соотношению

где F(L) - функция распределения:

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Законы распределения имеют большое значение для теории и практики обеспечения надежности объекта. Они позволяют:

- выполнить контроль уровня надежности в эксплуатационных условиях;

- выявить возможности дальнейшего увеличения ресурса;

определить необходимость выполнения работ по совершенствованию конструкций и по повышению уровней их надежности.

Наибольшее распространение для исследования эксплуатационной надежности имеют следующие непрерывные законы распределения: нормальный, экспоненциальный, Вейбулла, логарифмически нормальный законы, гамма- и бета-распределения, распределения хи-квадрат, Стьюдента (Госсета), по закону равной вероятности и т.д.

Решение задачи о наилучшем подборе теоретического распределения s общем случае является неопределенным, поэтому для принятия модели описания случайной величины часто учитывают внешний вид эмпирического распределения или анализируют характеристики. Например, при коэффициенте вариации V = 1 принимается экспоненциальное распределение, а при V< 0,3 ...0,4 - нормальное.

Рассмотрим наиболее распространенные непрерывные

распределения.

2.3.1 Нормальное распределение (закон Гаусса)

Нормальное распределение наиболее часто используется в задачах надежности для описания изменения случайной величины, на которое оказывают влияние многие примерно разнозначные факторы, например:

-постепенных отказов;

-суммарной наработки ряда восстанавливаемых изделий до капитального ремонта;

-наработки до отказа не восстанавливаемых изделий;

времени восстановления ремонтируемых изделий. Плотность нормального распределения определяется выражением

(33)

Интегральная функция нормального распределения

(34)

Кривые функции и плотности нормального распределения приведены на рисунке 8.

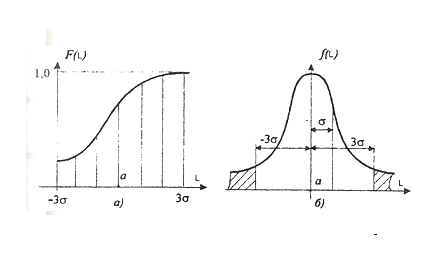
Рисунок 8 - Кривые функции (а) и плотности (б) нормального распределения

Распределение имеет два независимых параметра - математическое ожидание и среднее квадратическое отклонение.

Совокупность всех значений случайной величины, подчиненной нормальному закону, практически с вероятностью 99,73% попадает в область, ограниченную интервалом -3S слева и 3S справа от среднего значения.

2.3.2 Экспоненциальное (показательное) распределение

Экспоненциальное распределение используется при рассмотрении:

- внезапных отказов в тех случаях, когда явления изнашивания и старения настолько слабо выражены, что ими можно пренебречь, например, радиоэлектронной аппаратуры;

- наработок между отказами восстанавливаемых изделий после окончания периода приработки;

- в первом приближении - времени восстановления ремонтируемых изделий.

Распределение используется в проектных расчетах надежности на стадии разработки сложных систем и его часто называют основным законом надежности. Особенность этого закона - простота в практическом применении и отсутствие больших вычислительных процедур при расчете надежности.

Плотность экспоненциального распределения выражается соотношением (для L>0)

f(L)=λexp(-λL), (35)

где λ - параметр распределения, имеющий вероятностный смысл.

Интегральная функция этого распределения находится по уравнению

F(L)=1-exp(-λL) (36)

Математическое ожидание и дисперсия связаны с параметром, распределения следующими соотношениями:

=1/λ (37)

D=1/λ² (38)

Коэффициент вариации для экспоненциального распределения определяется как

V=S/ =1. (39)

Распределение является однопараметричеким, так как характер изменения кривой зависит от одного параметра Кривые функции плотности распределения показаны на рисунке 9.