Лекции по квантовой механике_1 / Lekciya17

Лекция 17

Спин элементарных частиц. Спиновые волновые функции и операторы спина

Рассмотрим составную частицу, состоящую из двух элементарных частиц и совершающую некоторое пространственное движение (примером такой составной частицы может быть ядро дейтерия, состоящее из нейтрона и протона). Состояния такой частицы могут быть описаны с помощью волновой функции, зависящей от ее координаты как целого, например, координаты центра инерции , и координаты относительного движения . Такая волновая функция определяет вероятности различных положений частицы как целого и относительного положения ее составных частей. Физическим величинам, определяемым «внутренними» переменными, отвечают операторы, действующие на координату , величинам, связанным с движением частицы как целого, - операторы, действующие на радиус-вектор центра инерции. В частности, моменту импульса относительного движения составных частей отвечают операторы , , и , действующие на относительную переменную и обладающие всеми свойствами операторов момента, которые рассматривались ранее. В частности, квадрат момента относительного движения может иметь определенное значение вместе с одной из проекций (например, с ). Проекции «внутреннего» момента одновременно определенных значений, вообще говоря, не имеют. Общими собственными функциями операторов квадрата момента импульса «внутреннего» движения и его проекции на ось являются сферические функции , зависящие от углов и относительного радиуса-вектора, при этом индекс определяет величину «внутреннего» момента импульса частицы, индекс - его проекцию на ось , то есть ориентацию вектора момента в пространстве. Квантовые числа и могут принимать следующие значения: , при фиксированном квантовое число может принимать дискретный ряд значений от до через единицу.

Рассмотрим теперь такое состояние составной частицы, когда энергия и момент внутреннего движения фиксированы, и будем интересоваться только величинами, относящимся к движению частицы как целого. С одной стороны, при таком описании нам нужна только та часть волновой функции, которая связана с «внешним» движением. Однако с другой стороны есть одна характеристика «внутреннего» движения, которая не фиксируется фиксацией внутреннего состояния частицы - это проекция внутреннего момента на любую выделенную ось. Эта проекция может меняться при фиксированном внутреннем состоянии составной частицы, и, следовательно, при описании «внешнего» движения необходимо учесть возможность изменения этой проекции. Это значит, что та часть волновой функции составной частицы, которая описывает «внешнее» движение должна содержать еще одну дискретную переменную - проекцию внутреннего момента на выделенную ось и определять вероятность того, что частица находится в той или иной точке пространства и имеет то или иное значение проекции внутреннего момента на выделенную ось.

Таким образом при описании движения составной частицы как целого в случае, когда не меняется ее «внутреннее» состояние, квантовая механика формально допускает введение дополнительной дискретной координаты, характеризующей внутренние степени свободы. Поэтому нельзя a priori отвергнуть существование такой координаты для элементарных частиц только на основе их «элементарности».

Как показывает опыт, элементарные частицы кроме момента импульса, связанного с движением в пространстве (и который в этом контексте называют «орбитальным»), могут обладать и «внутренним» моментом импульса, который не зависит от их пространственного движения. Этот момент называется спином частицы. Величина «внутреннего» момента (или спина) - такая же характеристика любой элементарной частицы, как ее масса или заряд, и которая независимо от состояния этой частицы всегда имеет определенное значение. Проекция же вектора спина на некоторую ось может в тех или иных случаях принимать различные значения, а также может меняться при действии на частицу тех или иных полей.

Как и всякой векторной физической величине спину соответствует некоторый оператор , имеющий три компоненты, причем можно предположить, что для операторов, отвечающих проекциям спина, справедливы те же коммутационные соотношения, что и для операторов проекций орбитального момента импульса (здесь и далее в этой главе )

, а также (1)

Такие коммутационные соотношения можно ожидать из следующих соображений. Мы установили (когда рассматривали момент импульса), что волновая функция при повороте системы координат преобразуется следующим образом:

(*)

причем для проекций оператора на координатные оси справедливо соотношение (*). Поэтому и здесь мы должны допустить справедливость соотношений (1).

Из соотношений (1) следует, что оператор квадрата спина имеет общие собственные функции с одним из операторов проекций, в то время как операторы проекций спина общих собственных функций не имеют. Коммутационные соотношения (1) позволяют найти все собственные значения операторов , , и . А именно, собственные значения оператора квадрата спина могут быть записаны в виде , где - неотрицательное целое или «полуцелое» число (т.е. число вида 0, 1/2, 1, 3/2, 2, 5/2 ...). Собственные значения оператора проекции спина на любую ось для частицы со спином равны , , ..., .

Как отмечено выше, существование спина у частиц приводит к тому, что в число аргументов волновой функции необходимо ввести дискретную «спиновую координату» , которая принимает значения, равные различным возможным значениям проекции спина на ось . Поскольку спиновая координата дискретна, то вместо введения спиновой координаты в список аргументов волновой функции, ее можно записывать в виде индекса, или записывать волновую функцию частицы со спином в виде столбца, содержащего компонент

(2)

договорившись, что квадрат модуля верхней компоненты определяет вероятность того, что частица находится в точке с координатами и имеет проекцию спина на ось , равную (максимальное значение), квадрат модуля второй компоненты определяет вероятность того, что частица находится в точке с координатами и имеет проекцию спина на ось , равную (второе по величине значение) и так далее. Из определения волновой функции частицы со спином следует, что величина

(3)

определяет вероятность того, что частица имеет проекцию спина на ось , равную независимо от ее положения в пространстве, а величина определяет вероятность того, что частица находится в точке с координатами независимо от проекции спина. Естественным образом модифицируются при наличии спина скалярное произведение волновых функций

(4)

и условие нормировки волновой функции

(5)

которое выражает то обстоятельство, что сумма вероятностей всех возможных несовместных событий, происходящих с частицей, равна единице.

В квантовой механике часто приходится рассматривать такие состояния, когда вероятности различных значений проекций спина не зависят от координат. В этом случае пространственные и спиновые переменные в волновой функции разделяются (это обстоятельство является отражением теоремы умножения вероятностей независимых событий) и волновая функция имеет вид

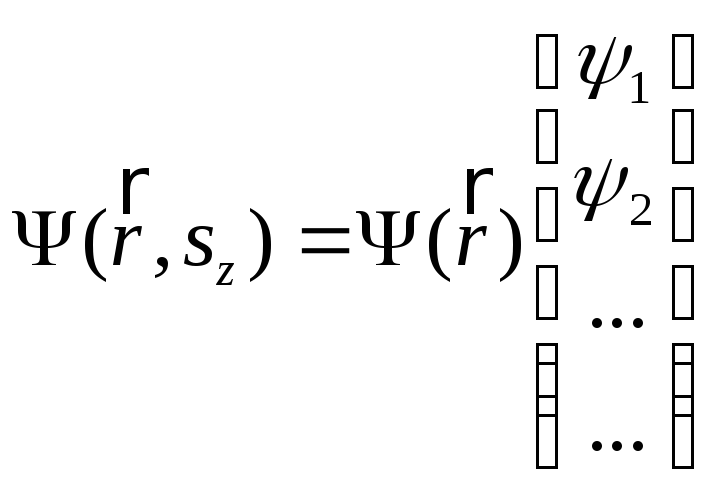(6)

где , ,... - числа. В этом случае о волновой функции говорят как о пространственной части волновой функции, а столбец из чисел , ,... определяющих вероятности различных значений проекции спина на ось , называют спиновой частью волновой функции (или просто спиновой волновой функцией, или спинором).

В случае частиц со спином квантовомеханические операторы физических величин должны связывать друг с другом различные функции вида (6). При этом, поскольку спин никак не связан с пространственным положением частицы, операторы спина должны связывать различные спиновые функции (то есть «действовать» на спиновую функцию) и никак не затрагивать функции, зависящие от пространственных переменных (не «действовать» на функции пространственных координат). Поэтому в общем виде результат действия такого оператора можно записать как произведение некоторой матрицы на спинор

(7)

где - некоторые числа, являющиеся характеристикой данного оператора. Таким образом, каждому оператору, действующему на спиновую функцию, соответствует некоторая матрица из чисел . Матрицу любого спинового оператора можно найти, если известен результат действия этого оператора на базисные функции:

(8)

Матрицы операторов спина можно найти из следующих соображений.

Работаем в базисе собственных функций операторов и . Тогда матрицы оператора диагональная:

(**)

Далее, из коммутационных соотношений (1) следует, что операторы - повышающий и понижающий:

(***)

Поэтому у ненулевыми являются только наддиагональные элементы, а у - только поддиагональные.

Константы в (***) можно найти так. Найдем матрицы операторов. имеет диагональную матрицу, значит,

т.к. есть комплексно сопряженное к отсюда:

Из этого соотношения мы определяем только модули матричных элементов. Фазы выбираются произвольно. Мы выбрали фазы так, чтобы у матричных элементов фазы были нулевыми, и они были действительны.

А затем через матрицы операторов операторы можно найти У операторов :

Вместе с они составляют полный набор матриц оператора спина.

Построим матрицы спиновых операторов для частицы со спином ½. Выберем в качестве базисных функций спиноры

(9)

Очевидно, искомые матрицы представляют собой матрицы размерности . Начнем с построения матрицы оператора . Очевидно, в базисных состояниях проекция спина частицы на ось имеет определенное значение - в первом состоянии и во втором. Это связано с тем, что согласно определению спиновой функции вероятность обнаружить проекцию спина в первом состоянии равна 1, во втором 0, и наоборот для проекции . Следовательно, функции (9) являются собственными функциями оператора , отвечающими соответствующим собственным значениям первая, и вторая. Поэтому для матрицы оператора выполнены условия

(10)

Из формул (10) находим

(11)

Для построения матриц операторов и найдем сначала матрицы операторов . Поскольку коммутационные соотношения между операторами проекций спина такие же, как для операторов орбитального момента, то при действии операторов на собственные функции оператора получаются также собственные функции этого оператора, отвечающие на единицу большему или меньшему собственному значению. При действии операторов () на собственную функцию, отвечающую максимальному (минимальному) собственному значению получается спиновая функция, тождественно равная нулю, то есть нулевой столбец. Поэтому

(12)

Из соотношений (12) найдем, что

(13)

Из (13) и определения операторов находим

(14)

Матрицы операторов , и (11), (14) (без множителей 1/2) называются матрицами Паули и обозначаются , и .

Матрицу оператора легко найти, возводя в квадрат и складывая матрицы операторов проекций момента (11), (14)

(15)

Матрицу (15) можно было бы получить и по-другому из следующих рассуждений. Поскольку любая спиновая функция для частицы со спином 1/2 (то есть любой двумерный столбец) является собственной функцией оператора , отвечающей собственному значению (так как квадрат вектора спина такой частицы имеет в любом состоянии определенное значение), то матрица оператора является диагональной, причем диагональные матричные элементы равны , то есть матрица оператора и есть матрица (15).

Свойства матриц Паули

А. Все матрицы Паули, как матрицы операторов физических величин являются эрмитовыми.

Б. Для всех матриц Паули выполнено условие , где 1 – единичная матрица. Это можно проверить непосредственно. Это утверждение есть следствие того факта, что квадрат проекции спина частицы со спином ½ в любом состоянии имеет определенное значение (т.к. есть две возможности для проекции спина +1/2 и –1/2, а квадраты обоих этих чисел – ¼).

В.

Г. Любая матрица (22) может быть представлена в виде: . Это связано с тем, что единичная матрица и три матрицы Паули () образуют полный набор матриц (2), так как пространство таких матриц четырехмерно – матрица определяется заданием четырех чисел, поэтому любые четыре линейно независимые матрицы будут образовывать базис в пространстве таких матриц).

Д. . В частности, , т.е. они антикоммутируют. Алгебра (так называют правила умножения матриц) очень простая - при перестановке матриц просто меняется знак их произведения.

Е. Поскольку матрицы Паули связаны с операторами проекции спина 7на координатные оси для них выполнены обычные коммутационные соотношения для операторов проекций момента на координатные оси

(двойка в этом соотношении связана с тем, что ).

8