- •1.Множество натуральных чисел n. Аксиомы Пеано
- •2.Независимость аксиом Пеано
- •3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
- •4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
- •5. Теорема о сложении натуральных чисел: единственность
- •6. Теорема о сложении натуральных чисел: существование
- •7.Ассоциативность сложения натуральных чисел
- •8. Коммутативность сложения натуральных чисел
- •Существование:
- •23. Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел
- •26. Свойства сложения и вычитания для натуральных чисел: .
- •27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. Степень натурального числа с натуральным показателем и ее свойства
- •28. Равномощные множества. Отношение эквивалентности «быть равномощным». Отрезок натурального ряда. Конечные и бесконечные множества
- •29. Теорема о равномощности конечного множества только одному отрезку натурального ряда
- •30. Лемма о наибольшем и наименьшем элементе в конечном множестве. Бесконечность множества натуральных чисел
- •31. Счетность множеств целых и рациональных чисел. Несчетность множества действительных чисел
- •32. Отношение эквивалентности на множестве n2. Определение целого числа как класса эквивалентности на n2. Примеры
- •33. Определение суммы целых чисел и его корректность
- •34. Свойство сложения целых чисел
- •35. Определение произведения целых чисел и его корректность. Кольцо целых чисел и его свойства
- •38. Вложение множества натуральных чисел в кольцо целых чисел. Множество положительных целых чисел: определение, корректность определения, описание
- •40. Целое число как разность двух натуральных чисел. Отрицательные и положительные числа. Архимедовость и дискретность кольца целых чисел
- •41. Определение рациональных чисел как классов эквивалентности
- •42. Определение суммы рациональных чисел и его корректность. Аддитивная абелева группа рациональных чисел
- •43. Определение произведения рациональных чисел и его корректность. Поле рациональных чисел.
- •46. Вложение кольца целых чисел в поле рациональных чисел. Изоморфизм колец
- •47. Рациональное число как частное двух целых чисел. Поле рациональных как наименьшее поле, которое содержит кольцо целых чисел
- •49. Представление бесконечных периодических десятичных дробей обыкновенными дробями: правило, примеры
- •50. Определение действительных чисел как бесконечных десятичных дробей. Множество конечных десятичных дробей. Подходящие дроби
- •51. Определение и свойства отношения порядка на множестве действительных чисел
- •52. Плотность множества д в множестве действительных чисел
- •53. Определение и свойство суммы и произведения действительных чисел. Поле действительных чисел и его свойства
- •54. Определение, свойства и алгебраические операции с комплексными числами
- •55. Определение кватернионов. Алгебраические операции над кватернионами. Тело кватернионов
- •56. Вложение поля комплексных чиселв тело кватернионов. Теорема Фробениуса
38. Вложение множества натуральных чисел в кольцо целых чисел. Множество положительных целых чисел: определение, корректность определения, описание
Определение:
Будем говорить, что целое число
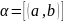 положительное, если а>b.
И будем обозначать
положительное, если а>b.
И будем обозначать
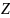 +
-
множество всех положительных целых
чисел.
+
-
множество всех положительных целых
чисел.
Свойство1: (корректность определения) Определение корректно.
Доказательство:
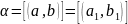 ,
a>b
,
a>b
доказать:

(a,b)
~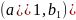 : a+
: a+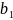 =b+
=b+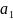 ,
a>b
,
a>b
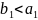 .
.
Лемма1: Множество +={[1+k;1]| k }
Доказательство:
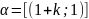 ,1+k>1
,1+k>1
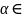 +
+
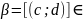 +
c>d
+
c>d
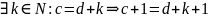
(c;d) ~ (c+1;d+1)=(d+k+1;d+1) ~ (k+1;1).
Свойство2:
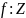 +
+
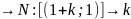
Доказательство: k≠n [(1+k;1)]≠[(1+n;1)] – отображение и иньекция
[(1+n;1)].
39.
Биекция
+
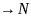 сохранение
отношения «>», суммы и произведения.
Отображение f-1
как
вложение N
в Z
сохранение
отношения «>», суммы и произведения.
Отображение f-1
как
вложение N
в Z
Теорема1: Отображение + сохраняет отношение «больше чем», «сумму», «произведение».
Доказательство:
α>β
 f(α)>f(β)
f(α)>f(β)
α= [(1+k;1)] β=[(1+n;1)]
α>β (1+k)+1>1+(1+n) k+2>n+2 k>n
f(α)>f(β)
f(α+β)= f(α)+f(β)
α= [(1+k;1)] β=[(1+n;1)]
α+β=[1+k+1+n;1+1]=[(1+k+n;2)]
f(α+β)=k+n= f(α)+f(β)
f(αβ)=f(α)f(β)
α= [(1+k;1)] β=[(1+n;1)]
αβ=[((1+k)(1+n)+1;1+k+1+n)]=[(1+kn;1] f(α*β)=k*n= f(α)*f(β).
Следствие:
Отображение f-1: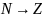 +
:k
+
:k [(1+k;1)]
является инъекцией сохраняет сумму,
произведение и отношение «>».
[(1+k;1)]
является инъекцией сохраняет сумму,
произведение и отношение «>».
Таким
образом f-1
является вложением
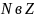 и позволяет нам рассматривать
как
подмножество в
.
и позволяет нам рассматривать
как
подмножество в
.
40. Целое число как разность двух натуральных чисел. Отрицательные и положительные числа. Архимедовость и дискретность кольца целых чисел
Свойство 1(архимедовость кольца целых чисел): ,, >0 n N:n>
Доказательство: >0 ,N
0 n=1
Свойство 2(дискретность множества целых чисел): каждое целое число имеет соседнее число +1, т.е. не : <<+1
Доказательство: N +1=’N, для натуральных чисел дискретность была доказана
N (-)
00
f:N{0}{-N}{0}: -
Далее рассуждаем от противного: если бы для отрицательных чисел выполнялось –(+1)<-<-, то тогда бы т.к. f биекция<<+1 ?!
Нет натуральных чисел между 0, 1 и -1,0
Нет натуральных чисел перед 1 поэтому не существует натурального числа между 0 и 1.
-1, 0 – не существует отрицательного целого числа - между -1 и 0.
Свойство 3:
>+>+
> >+>+
>>0>
>->0
=0=0=0
Доказательство:
=[(a,b)], =[(c,d)] , =[(m,n)]
>a+d > b+c
+=[(a+m; b+n)]
+=[(c+m; d+n)]
Доказать: +>+
a+m+d+n> b+n+c+m
a+d>b+с
>
Свойство 4: Множество целых чисел счетно.
Доказательство:

41. Определение рациональных чисел как классов эквивалентности
Определение:

Пара
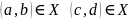 ,
если ad=bc
,
если ad=bc
Теорема 1: Отношение « » таким образом, определенное является отношением эквивалентности.
Доказательство.
1) Рефлексивность:
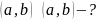
2)
Симметричность:
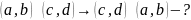
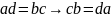
3)
Транзитивность:
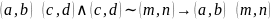

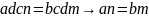
Свойство
1:
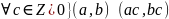
Доказательство: abc=bac
Следствие:
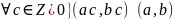
Доказательство: симметричность относительно « »
Определение: рациональными числами будем называть классы эквивалентности
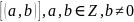
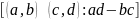
Обозначения: